移动质量速度对钢轨动力响应的影响*

黄志辉，陈庆广，李屹罡，施亮林

(1.中南大学 机电工程学院，湖南长沙 410083;2.中南大学高性能复杂制造国家重点实验室，湖南长沙 410083)

在轮轨相互作用的轨道监测现场，列车以不同的载重量以及不同的速度通过轨道时，由于速度的影响，车轮对轨道会产生扫掠力［1］的作用。在轮轨系统的动力学分析与研究中，钢轨的受力变形问题一直是研究中的重点之一。移动载荷实验研究中，发现移动车辆速度的不同引起监测结果的变化，针对这一现象，本文通过实际钢轨的振动力学模型的理论上分析钢轨变形与移动车辆速度之间的规律，并通过实验对其进行了验证。

1 实验台轮轨系统力学模型的建立

现有的监测实验台由上轨道、小车、下轨道、弹性支撑及轨道固定架5个部分组成，上轨道在小车的运行过程中只起导向作用，在研究中将小车的运行简化为小车在下轨道上行驶。虽然连续弹性支撑梁模型求解方便，可以得到解析解，但难以反映轨枕间断支撑效应、轨枕失效及支撑刚度不均匀等问题，而弹性点支撑模型的功能比较强大，计算结果更接近实际情况［2］，本文在轨道振动分析中采用这一模型。整个轮轨系统简化后的模型如图1所示。

图1 轮轨系统力学模型Fig.1 Mechanical model of wheel/rail system

与简支梁振动不同的是，钢轨在弹性点支撑位置处，需要考虑弹性支撑阻尼和刚度系数的影响，钢轨的振动方程为［2］

其中:EI为梁的抗弯刚度;w(x，t)为t时刻简支梁x处的动挠度;m为单位长度梁的质量;M为小车质量;xp为小车所在的位置坐标;δ为狄拉克函数;N为一段轨道内轨道的支撑点个数;Fj为第j个支撑点的轨枕支撑力。即

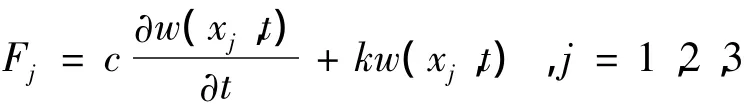
其中:xj为轨枕支撑点位置;k和c分别表示弹性支撑的刚度和阻尼。

关于钢轨振动的求解一般采用模型离散方法，包括振型叠加法即振动模态法、有限元法和传递矩阵法3种［2］。对于结构振动问题，振动主要由频率较低的前几阶基本振型构成［3］，在与其他2种方法的比较中，振型叠加法可以依据所分析的频率区段来选择合理的钢轨自由度，降低系统自由度，简化计算，提高求解效率，避免车辆与轨道之间耦合力的计算，同时还具有较高的计算精度［2］，因此本文采用振型叠加法来对振动方程(1)进行求解。

用振型叠加法将梁振动的动位移写成各振型的叠加并分离变量［4］:

其中:φi(x)为梁的第i阶振型(模态)，图1所示的模型中，设钢轨的各阶振动模态仍与简支梁模型相同，则有 φi(x)=sin()［5］;qi(t)为与 φi(x)相对应的广义坐标，也就是模态响应。

本文主要分析与论证匀速运动小车对轨道变形的影响规律，所以取xp=vt，将φi(x)和qi(t)带入钢轨振动方程求解，整理得

其中mi=(m+M)∫l0φi(x)φi(x)dx

2 模型参数的确定及速度影响分析

监测实验台的实际轨道参数如表1所示，结合轨道参数对方程式(3)进行求解。

表1 轨道的计算参数Table 1 The calculation parameters of the rail

在对钢轨的振型进行叠加时，发现钢轨的振动取到前7阶时已经趋于平稳，本文只取振型的前7阶进行叠加，即取n=7，此时所得到w(x，t)的值可以基本上模拟出钢轨的振动情形，而不影响本文的分析研究。

结合监测实验台的小车行驶速度，选取移动小车的速度分别为10，30，50和70 km/h 4种工况，运用MATLAB对钢轨的动力响应进行仿真分析。选取图1所示的A点即x=1.265 m处钢轨在不同速度下的动力响应如图2所示。

图2 不同速度下A点处钢轨的动力响应Fig.2 The rail’s dynamic response of A point under different velocities

由图2可得，当移动小车以不同的速度从钢轨上通过时，在x=1.265 m位置处点的动力响应规律一致:先是趋于平稳，之后迅速增大到一点，接下来迅速减小，最后又趋于平稳，这种现象符合力学规律。结合图2中不同速度的工况下钢轨的动力响应幅值可得到移动小车速度与钢轨动力响应的规律:钢轨的动力响应随着小车速度的增大而减小。

3 实验对比分析

针对理论所得到的速度与钢轨变形之间的规律，运用监测实验台对小车在不同速度下钢轨的变形规律进行实验验证。在监测实验台上，分别在x=1.265 m 和 x=1.485 m 2 点(参图1 中的 A、B)处且对称于钢轨中性层的四个位置粘贴半导体应变片，组成全桥电路，采用数据采集板卡对小车通过钢轨时钢轨的动力响应进行采样并将信号进行放大输出，将钢轨的动力响应即应变变形转换成电压信号进行分析。

在对钢轨的变形信号进行采样时，调整采样初始电压为+3 V，采样频率为30 000 Hz。通过实验，不同速度下采样得到的钢轨响应变形趋势总是一致，图3所示为10 km/h和70 km/h钢轨的变形趋势图。

图3 两种速度下钢轨的动力响应Fig.3 The response of rail under two different velocity

在应变片粘贴的位置处，钢轨产生的变形最大，图2中仅为一点的动力响应，而实验所得的信号曲线是2点处响应的叠加，所以在钢轨的动力响应波形中含有2个波峰;为了验证速度与钢轨动力响应的规律，针对不同速度下钢轨的动力响应波形，对2个波峰间的动力响应值求平均并对其进行2次拟合，得到如图4所示的规律:随着小车移动速度的增大，钢轨的动力响应逐渐减小。

图4 钢轨的动力响应随速度的变化Fig.4 The dynamic response of rail with the changing speed

4 结论

(1)采用求解振动方程的形式研究钢轨的动力响应随移动质量速度变化规律的方法是可行的;

(2)随着移动质量速度的增大，钢轨的动力响应逐渐减小;

(3)实验结果与仿真规律具有一致性，证明了移动小车的速度提高导致钢轨的动力响应减小，从而小车的监测重量值变轻。

［1］黄志辉，申文静.高速车轮扫掠力监测系统的集成研究［J］.北京:现代制造工程，2009(6).1 －3.HUANG Zhi-hui，SHEN Wen-jing.Integrate study on a wheel－scan force monitoring system for high speed wagon［J］.Beijing:Modern Manufacturing Engineering，2009(6):1－3.

［2］刘学毅，王 平.车辆－轨道－路基系统动力学［M］.成都:西南交通大学出版社，2010.LIU Xue-yi，WANG Ping.Vehicle track subgrade system dynamics［M］.Chengdu:Southwest Jiao Tong University Press，2010.

［3］ Clough R W，Penzien J.Dynamics of Structures［M］.McGraw － Hill Inc，1975.

［4］赵晓华，张谢东.移动车辆荷载作用下简支箱梁动力特性的数值分析［J］.武汉理工大学学报，2011，4(2):349－352.ZHAO Xiao-hua，ZHANG Xie-dong.Numerical analysis on the dynamic characteristics of the simple－supported box － girder under moving vehicle loads［J］.Journal of Wuhan University of Technology，2011，4(2):349 －352.

［5］欧珠光.工程振动［M］.武汉:武汉大学出版社，2003.OU Zhu-guang.Engineering vibration［M］.Wuhan:Wuhan University Press，2003.

［6］杨岳民.车桥耦合振动问题的振型叠加法求解［J］.中国科技论文在线精品论文，2011，4(2):155－160.YANG Yue-ming.Mode － serposition solution of coupled vibration between vehicle and bridge［J］.Chinese Science and Technology Papers Online Boutique Papers，2011，4(2):155－160.