隧道爆破振速小波包及数值模拟对比分析*

曹 琦，傅鹤林，王松周，刘运思

(中南大学土木工程学院，湖南长沙 410075)

对于爆破振动速度衰减规律的研究，工程中主要采用苏联学者萨道夫提出的经验公式V=对实测数据进行拟合，得到衰减公式。但此经验公式无法准确地体现场地特征对衰减的影响，也无法分辨场地对不同频率波的不同衰减作用，因而在应用衰减公式预测非测点爆破振速时，得到的结果不够准确。国内不少学者将小波包变换引入到爆破震动研究中，利用小波变换将爆破震动信号在时域、频域上展开，根据不同的频带的地震波对结构的危害程度取加权系数，将地震波信号在各个频带上的主震相的能量按加权系数合成，提出了用合成后的能量值作为爆破地震危害程度的判据。

数值分析可采用不同地层参数的模型，有效地体现围岩特征对振速衰减作用的影响。小波包分析则从频率这个角度出发，将复杂的爆破振动信号分解成不同频段的振速波，进而可以研究场地对不同频段波的衰减影响。

本文拟运用数值模拟和小波包分析方法，对一组实测振动数据分别进行模拟和分析，并对非测点数据进行预测，力求得到较为合理的预测值。

1 数值模拟

1.1 爆破荷载的确定

对于爆破振动的模拟，难点主要在于爆破荷载的计算，目前大部分研究都是针对单孔爆破，实际隧道开挖过程中，往往是多段多孔爆破，本文采用国际上惯用的爆破荷载模式［1－3］:

式中:P'max为多孔爆破峰值荷载;f(t)为时间滞后函数，取指数型表达式:

当 f(t)=1.0，t=tr时，可得 Ptr计算公式:

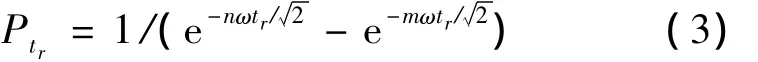
式中，tr为爆破冲击波起始作用时间，计算公式为:

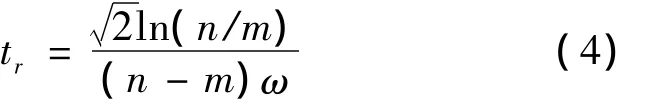
式中:n，m为阻尼系数，取决于爆破冲击波起始作用位置和波形;ω为振动频率，取决于岩体的纵波波速Cp和药孔直径Db，按下面公式计算:

由波动理论:

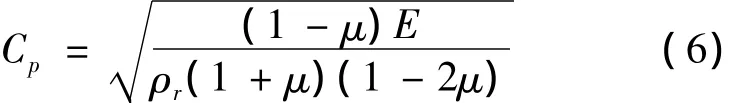
式中:μ为岩石的泊松比;ρr为岩石的密度;E为岩石的弹性模量。

爆破冲击波在炸药与岩体界面上给予岩体的最大荷载与岩体特性有关:

式中:Pmax为单孔爆破在岩石表面产生的峰值荷载;V为炸药的爆速;ρ0为炸药的密度;P0为最大爆炸荷载，耦合情况下

炮孔内的冲击波作用在岩石圈上的峰值荷载随着距离而衰减，第n个炮孔的单孔爆破峰值荷载随着距离变化的衰减关系如下:

式中:rn为计算点离爆孔的距离;rb为药孔半径，是爆破峰值荷载衰减系数，按公式α=2+μ/(1－μ)计算。

爆轰波在岩石中以波的形式传播，因此这里按波的叠加规律，将各个炮孔产生的爆破峰值荷载叠加，求得作用在爆心的爆破峰值荷载，即P'max=。波的叠加取决于波速、频率、相位及空间传播方向等，而炸药类型、药量、装药方式、钻孔深度、钻孔角度、钻孔直径、钻孔布置相对位置、起爆时间、场地特征等都会影响波的叠加。本文中近似认为同一断面各个炮孔炸药类型、药量、装药方式、孔深、孔角、孔径一致，并假定隧道处于同一种围岩中。采用微差爆破时，只需选用最大段药量产生的峰值荷载［4］。

图1为某隧道III级围岩上台阶(三台阶)开挖炮眼布置。使用2号岩石乳化炸药，其爆速为3 000 m/s，炸药的密度为 1 g/cm3，炮眼直径为 0.04 m，孔深 2 m，根据文献［4］，取阻尼系数 n=0.055，m=0.035。此处围岩为板岩，其岩石力学参数见表1。

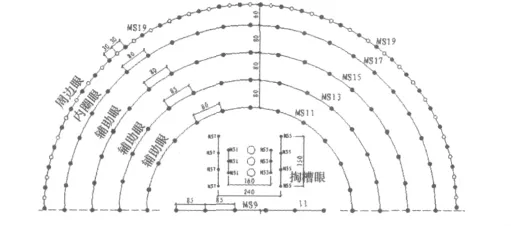
图1 III级围岩上台阶(三台阶)开挖炮眼布置图Fig.1 III class rock on the steps(three steps)excavation bore hole layout

表1 岩石物理力学性质Table 1 Physical and mechanical properties of rock

由以上8个参数，求得:

Pmax=3.52 GPa，α =2.3，rb=0.02 m。再根据炮眼布置图求得最大段MS5的峰值荷载:

爆破中心处的爆破荷载随时间的表达式为:P(t)=10.95 × (－6.07)× (e－3718t－ e－2367t)GPa爆破荷载随时间的历程如图2所示。

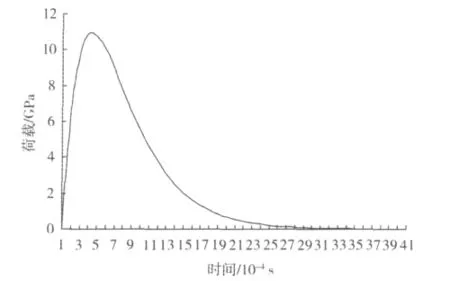
图2 爆破荷载时间历程Fig.2 Blast loading time history

1.2 模型建立

为了获得地层振动特征值，先进行特征值分析，在这个过程中使用曲面弹簧来定义弹性边界。根据获得的振动特征值，再重新定义模型的边界条件，施加爆破荷载，进行爆破振动时程分析。从结果中可以提取测点振速。每一次爆破都独立进行模拟，从而可以分别得到不同次爆破下测点的振速，模型如图3。由数值模拟得到的爆破峰值振速模拟值见表2。

图3 模型图Fig.3 Model diagram

1.3 数值模拟结果

由数组模拟得到的爆破峰，振速模拟组见表2。

2 小波包分析

2.1 爆破振速实测数据

现场实测的爆破振速如表3所示。

2.2 小波包理论

小波包理论是在小波理论的基础上发展而来的，能够对小波分析中的高频部分进一步分解，并能够根据被分析信号的特征，自适应地选择相应频段，使之与信号频谱相匹配，从而提高时频分辨率。

表2 爆破峰值振速模拟值Table 2 Blasting simulated peak velocity

表3 各测点随距离变化的实测峰值振速及频率Table 3 Measuring points changes with distance and frequency of the measured peak velocity

因而应用小波包对地震波信号进行频谱分析，可以得到更为精准的信息。若存在数列{hk}，使得函数族{μk}可以由以下方式构成:

则称函数族{μk}为一小波包。

特别的，当n=0时，有正交小波函数μ1(t)及对应尺度函数μ0(t)使得:

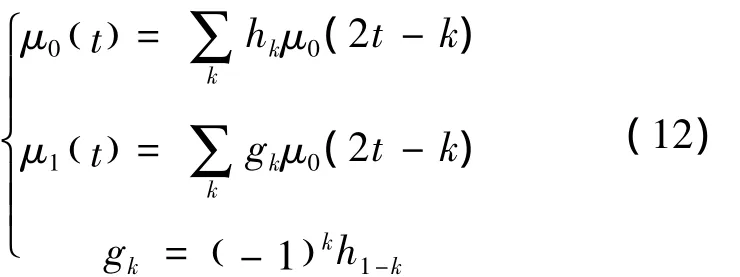
由此可知，函数族 {μk(t) }是由尺度函数μ0(t)确定的小波包。

利用式(11)和式(12)可以得到如下空间分解:

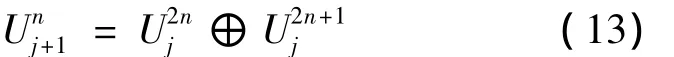
这样的分解过程，信号的高频部分也能像低频部分一样分解成2部分，从而得到比一般小波分析更精细的解。

2.3 小波包系数峰值衰减规律

爆破地震波在围岩中传播时，不同频率范围的地震波分量衰减程度是不一样的，这种衰减反应了爆源和场地特征。为了研究爆破地震不同频率段波在介质中的传播规律，必须将不同频率段地震波信号从总信号中提取出来。应用小波包技术提取出不同频段的地震波分量，然后再逐一分析各分量振动衰减规律与距离、药量的直接关系，在此基础，对所有频段峰值速度的衰减规律进行归一化处理，就可以得到预测非测点处振动峰值速度的公式［5－7］。图4为第1次爆破中测点1地震波采用‘db5’小波分解后，频带为16～64 Hz的小波包系数峰值与折算距离的关系。这表明各小波包信号的振动衰减规律仍然满足萨道夫经验公式。

由表3可以看出，第1次爆破中，各测点爆破地震波频率主要集中在45～50 Hz，70～80 Hz以及100～110 Hz，根据小波包分析的二分法原则，研究本次信号时，主要采用16 ～64 Hz，64 ～96 Hz，96 ～128 Hz和128～160 Hz 4个频段。表4给出了以上各频段振动效应与比例距离的衰减系数以及之间的拟合相关系数。

图4 16～64 Hz小波包系数峰值与折算距离的关系Fig.4 16 ～ 64 Hz wavelet packet coefficients of the relationship between the peak and converted from

2.4 建立在小波包系数峰值基础上的爆破地震波预测

为了预测相同爆破条件下的爆破振动在某测点处的振动峰值波速，必须综合各频段的地震波衰减规律。这里采用如下公式进行:

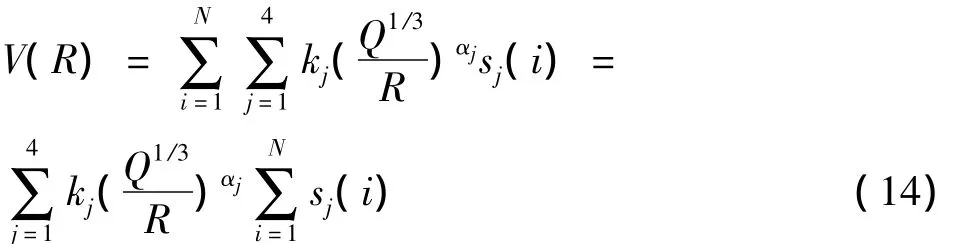
其中:j为频段序号，这里分为4个频段;i为原始信号点的序列号;sj(i)为第j频段第i信号点的小波包系数。

在进行振动峰值波速的预报时，先选取小波包各频段的系数sj(i)，对其中的最高峰值归一化处理。然后才能采用式(14)对距离为R处峰值波速进行预报。

表4 各频段振动效应衰减参数Table 4 The effect of attenuation of the vibration frequency parameters

2.5 小波包分析结果

小波包分析结果汇总见表5。

3 对比分析

由图5可知，小波包预测的测点爆破振速与实测值吻合较好，而数值模拟振速在离爆源60 m范围内均大于实测值，这是因为计算爆破振动峰值荷载时，是直接将各炮孔爆破产生的振动荷载峰值相加，从而导致计算的峰值荷载较大。并且在模型中加荷载时，是直接加在开挖后的隧道内表面，而很多爆孔产生的爆破冲击波到达隧道内表面时已经衰减成应力波，应力波的值要小于冲击波，因此这也是导致模拟振速大于实测值的原因。随着距离的增大，当距离超过60 m时，模拟值与实测值趋于一致，这是因为爆破荷载衰减很快，峰值荷载的影响时间很短，所以当距离较远时，地层对波的衰减作用很明显，从而弱化了峰值荷载偏大对振速的影响。

表5 基于小波包分析的爆破振速预测值Table 5 Based on wavelet packet analysis of the predictive value of blasting vibration velocity

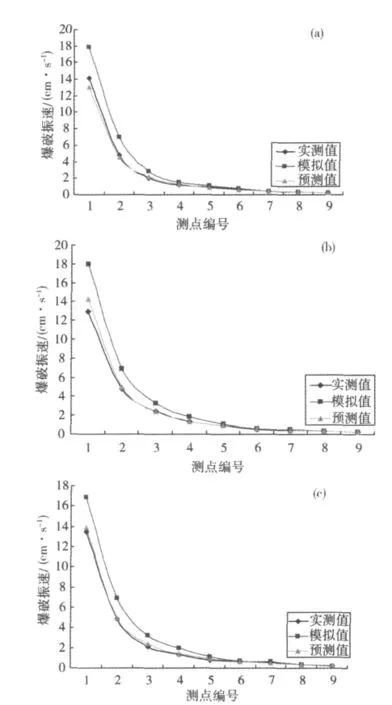
图5 爆破振速对比图Fig.5 Comparison chart blasting vibration velocity

4 结论

(1)目前，对于爆破振动荷载的计算大部分是建立在单孔或者单段爆破模型的基础上，所以用波的叠加理论建立全断面所有爆破段的爆破模型比较困难，从而导致数值模拟结果不够准确。

(2)当距离超过60 m时，基于小波分析的爆破振速模拟结果与实测值基本吻合，表明地层对爆破振动的衰减作用明显。

(3)基于小波包的爆破振速预测考虑了地层对不同频段波的影响，从而得到了与实测结果较为吻合的结果。

［1］石洪超，丁 宁，张继春，等.爆破动力作用下小净距隧道围岩振动效应分析［J］.爆破，2008，5(1):74－78.SHI Hong-chao，DIN Ning，ZHANG Ji-chun，et al.Analysis of vibration effects on surrounding rock for small clear distance tunnel under the dynamic action of blasting［J］.Blasting，2008，5(1):74 －78.

［2］Dowding C H，Aimone C T.Multiple blast－ hole stresses and measured fragmentation ［J］.Rock Mechanic and Rock Engineering，1985(18):17 －36.

［3］ Rathore S S，Bhandari S.Controlled fracture growth by blasting while protecting damages to remaining rock［J］.Rock Mechanics and Rock Engineering，2007，40(3):317－326.

［4］荣 耀.公路隧道爆破荷载的计算分析［J］.公路交通技术，2005(1):91－94.RONG Yao.Calculation and analysis of explosion loading of highway tunnels［J］.Technology of Highway and Transport，2005(1):91 －94.

［5］徐学勇.爆破震动信号的小波分析方法研究［D］.武汉:武汉理工大学，2006.XU Xue-yong，Study on wavelet analysis method for blasting seismic signals［D］.Wuhan:Wuhan University of Technology，2006.

［5］刘 辉，李波，吴从师，等.岩溶隧道掘进爆破震动效应分析［J］.长安大学学报:自然科学版，2010，30(4):56－59.LIU Hui，LI Bo，WU Cong － shi，et al.Analysis on effects of vibration resulted from driving blasting in Karst tunnel［J］.Journal of Chang’an University:Natural Science Edition，2010，30(4):56 －59.

［6］何本国，朱永全，张志强，等.超小净距隧道不同爆破方式现场试验研究［J］.铁道科学与工程学报，2010，7(5):65－ 65.HE Ben-guo，ZHU Yong-quan，ZHANG Zhi-qiang，et al.Study on in－situ test for different blasting methods of the super small－ distance tunnel［J］.Journal of Railway Science and Engineering，2010，7(5):65－ 65.

［7］林从谋，杨林德，崔积弘，等.浅埋隧道掘进爆破振动特征研究［J］.地下空间与工程学报，2006，2(2):276－279.LIN Cong-mou，YANG Lin-de，CUI Ji-hong，et al.Study on the vibration characteristic of the shallow－tunneling blasting［J］.Chinese Journal of Underground Space and Engineering，2006，2(2):276 －279.

［8］周志强，易建政，王 波，等.控制爆破技术研究现状及发展建议［J］.矿业研究与开发，2010，30(3):103－108.ZHOU Zhi-qiang，YI Jian-zheng，WANG Bo，et al.Present situation and suggestions of research and development of controlled blasting technology［J］.Mining Research and Development，2010，30(3):103 －108.