蒙皮约束下的动画角色模型分割方法

李 琳， 谢文军， 刘晓平

（合肥工业大学计算机与信息学院可视化与协同计算(VCC)研究室，安徽 合肥 230009）

模型分割技术是计算机图形学中几何处理的一个关键问题，它是很多应用和研究工作的基础，包括三维检索与建模、网格变形、网格压缩和简化、纹理映射、骨架提取与动画生成等。由于它是一个很重要的共性问题，所以研究工作自90年代以来从未间断。国内外近几年都有综述性文献对它进行广泛而深入的探讨和展望[1-3]。Ariel Shamir[2]将网格分割分为块分割和部件分割两种情况，认为部件分割均需要产生有意义的结果，因而部件分割大都基于人类感知利用其结构性分解为语义部件。部件分割有一个重要的应用目的是基于实例的建模[4]，就是从已有的三维模型中分割出所需要的部件用来替换正在制作模型的同样部件。

在游戏和电影电视动画中经常使用的三维角色模型制作周期长，样式单调，且现有的复杂建模工具难以对角色模型的部件进行重用，参考基于实例的建模方式，角色模型的分割是进行三维角色模型快速复用，从而提高建模效率，丰富角色多样性的首要解决问题。由于模型分割的应用面非常广泛，从而导致了面向不同的应用所采用的技术与方法众多，Ariel Shamir在文献中列举了 10种技术以及在技术中可以称之为参考的16种特征属性[2]。在游戏和影视动画中经常使用的三维角色模型除了三维网格，设计师还必须为角色设计用于动画的骨骼，并建立起网格模型与骨骼之间的关联——蒙皮信息，相比于只从三维网格上寻找分割特征属性的技术，角色模型有着额外适合分割的语义特征属性——骨骼和蒙皮，但由于其特殊的应用领域与构成要素，使得没有研究关注此类模型的分割问题。但是在 Ariel提到的模型分割技术中，有一类基于骨骼特征或运动序列的分割在利用骨骼语义的想法上有着相似性，即认为动画中运动属性相似的点应该属于一个语义部件。文献[5]通过拓扑相似求解出基本的骨架线，然后使用与骨骼垂直的连续截面扫掠三维模型表面，产生顶点分割以达到模型分解为语义部件的目的；文献[6]对一段给定模型的运动序列进行主成份分析给出统一表示，然后匹配顶点间运动相关性，考察相似度来分割模型顶点。这些方法因为只具有三维模型信息，因此求解骨架或运动关联度非常困难，而且对模型的复杂性以及骨架的清晰度也有一定的要求；而动画角色模型的自身属性为各种复杂模型的分割创造了优厚的先天条件，适应性更强。

本文针对游戏和三维动画中已经存在的三维角色模型，提出一种在蒙皮信息约束下的模型分割技术，通过已知的骨骼语义与约束，查找相应的蒙皮信息，确定属于某个语义部件的几何数据，并根据一定的拓扑约束和分割规则对该数据进行调整和优化。与之前各类型的自动分割方法比较，本文方法简单易用，适应性强，但要求处理的对象是完整的角色模型。在实际应用中，此类模型是游戏与动画的基础，拥有大量的数据来源，本文的研究内容即来自一个游戏角色建模中的项目，将不同的角色通过分割重组为一个新的角色，从而加快建模速度，提高建模效率。

1 形式化表示与算法框架

文献[2]中将模型分割总结为一个最优化问题，将分割对象描述为一三元组M= ＜V,E,F＞（其中V——顶点、E——边、F——面片），分割即是寻找使得判定条件J最大或者最小的几何元素集合S，使得S可以分割出M的子集M' = ＜V',E',F'＞。由于传统模型分割算法仅是针对静态三维网格模型，因此点、边、面表示方法已经足够，但是对于游戏与动画中使用的三维角色模型，还存在着骨骼和蒙皮信息，因此描述需要扩充到五元组。

定义1角色模型C被定义为一个五元组C= ＜V,E,F,B,SK＞，其中顶点V= {pi|pi∈R3,1≤i≤m}，边骨骼且三维模型为三角化封闭网格，除重心外任一骨骼仅有一关联骨骼，蒙皮正确完整。

本文采取根据骨骼语义信息来选择分割后的顶点集合，由于每个顶点i受各骨骼j影响的蒙皮约束信息ijr有所不同，需要给出一定的权值判定条件1J；由于三维部件模型拓扑约束关系，需要给出一定的条件限制2J；为了将分割出的模型利于组合，需要给出优化规则3J。

定义 2角色模型C分割是一个最优化问题，给出一个角色C与骨骼语义信息集合B' ，找到一个顶点集合V'可以将C分解为1C与2C两个角色部件，并同时满足条件规则集合

定义 3 角色部件pC也是一个五元组＞，其每一项都是被分割的源角色C的子集，且 ＜Vp,Ep,Fp＞构成的三维模型符合三角化要求，不封闭但仅有一个缺口，任一骨骼仅有一关联骨骼，蒙皮正确完整。

角色部件可以作为部件信息保存下来，并且因为是一个完备的集合，可以多次使用。由上述定义及描述可以给出本文模型分割技术的算法框架，如图1所示。

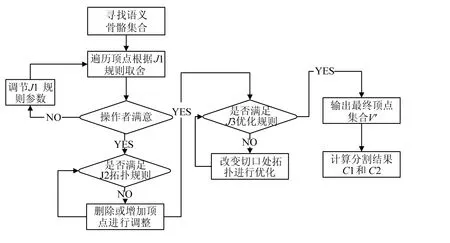
图1 本文算法框架

2 基于骨骼与蒙皮的预分割策略

2.1 子树选择法

骨骼是动画角色的重要构成部分，与三维网格模型相比，它带有明显的语义特征，骨骼间有着从属关系，通常用树来表示，如图 2[7]，立方体线框表示犀牛的骨骼，左边是所有骨骼所代表的树。每一个BONE是树节点，表示为：

图2 骨骼树的从属关系

骨骼的名字代表了角色的某个部件的一部分，比如Thigh表示上腿骨、Tail表示尾巴根。在角色部件的分割中，往往需要切割出更大程度的语义所表示的部件，比如下肢，则需要上腿骨、下腿骨、脚掌、脚趾等骨骼所代表的部分总集，如图2中的白色矩形表示的范畴。在骨骼的层次关系中，其父子关系反映了动作相关性，具有相关性运动趋势的顶点可以认为是代表了一定语义范畴的部件概念，因此，当用户给出一个骨骼语义，可以以该骨骼为根结点搜索该子树上所有结点并加入到骨骼选择集合中，从而找到该骨骼所联动或代表的语义部件。搜索骨骼集合B'可以采用树的深度遍历算法。算法描述如下：

2.2 蒙皮权重对选择顶点的影响

蒙皮(SKIN)是一种模型顶点受骨骼影响而产生动画的技术，受骨骼影响程度越明显的顶点i相应于这个骨骼j的蒙皮约束信息ijr就越大，关节处往往受到上下两根骨骼的影响，如图3所示，受上腿骨影响的顶点颜色越偏蓝色调代表蒙皮值越小。蒙皮数据SK=（其中i是顶点数目，j是骨骼数目）是一个庞大的稀疏矩阵，可以从其第j列找到受j骨骼影响的所有顶点，由于影响权重不同，因此挑选规则成为影响分割取舍的重要参数化约束条件；由于每次搜索到的骨骼集合一般不止一个骨骼j，因此对于顶点i计算新权重)，相应的规则变为J1:ri≥R。初始R值可以采取折半方法取50，根据调节R值来寻求一个较为满意的区域结果，但并不一定存在完全正确和最优的解。

图3为根据上腿骨找犀牛相关顶点所产生的结果。可以发现，选择后的顶点集合一般并不符合角色部件的拓扑条件，多数情况下有可能有孤立点、孤立线（如图3）、孤立面；或者即使连通也是低连通，其中会有桥[8]；如果切割产生了多个缺口（下文称缺口环），则给后来使用这个部件再组合新角色制造了一定的困难，这时就需要在预分割的基础上进行顶点求解与优化，使之满足拓扑约束，并且能够减少缺口环，使分割口尽量规则圆滑。

图3 骨骼选择顶点的结果

3 拓扑规则与优化目标

3.1 拓扑约束

为了对预分割后的顶点集合进一步处理，可以将该顶点集合V'构成的三维网格看作一三元组M' = ＜V',E',F'＞ ，边集E' = {eij|eij∈E∧i,j∈V'}，面集F' = {fijk|fijk∈F∧i,j,k∈V'}。该网格必须满足定义 3中对角色部件的拓扑规则J2：所有顶点连通，每个点都是三角面片的顶点，不封闭但仅有一个缺口环。

三维网格是全封闭的必要条件是每一条边都被两个面所拥有，那么在预分割后的三维网格中出现的只在一个面上的边或者没有面包含的边都是由于网格分离而造成的，因此很容易检测出没有封闭的切口处，如果切口处恰巧是一个头尾相连的环，那么切口是满足拓扑要求的，否则认为切口出现了孤立点、线、面、桥或多个环的可能性，如图4所示。由于蒙皮信息的连续性，一般是延着环状切口向外延伸出现少量孤立或由桥连接的点集，或者切割到一些突起或凹陷的部分而产生多余缺口环。针对这种特点，在将切口处的顶点和边转化为图 (, )G V E后，用以下算法来解决这一问题，主要是去除多余点集，并修补多余产生的缺口环，其中检测桥与连通集算法使用文献[8]中的图的深度遍历，而修补网格缺口的算法采用文献[9]中的最小二乘网格修补算法，由于在切割过程中形成的多余缺口都非常小也没有孤岛现象，所构造的矩阵也很小，因而计算也不复杂。

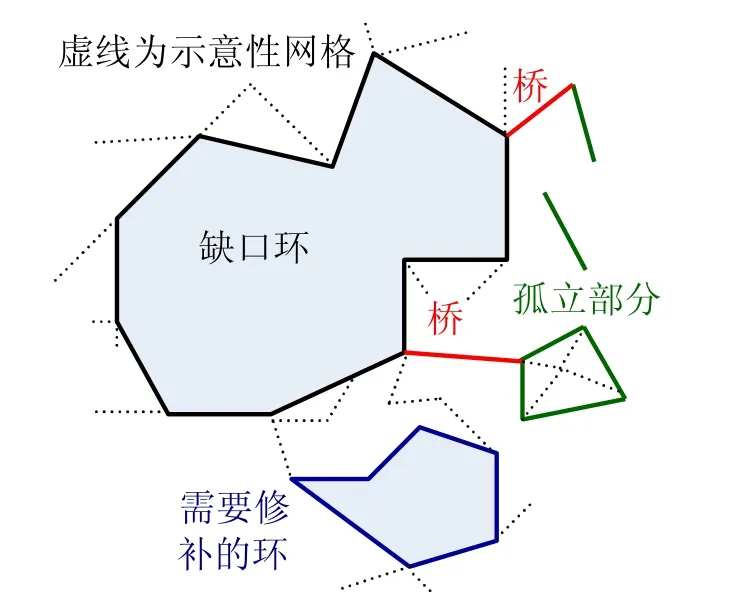
图4 切口处的可能性

Step 7与切口环在M'中连通的环为多余的缺口环，因此修补之。

采用切口部分进行预先判断调整，避免了采用整个M'作为图来处理的复杂性。通过以上处理，缩小了顶点集合V'的范围，由此产生的新三维网格M' = ＜V',E',F'＞已具备了构成定义 3中角色部件的网格拓扑条件，可以达到分割的要求了。

3.2 优化目标

为了满足角色部件模型的重组连接，希望三维网格的缺口环比较规整圆滑，文献[10]对网格分割结果提出了一种一般化的优化方法，这种优化方法在面片上产生新折线，但该方法的效果与网格密度有非常直接的关系。在本文处理对象网格较稀疏的情况下，可以根据该文献提及的凹度最小原则，对3.1中产生的三维网格M'进一步优化。

图5 凸起和凹陷

如图5是经过J1、J2规则处理后的犀牛右后腿相关联的网格，可以发现明显的凸起和凹陷破坏了边缘平滑，对任意 3个连续的顶点(v1，v2，v3)考察其凹度，有以下3种情况需要调整：

1） 凹度>α度，v1v2v3形成边缘三角形，则为凸起，去除v2点可改善；(α>180)

2） 凹度<β度，v1v2v3不是三角形，则为凹陷，连接v1v3可改善；(β<180)

3） 凹度>β度，v1v2v3不是三角形，则考察连接v1v3后的新三角面与邻接面是否构成凸起。

因此提出优化规则J3为：缺口环上任意 3个连续的顶点 (v1,v2,v3)，不存在边e=v1v3使得缺口更平滑。将缺口环的顶点集合设置为Vjoint= (v1,v2…vn)，对相邻三点vi vi+1vi+2(i=1…n-2)进行判断并区分上述情况进行调整，由于去点或加边会使Vjoint发生变化，可能会有新的凸起和凹陷，因此该过程应该重复进行，直到没有调整情况发生。

上述调整规则中的α和β属于经验数据，在本文中经过大量测试认为α=240，β=150较好。

第3）种情况比较特别，因为在实际应用过程中经常出现切割到模型上局部凸起部位，融合后则应封闭这个区间。考察这部分因素，发现若连接v1v3后，新生成的三角面△v1v2v3与相邻两面的夹角较大，则认为该切口处面片不平滑有突起，则在M'中产生新边与三角形，使切口更紧密平滑；若夹角很小，一般认为<30度，则认为仍属于面片平滑过渡，不处理之。

该优化方法对平整有尖角凸起或凹陷的边缘比较有效，而对于边缘缓慢变化的趋势无法抑制，处理后的网格缺口环并不能完全接近一个平面，对于分割后的两个部件的融合提出了较高的要求，但平整尖角避免了重组时模型融合产生狭长三角面片，而且该方法当切割到模型上突起部位后会将之闭合，有利于后期的模型融合。

4 算法应用实例

将本文算法应用到几十个数据完备的动画角色部件的选择中，通过设计者指定关键骨骼，程序迅速找出其子骨骼并由蒙皮信息进行预分割，进而通过拓扑检查与优化得到分割结果，所费时间不超过0.1秒，如图6展示的不同动画角色的分割效果。测试对象与经过的规则如表1所示。

表1 测试对象与经过的规则

图6 动画角色切割结果

经过实际应用中的动画角色的测试，发现有70%到80%的部件选择只经过预分割就能很好的满足角色部件拓扑的要求，尤其是骨骼分明的昆虫和体型瘦弱的角色，而部件不分明的动画角色如体型肥大的角色在预分割后多数并不满足拓扑要求，需要进一步处理，而对于切口处的优化几乎90%以上的部件都会发生，对于切口处范围比较小的部件，通常在本文优化方法下切口会继续填补得更小，甚至通过优化产生闭合，如蚂蚁的腿、骨龙的翅膀。对于这种情况，可以设法动态改变β值；如果不可避免地被闭合，那么在使用该分割部件的时候需要注意，在本文相关项目所涉及的模型融合中，一般是以切口较大的模型作为融合参照，因此，无切口或者切口较小的网格部件在与相同模型融合时并无太大不同。

5 结 束 语

本文关注在影视动画与游戏行业中使用的动画角色的数据重用问题，针对三维网格分割这一计算机图形学领域的经典基础问题，立足于动画角色较之三维模型更丰富的数据信息，提出了一种基于蒙皮约束的模型分割方法，根据蒙皮信息预分割后，再进行拓扑判断与切口优化，产生符合模型重用要求的角色部件的三维网格。该方法已在与某游戏公司合作研发的动画角色部件组合系统中使用，其有效性和对动画角色的支持度得到了肯定，但同时，由于蒙皮制作的复杂，现代动画角色的三维网格顶点一般并不密集，而是通过各种纹理来表现其精细度，本文方法仅在该类对象上得到了充分验证，不能推广到其它无蒙皮的三维网格模型，但拓扑检查的方法与切口优化方案可以为其它网格分割算法所借鉴，其中，优化方案部分值得进一步研究和探讨，对于后期的模型融合来说，切口优化的最好效果为一标准圆环状结构。

[1]孙晓鹏, 李 华. 三维网格模型的分割及应用技术综述[J]. 计算机辅助设计与图形学学报, 2005, 17(8):1647-1655.

[2]Shamir A: A survey on mesh segmentation techniques [J].Computer Graphics Forum, 2008, 27(6): 1539-1556.

[3]Attene M, Kats S, Mortara M, et al. Mesh segmentation—— a comparative study [C]//Proceedings of the International Conference on Shape Modeling and Applications, Matsushima, Japan, 2006: 14-25.

[4]Funkhouser T, Kazhdan M, Shilane P, et al. Modelling by example [J]. ACM Transactions on Graphics, 2004,23(3): 652-663.

[5]Li X, Toon T, Tan T, et al. Decomposing polygon meshes for interactive applications[C]//Proceedings of the 2001 symposium on Interactive 3D Graphics(2001),2001: 35-42.

[6]Leet Y, Lin P H, Yans U, et al. Mesh decomposition using motion information from animation [C]//Proceedings of Computer Animation and Virtual Worlds (2005), 2005: 519-529.

[7]Autodesk, Inc. 3ds Max 8 Documentation [EB/OL].http://usa.autodesk.com/adsk/servlet/item?siteID=123112&id=9861621, 2010-3-31.

[8][美]Thomas H C 等. 算法导论[M]. 潘金贵, 等译.北京: 机械工业出版社, 2006: 322-340.

[9]周明东, 林俊聪, 金小刚. 最小二乘网格的模型修补[J]. 工程图学学报, 2009, (5): 13-21.

[10]Lotan K, Ayellet T. Mesh Segmentation Refinement Pacific [J]. Graphics, 2009, 28(7): 1995-2003.