湖南某预应力混凝土箱梁桥崩裂原因分析*
林小雄,钟新谷,舒小娟
(1.广西建设职业技术学院城市建设与交通工程系,广西南宁 530003;2.湖南科技大学土木工程学院,湖南湘潭 411021)
1 工程概况
湖南某桥位于省道S204线,主桥跨径为62 m+5×105 m+62 m预应力连续箱梁桥,单箱单室箱型截面,箱梁根部梁高6m,跨中梁高2.8 m,底板厚度支点处为0.8 m,跨中部位为0.28 m,下缘曲线方程为y=0.001 3x2,在墩顶和跨中各设置一道横隔板,厚度分别为1.2 m和0.4 m(图1)。该桥合龙顺序为先边跨后中跨进行合龙,在对称合龙次边跨6#~7#墩和10#~11#墩后,张拉预应力的过程中,发现底板混凝土大面积崩裂,施工单位立即停止施工。经查阅设计图纸可知,该桥的抗崩设计参数符合规范[1]的规定,但若考虑箱梁悬臂施工特点对等效径向力的影响,则防崩钢筋配置不足,抗崩设计参数存在一定问题。

图1 湖南某连箱梁桥Fig.1 Bridge in Hunan
2 等效径向力分析
精确计算等效径向力并与实际崩力相符合是防治崩裂的关键[2-10]。变截面预应力混凝土箱型桥一般采自平衡施工,合龙后后期索一般沿底板线形而布置,曲线预应力束张拉会产生沿曲心方向的等效径向力q(图2)。现行规范[1]提供了等效径向力计算公式q规范=1.2F/R(其中R为曲率半径;1.2为考虑其他因素的安全系数,预应力束按理论设计线形布索时规范[1]安全系数1.2可确保工程安全)。但大跨度预应力混凝土箱梁桥自平衡施工过程中采用分段直线,施工完成后箱梁底板是由多段折线组成,同时在施工过程中,波纹管定位与理论线形总是存在一定的偏差,定位误差是客观存在的,这些因素均会影响R的变化。因此,同时考虑施工过程的分段直线、施工定位误差预应力混凝土箱梁底板径向力影响后,现行规范[1]的安全系数1.2已无法确保工程安全,在抗崩参数设计时应合理考虑这一特点。
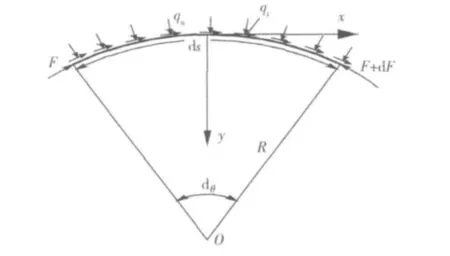
图2 等效径向力分析示意图Fig.2 Analysis of equivalent radial force
现分析定位误差对等效径向力的影响,设K1为定位误差影响系数,原预应力束抛物线方程为y=axn,每施工块的定位误差控制标准为Δ,Li为某施工梁段的起点在坐标,Li+1为某施工梁段的终点在坐标如图3所示,则变化后的曲率半径为:
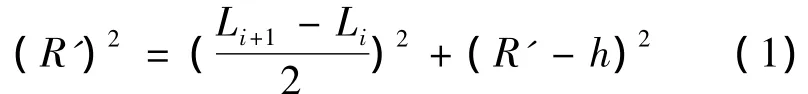
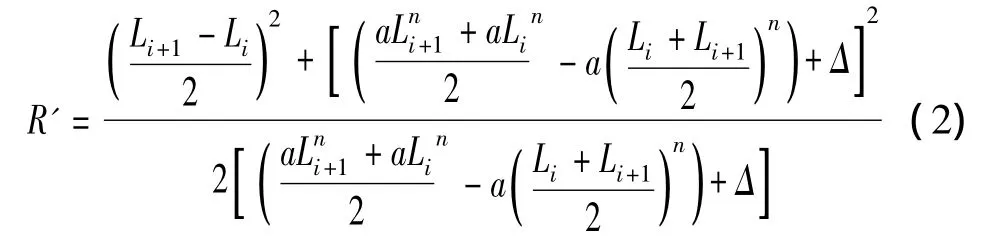
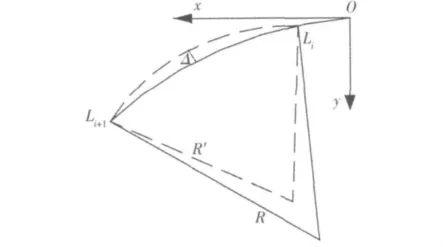
图3 定位误差分析图Fig.3 Analysis of positioning error
由式(1)解得:抛物线在施工梁段中点的曲率半径为R为:
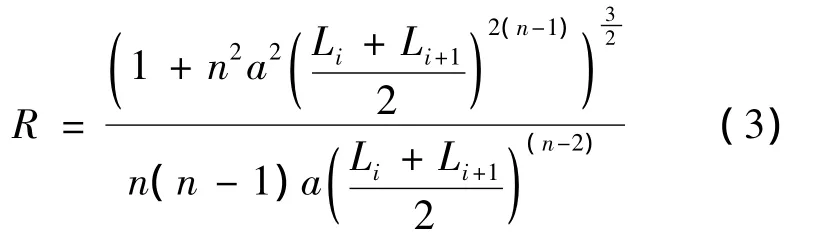
由式(2)和(3)有:
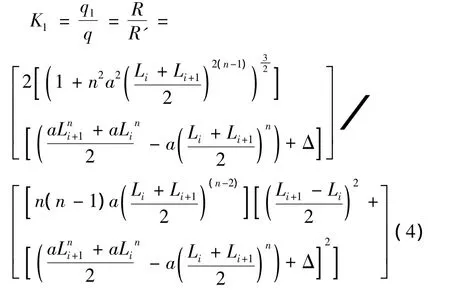
现分析折线拟和抛物线对等效径向力的影响,设K2为折线拟合抛物线影响系数,取一施工梁段来其长度为Δx,如图4所示。图4中:θ1和θ2相邻折线延长线的夹角;β为相邻折线延长线顶点夹角;α为折点上抛物线切线顶点夹角。将张拉力N0分解到平行于施工段L3和垂直于施工段L3折线上,得:
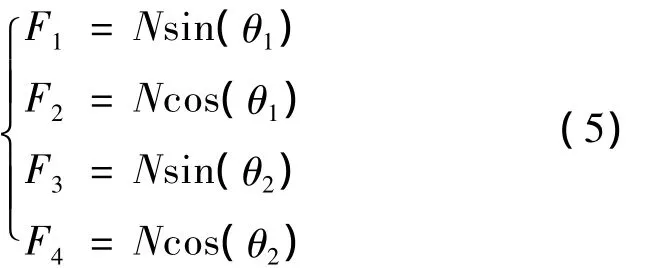
因此,可得q2:
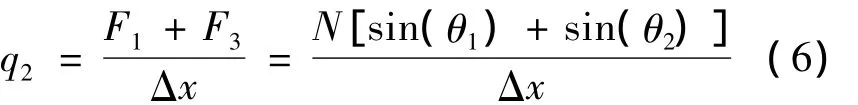
由于Δx相对于L很小,所以,可取sinθ1≈θ1,sinθ2≈ θ2,则式(6)可化简成:
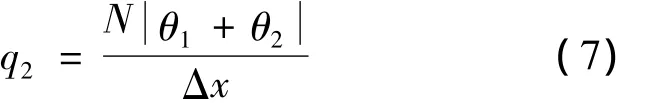
由于Δx很小,因此,β≈α,由三角形内角和定理得:
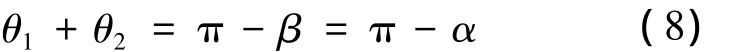
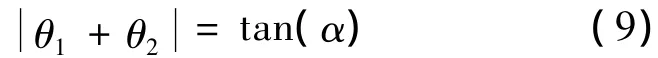
由于 θ1+ θ2很小,因此,设预应力束曲线方程为y=axn则有:
将式(10)代入式(7)得:
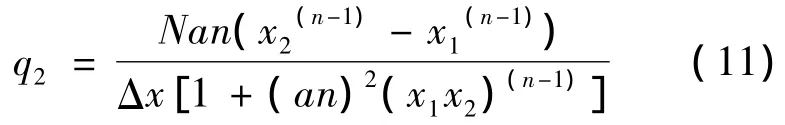
与抛物线等效径向力公式对比得:
综合上述分析,结合式(4)和(12),预应力混凝土箱梁桥底板预应力束按抛物线设置时,考虑定位误差和折线法施工影响后的等效径向力可按下式计算:

其中:综合影响系数K=K1K2。
表1列出了等效径向力根据规范[1]公式规范值与式(13)计算修正值。
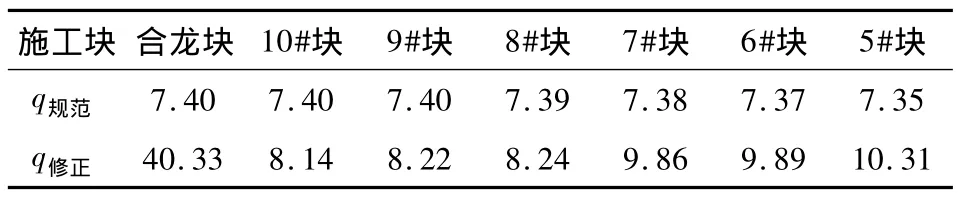
表1 湖南某桥q值Table 1 q of bridge in Hunan
湖南某预应力连续箱梁桥根据规范[1]公式均匀布置和修正公式(13)计算的防崩钢筋面积见表2。
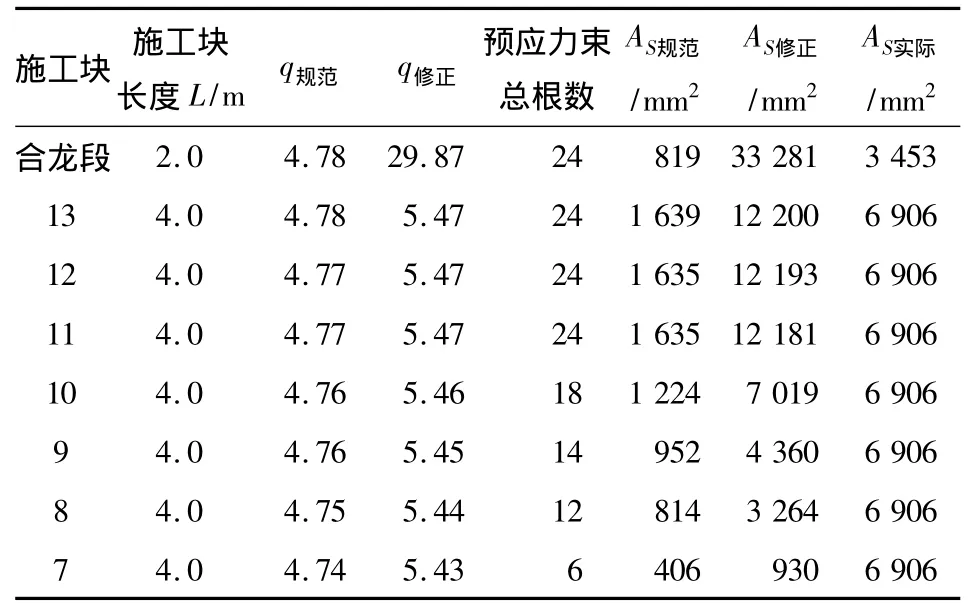
表2 湖南某桥ASTable 2 AS of bridge in Hunan
由表1可知:该桥实际配置的的防崩钢筋面积为规范公式所得的5倍左右,10#块至合龙段比修正公式所得结果低,该桥防崩钢筋满足规范[1]的要求;而底板束考虑箱梁桥悬臂施工特点对等效径向力影响后,防崩钢筋配置不足。这是该桥崩裂的主要原因。
3 有限元数值分析
3.1 全桥整体应力分析
湖南某桥底板崩裂主要发生在施工阶段,因此采用MIDAS有限元程序对该桥施工阶段进行分析。施工阶段荷载主要有结构的自重、预应力荷载及施工荷载,全桥合龙完成后的箱梁纵向应力见图5。由图5可知:该桥合龙阶段全截面受压,且在规范限值内,结构在施工阶段是安全可靠的。为了检验该桥成桥的受力状况,进行4种工况计算:①恒载+汽车;②恒载+满布人群;③恒载+汽车+温度;④恒载+汽车+强迫位移+温度,计算结果表明上部结构在最不利荷载作用下的最小应力为 -0.5 MPa,满足《规范》[1]的要求。因此,该桥施工阶段和使用阶段都是安全可靠的,出现崩裂主要是局部受力出现问题。

图5 湖南某桥底板张拉阶段的法向应力图Fig.5 Normal stress in bottom slab of a Hunan bridge on tension phase
3.2 次边跨崩裂实体单元分析
次边跨实体单元分析采用ANSYS有限元程序分析,由于截面和荷载的对称性,因此可以取1/4次边跨进行分析,次边跨合龙后结构在自重、预应力荷载的作用下的1/4模型的竖向应力见图6。

图6 1/4次边跨竖向应力云图(Pa)Fig.6 Vertical stress in 1/4 secondly span
由图6可知:竖向应力较大值主要出现在次边跨的合龙段及其附近梁段腹板倒角部位,竖向拉应力高达到2.78 MPa,局部达5.04 MPa。因此,底板竖向拉应力很大,当防崩钢筋配置不足时极易崩裂。
对底板不同区域的应力分布情况进行分析,其区域划分见图7。
图7 底板区域划分示意图Fig.7 Vertical stress in 1/4 secondly span
根据有限元计算结果取次边跨跨中合龙段竖向应力云图见图8。
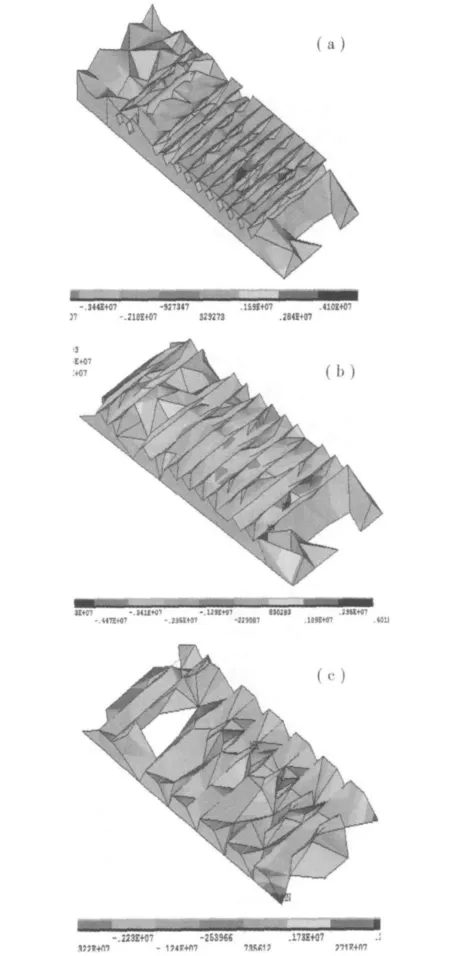
图8 底板合龙段竖向应力云图(Pa)Fig.8 Vertical stresses on slab bottom
由图8可知:底板上表面为拉应力,下表面基本为压应力,最危险的截面在1/2波纹管截面处。设为第i分块区域竖向拉应力平均值,si为分块区域横向宽度,Li为施工段长度,Ωi为第i分块区域小面积,则竖向拉力Pi为:

其中:Ωi=siLi,si孔肋取最薄的厚度;管道部位取1/2圆弧周长。
因此,有限元数值分析需配置的防崩钢筋面积为:

其中:fsd为防崩钢筋的抗拉强度。
现由图8及(15)式计算合龙段每分块区域的防崩钢筋面积并与本文提出的计算公式(13)式计算的防崩钢筋面积比较,其结果见表3。
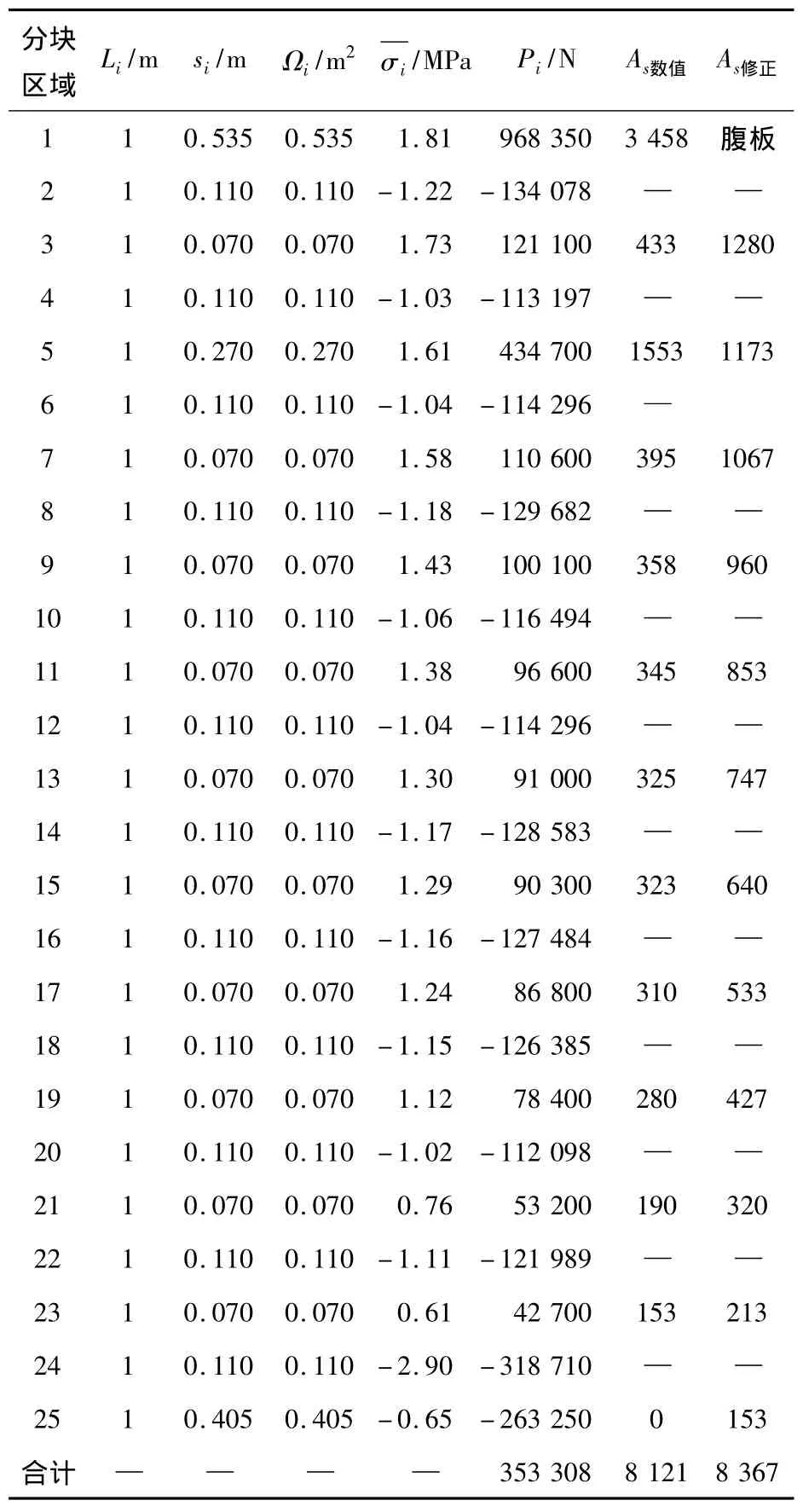
表3 1/4合龙段分块区域防崩钢筋配置表Table 3 Anti-collapse steel in 1/4 closure segment
由表3可知:波纹管下方混凝土受压,孔肋受拉,数值分析的竖向拉压力之和∑Pi=353.3 kN,而总的等效径向力∑qiLi=358.4 kN,两者基本相等。在等效径向力的作用,孔肋拉力在横向呈现不均匀分布,靠近腹板区域拉力大,反之则小,因此,防崩钢筋在横向应采取不均匀布置。由表3可知:分块区域数值分析与修正公式计算的防崩钢筋基本上 As修正> As数值,而∑As修正≈∑As数值,证明了本文提出的修正公式的合理性。因此,按本文提出的修正后的等效径向力作为崩力依据配置防崩钢筋是安全可靠的。
4 结论
(1)湖南某桥底板抗崩设计参数满足文献[1]中规范的规定,崩裂主要是由于等效径向力计算时未考虑箱梁桥悬臂施工特点造成的。
(2)箱梁桥即使满足整体应力要求,底板在等效径向力作用下也有可能崩裂,因此,箱梁底板应进行整体应力计算和局部应力计算。
(3)箱梁桥采用悬臂法施工时底板束偏离了理论线形导致了等效径向力的增大,按文献[1]中规范配置的防崩裂钢筋往往不足,因此,防崩钢筋设计时应合理考虑这一点。本文提出的修正公式符合实际应力分布规律,因此,修正后的崩力作为外力的依据可确保工程安全。
[1]JTG D62—2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].JTG D62—2004,Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].
[2]林小雄.预应力混凝土变截面箱梁桥底板抗崩设计参数研究[D].湘潭:湖南科技大学,2012.LIN Xiao-xiong.Research on design parameters of bursting crack in bottom slab of PC box-girder bridge(Master Degree Thesis)[D].Xiangtan:Hunan University of Science and Technology,2012.
[3]娄晟嘉,杨吉新.预应力混凝土连续刚构桥底板脱落成因分析[J].中外公路,2010(3):190-193.LOU Cheng-jia,YANG Ji-xin.Bottom slab of prestressed concrete continuous rigid frame bridge off analysis[j].Journal of China& Foreign Highway,2010(3):190-193.
[4]包立新,杨广来,杨文军.对连续刚构底板开裂问题的探讨[J].公路,2004(8):39-41.BAO Li-xing,YANG Guang-lai,YANG Wen-jun.Approach to crack problems of bottom plate of continuous rigid frame bridge[J].Highway,2004(8):39 -41.
[5]Roberts C L.Behavior and design of the local anchorage zone in post- tensioned concrete[D].Austin,TX:University of Texas,1990.
[6]Stone W C,Breen JE.Behavior of post-tensioned girder anchorage zones[J].PCI Journal,1984,29(1):64 -109.
[7]项贻强,唐国斌,朱汉华,等.预应力混凝土箱梁桥施工过程中底板崩裂破坏机理分析[J].中国公路学报,2010,23(5):70-75.XIANG Yi-qiang,TANG Guo-bin,ZHU Han-hua,et al.Prestressed concrete box girder bridge construction process backplane crack failure mechanism[J].China Journal of Highway and Transport,2010,20(5):70 -75.
[8]冯鹏程,吴游宇,杨耀铨,等.连续刚构桥底板崩裂事故的评析[J].世界桥梁,2006(1):66-69.FENG Peng-cheng,WU You-yu,YANG Yao-quan,et al.Analysis of accident of bursting crack in bottom slab of a continuous rigid - frame bridge[J].World Bridges,2006(1):66-69.
[9]潘钻峰,吕志涛.大跨径连续刚构桥主跨底板合龙预应力束的空间效应研究[J].世界桥梁,2006(4):36-39.PAN Zuan-feng,LV Zhi-tao.Study of spatial effect of closure prestressing strands in main span bottom slab of long span continuous rigid - frame bridge[J].World Bridges,2006(4):36-39.
[10]魏乐永,沈旭东,肖汝诚,等.预应力混凝土连续箱梁底板崩裂破坏的机理及其对策[J].结构工程师,2007,23(2):53 -57.WEI Le-yong,SHEN Xu-dong,XIAO Ru-cheng,et al.Cracking for bottom slab in a continuous prestressed concrete box girder[J].Structural Engineers,2007,23(2):53-57.

