考虑阻尼值修正的双链式悬索桥地震响应分析*

林丽霞，丁南宏，张元海，吴亚平

(兰州交通大学土木工程学院，甘肃兰州 730070)

双链式悬索桥指在1个吊杆平面内设有两条主缆的悬索桥，该2条主缆在跨中交叉且互相联结，上下主缆在全跨范围内均匀布置有吊索吊拉桥面加劲梁［1］，如图1所示。双链式悬索桥对恒载和全跨布置的均布活载是由其上下主缆平均负担。当半跨有活载时，荷载将由该半跨的下主缆全部承受，而下主缆此时的形状，恰好符合于承受荷载后主缆的变形，悬索桥将不发生S形变形，因而，它比单索体系有较大的刚度，其对非对称荷载的适应性较强。可以说，双链式悬索桥静力和变形特性的优点是显著的，但对该类悬索桥动力性能分析的报道非常少。双链式悬索桥的结构特性，决定了其具有独特的动力特性和抗震性能。本文作者曾就双链式悬索桥自振特性进行了研究，并与同跨度同矢高的单根主缆悬索桥进行了对比分析［2］。日前国内外有许多学者对大跨度悬索桥进行了地震响应的研究［3～6］，但研究对象几乎都为1个吊杆平面内设有1根主缆的悬索桥，而对于双链式悬索桥的抗震性能研究还是空白。为保证双链式悬索桥这种特殊结构形式的抗震安全性，探讨其抗震性能的特点和规律，寻求合理的抗震结构体系将有着十分重要的工程意义。

双链式悬索桥是钢材(加劲梁、主缆、吊索)和钢筋混凝土(主塔)两种阻尼特性不同的材料组合体，故不能采用单一阻尼参数来表达，需要考虑不同材料的阻尼耗能差异，这会导致主坐标系中的运动方程耦联。文献［7－8］采用复振型方法进行分析，取得了满意的结果，但由于复振型方法非常复杂，又没有相应的结构计算软件的配合，工程师很难用此方法进行实际结构分析。文献［9］采用强迫解耦的方法，利用经典阻尼理论对非经典阻尼结构进行分析，研究表明［10］:当结构阻尼比较小时，分析结果具有较好的误差控制，可以为设计采用。基于复阻尼理论求解换算阻尼系数和等效粘滞阻尼比，计算数据与试验数据符合程度较好［11］，说明该方法能够反映不同材料组成的结构的实际情况。

本文以某双链柔式钢索悬索桥为工程背景，针对双链式悬索桥独特的结构形式，采用等效粘滞阻尼比近似描述非经典阻尼体系的阻尼耗能，提出了考虑实测阻尼值修正的非经典阻尼双链式悬索桥地震响应分析方法。对比分析了按经典阻尼0.02和0.05及非经典阻尼对双链式悬索桥地震响应的影响。

1 非经典阻尼分析方法

1.1 等效黏滞阻尼比

设组成双链式悬索桥的两种材料钢材和混凝土的阻尼系数分别为γs和γc，刚度矩阵分别为［K］s和［K］c;结构质量矩阵为［M］，动力荷载为{P(t)}。根据Сорокин复阻尼理论，振动方程为:

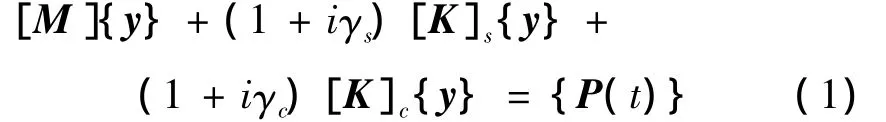
设{y}=［φ］{q}，［φ］为振型向量组成的矩阵，代入式(1)，并左乘第j振型的振型向量{φ}Tj，由振型正交性得到:

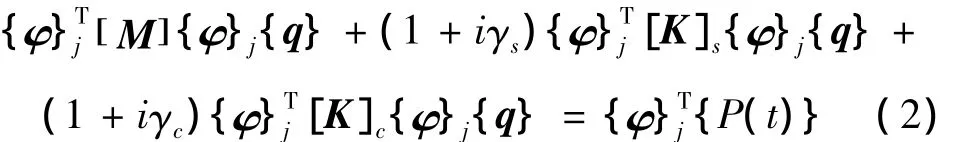
与结构换算阻尼系数为γ的振动方程比较，得到:

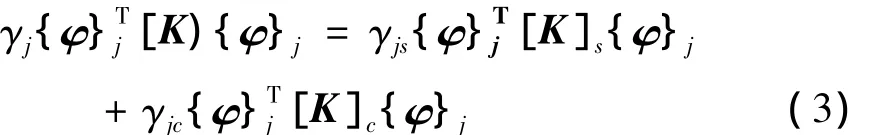
设振型中与钢构件相关的振型向量为{φ}js，与混凝土构件相关的振型向量为{φ}jc，由式(3)得到换算阻尼系数:

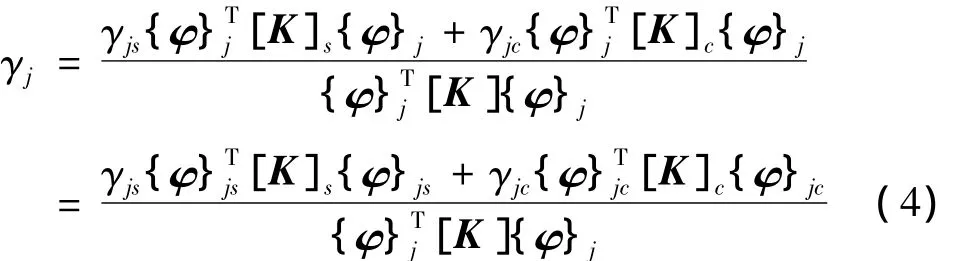
则等效黏滞阻尼比为:

1.2 考虑阻尼实测值的修正方法

阻尼直接关系到桥梁在动荷载作用下振动的强弱，因此，研究桥梁的阻尼规律是提高桥梁动力计算精度的关键之一。

Davenport等在研究了一些国外悬索桥模态阻尼实测资料后，提出了一些大跨索支承桥梁的阻尼分布特性［12］。文献［13］根据1座国内钢悬索桥(虎门桥)的实测阻尼资料，得到了相同的规律，模态阻尼ξ与固有频率f的关系可近似表示为:

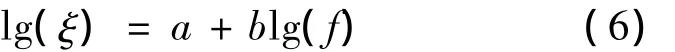
只要实测到两阶固有频率及相应模态阻尼值，则可确定系数a和b的取值，从而确定各阶模态阻尼值。双链式悬索桥一个显著的动力特性就是动力反应中会出现十分明显的振型分组现象［2］，即以加劲梁振动为主的振型最先出现，而后是索的振动和梁的高阶振型，以塔为主的振动出现较后。若测得以加劲梁(钢构件)振动为主的阻尼比ξs，以主塔(混凝土构件)振动为主的阻尼比ξc，结合振型分组的特点，可设加劲梁第一阶振型阻尼比为ξs，主塔第一阶振型阻尼比为ξc，然后利用上述非经典阻尼分析方法，可得到比较精确的地震响应。

2 双链式悬索桥反应谱法分析

2.1 双链悬索桥有限元模型

青城桥距黄河大峡水库下游3 km处，结构形式为单跨180 m的双链柔式钢索悬索桥，边跨为4×16 m简支梁，如图1所示。该悬索桥加劲梁为16 Mn工字钢纵横梁传力体系，具体结构参数见文献［2］。

建立空间有限元模型，考虑:(1)采用全桥脊梁模式，主缆和吊索采用只受拉三维杆单元［2］;主跨加劲梁采用空间梁单元和刚臂单元模拟;主塔采用空间梁单元;(2)对于主缆和吊索等柔性构件，计入轴向拉力对刚度的贡献，即用几何刚度矩阵考虑恒载索力的线性二阶影响;(3)边界条件为塔底在地面固结，锚碇与地基固结。

对于非线性效应突出的悬索结构，在动力分析之前须进行恒载起点的非线性静力分析，以计入恒载起点的P－Δ效应及几何非线性效应的影响。采用Newton－Raphson迭代求解，确定结构在自重下的切线刚度矩阵，然后在此基础上进行动力特性分析。双链式悬索桥具有普通悬索桥振型分组显著的特性［2］，单链悬索桥第一振型一般为反对称竖弯，而双链悬索桥第一振型为正对称竖弯，在相同结构参数情况下，双链悬索桥能有效提高桥梁一阶竖弯振动频率。

2.2 反应谱法

反应谱振型分解法的振型组合方式及应组合的振型数对大跨悬索桥地震反应的影响十分显著。依据文献［14－15］建议，本桥反应谱振型分解法使用CQC组合，组合振型时使用前200个振型。设青城桥的加劲梁、主缆和吊杆阻尼比ξs=0.02，混凝土主塔阻尼比ξc=0.05。该桥7度设防，II类场地土，根据《公路桥梁抗震设计细则》(JTG/T B02—01—2008)选定设计反应谱。纵向地震响应见表1。

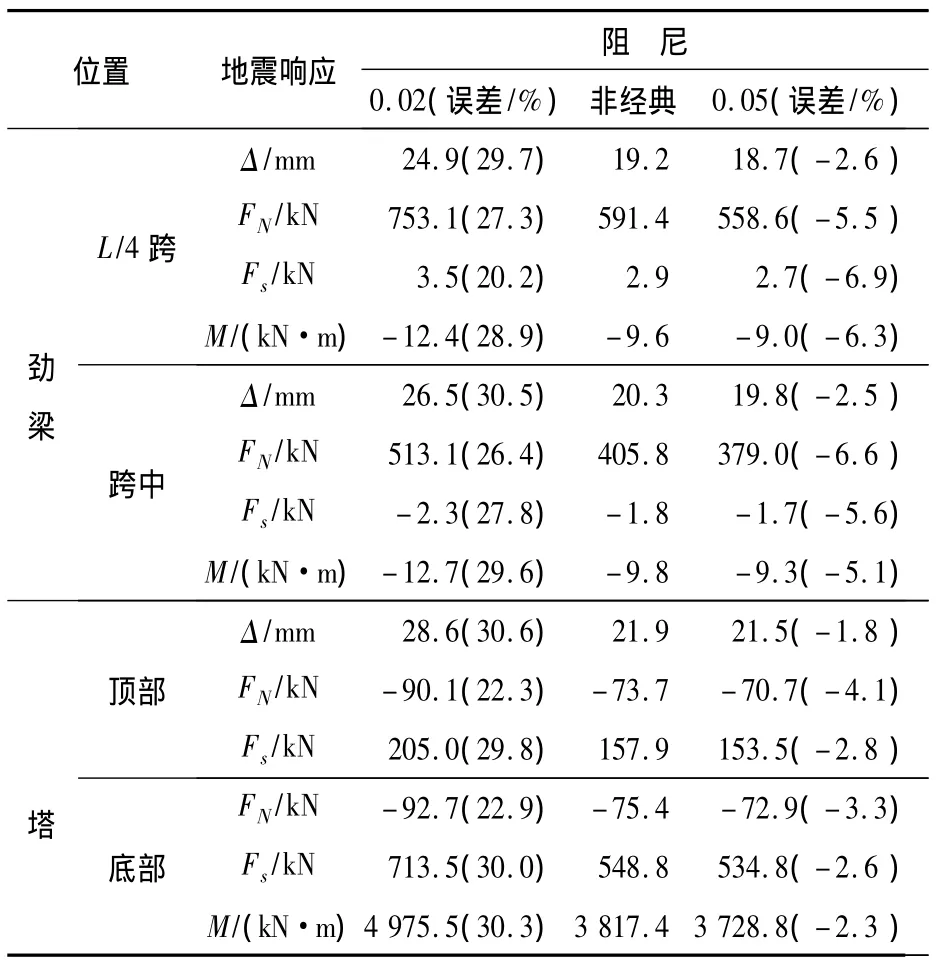
表1 纵向地震响应Table 1 Longitudinal seismic response

从表1可见:按非经典阻尼计算结果介于整个结构按混凝土和钢材阻尼计算结果之间，加劲梁非经典阻尼顺桥向位移Δ、轴力FN、面内剪力Fs、面内弯矩M及塔顶顺桥向位移Δ、顺桥向剪力Fs、面内弯矩M明显偏向按混凝土阻尼计算结果，但加劲梁内力偏差大于主塔内力的偏差。如按非经典阻尼计算的塔顶最大位移与按0.02阻尼比计算结果有30.6%的误差，与按0.05阻尼比计算结果比较接近，只有－1.8%的误差;但按非经典阻尼计算的加劲梁L/4跨轴力与按0.02阻尼比计算结果有20.2%的误差，与按0.05阻尼比计算结果有6.9%的误差。其原因是:纵向地震激励下，全桥以主塔顺桥向振动为主，因此与之相关的结构响应依赖于主塔振动形式。

另外，按非经典阻尼计算的主缆内力介于按混凝土和钢材阻尼计算结果之间，稍偏向于按混凝土阻尼计算结果。原因:主缆与索塔和吊索加劲梁连接，受二者共同影响，只是主塔影响更为明显。横向地震响应见表2。

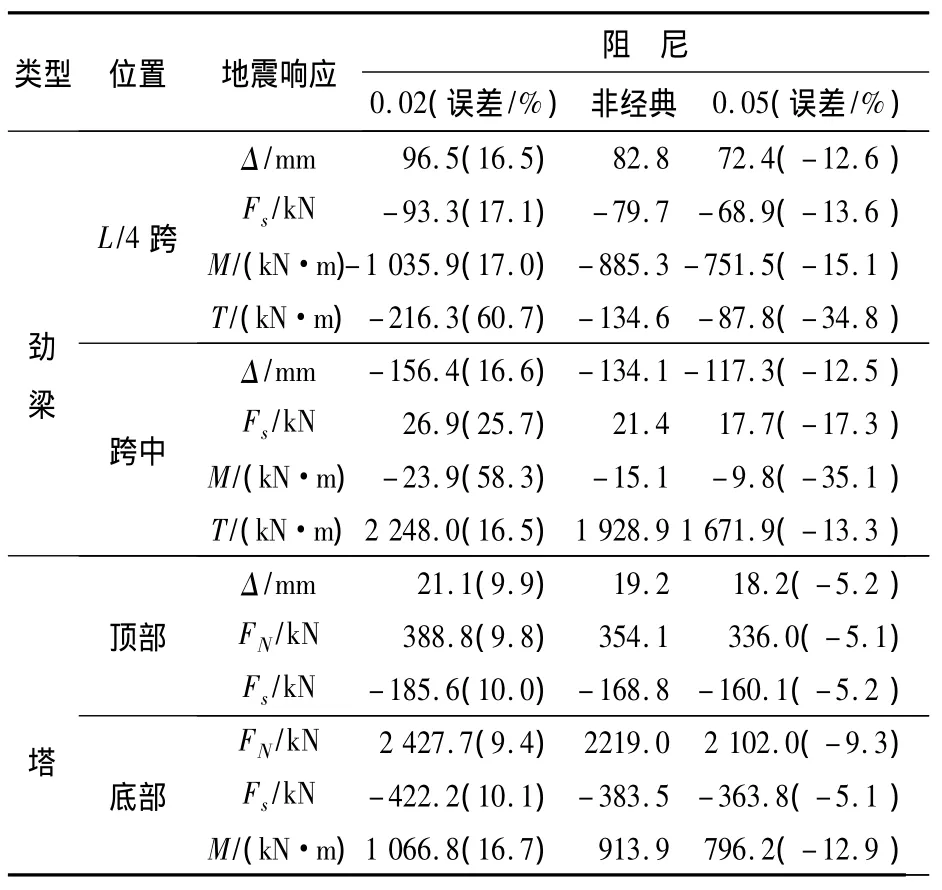
表2 横向地震响应Table 2 Transverse seismic response

从表2可见:按非经典阻尼计算结果介于整个结构按混凝土和钢材阻尼计算结果之间，按非经典阻尼计算的加劲梁横向位移Δ、横向剪力Fs、面外弯矩M和扭矩T稍偏向混凝土阻尼计算结果;另外，塔顶横向位移Δ、轴力FN、横向剪力Fs、面外弯矩M及主缆内力有同样规律。原因在于:双链式悬索桥主要组成部件主塔、主缆和加劲梁，在横向振动时，互相牵制。任一部件的振动可视为约束部件振动与本身构件振动的叠加，如加劲梁为钢构件，同时受到钢主缆、钢吊索和混凝土主塔的约束。竖向地震响应见表3。

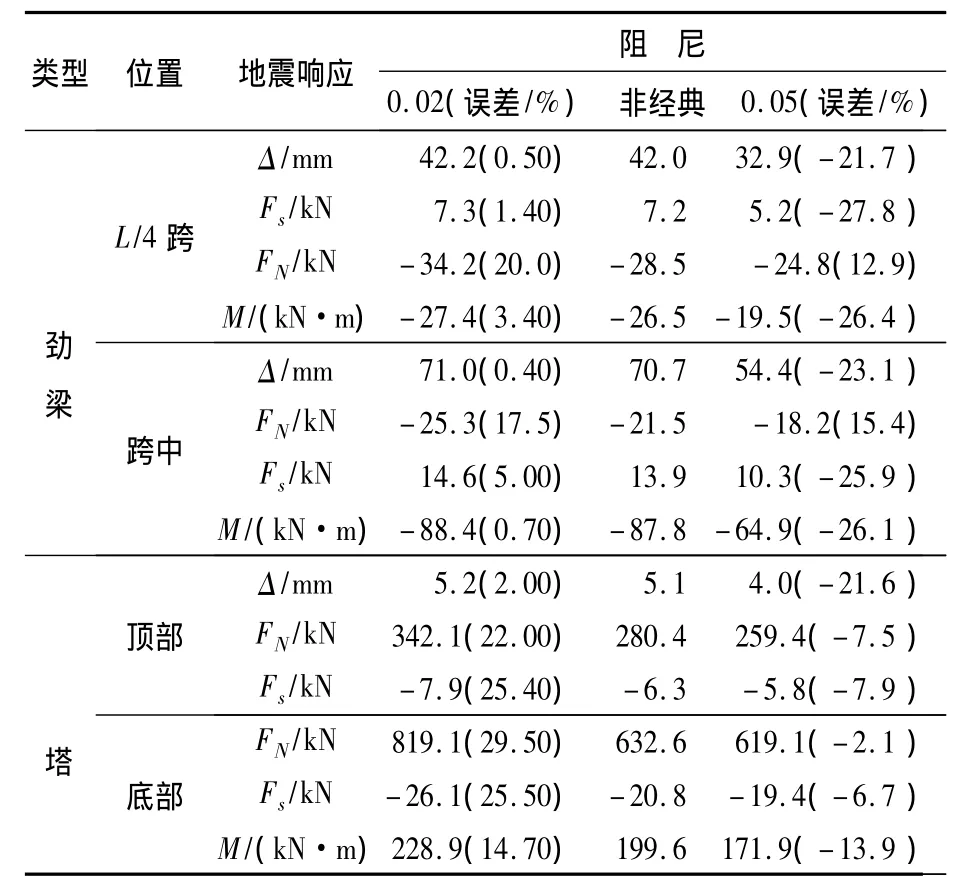
表3 竖向地震响应Table 3 Vertical seismic response

从表3可见:非经典阻尼计算结果介于整个结构按混凝土和钢材阻尼计算结果之间，加劲梁非经典阻尼竖向位移、竖向剪力、面内弯矩明显偏向钢材阻尼计算结果，原因在于:加劲梁竖向与吊索及主缆连接，受到其约束，而主塔竖向位移很小。另外，主缆内力有与加劲梁同样规律。而主塔竖向地震响应比较复杂，塔顶顺桥向位移偏向混凝土阻尼计算结果，顺桥向剪力明显偏向混凝土阻尼计算结果，面内弯矩稍偏向混凝土阻尼计算结果。

3 双链式悬索桥时程响应分析

有限元模型如前所述，时程分析采用时域内逐步积分的Wilson－θ法，计算步长取0.02 s。时程积分时的地震记录的持续时间对大跨悬索桥地震响应的影响十分显著。依据文献［15］建议:用时程积分法时，地震波的持续时间应尽可能长，一般可取60 s左右;竖向地震必须考虑，竖向地震加速度取相应的水平向加速度的2/3。据此，从历次强震记录中选取了EI－Centro波作为地震动输入。

加劲梁跨中位移时程曲线如图2和图3所示。横向位移各时点计算值基本上介于按混凝土和钢材阻尼计算结果之间，在t=6.8 s时，得到最大值。相应于经典阻尼0.02、非经典阻尼和经典阻尼0.05，最大值分别为0.441，0.409 和 0.373 m;以非经典阻尼计算结果为准，按经典阻尼0.02和0.05计算结果偏差分别为8.0%和－8.7%。

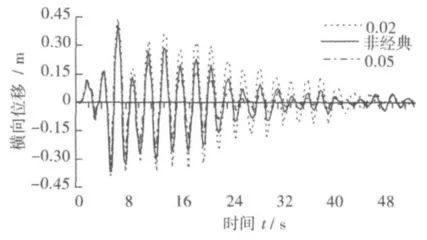
图2 加劲梁跨中横向位移时程曲线Fig.2 Transverse displacement time histories on middle span of stiffening girder

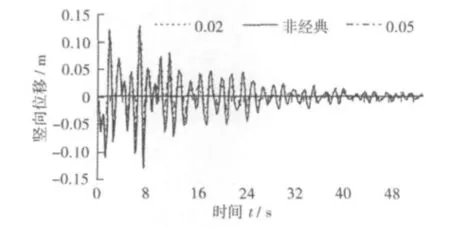
图3 加劲梁跨中竖向位移时程曲线Fig.3 Vertical displacement time histories on middle span of stiffening girder

按非经典阻尼计算所得各时点竖向位移值明显偏向于钢材阻尼计算结果，在t=7.0 s时，得到最大值。相应于经典阻尼0.02、非经典阻尼和经典阻尼0.05，最 大 值 分 别 为 0.130，0.129 和0.081 m;以非经典阻尼计算结果为准，按经典阻尼0.02和 0.05计算结果偏差分别为 0.6% 和－36.7%。

考虑横向地震波输入，主塔面外弯矩包络图如图4所示。以非经典阻尼计算结果为准，按经典阻尼0.02和0.05计算结果最大偏差分别为10.1%和 －11.3%。

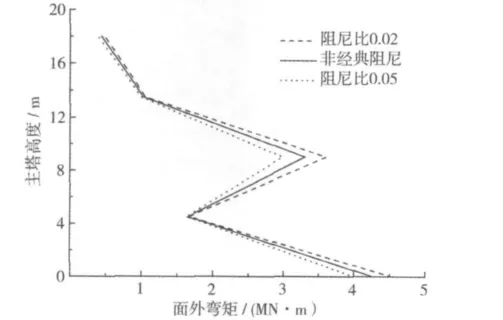
图4 主塔面外弯矩包络图Fig.4 Out－of－plane moment envelope diagram of main tower

4 结论

(1)考虑实测阻尼值修正，采用等效粘滞阻尼比反映双链式悬索桥非经典阻尼耗能特性，可得到较真实的地震响应。

(2)双链式悬索桥具有明显的非经典阻尼性质，其地震响应无论采用0.02的经典阻尼(钢结构阻尼)模型还是0.05的经典阻尼(混凝土结构阻尼)模型均会带来显著误差。故对双链式悬索桥的地震响应分析，应当使用非经典阻尼模型。

(3)在对具有非经典阻尼特性的双链式悬索桥进行地震响应的初步分析时，在纵向地震激励下，可用全桥按混凝土桥塔阻尼比计算所得地震响应代替非经典阻尼体系的地震响应;在竖向地震激励下，可用全桥按钢加劲梁阻尼比计算所得地震响应代替非经典阻尼体系加劲梁的地震响应。上述方法一般不会引起显著误差，但在横向地震激励下，非经典阻尼对结构地震响应影响明显，必须按非经典阻尼模型分析。

［1］雷俊卿.悬索桥设计［M］.北京:人民交通出版社.2001.LEI Jun-qing.Suspension bridge design［M］.Beijing:China Communication Press，2001.

［2］林丽霞，吴亚平，丁南宏.双索悬索桥结构参数对自振特性的影响分析［J］.铁道学报，2007，29(4):91 －95.LIN Li-xia，WU Ya-ping，DING Nan－ hong.Influence of structure parameters on natural vibration characteristics of double － cable suspension bridge［J］.Journal of the China Railway Society，2007，29(4):91 －95.

［3］Huang M H，Thambiratnam D P，Perera N J.Vibration characteristics of shallow suspension bridge with pre－tensioned cables［J］.Engineering Structures，2005，27(13):1220－1233.

［4］李志岭，秦 权.用RITZ法分析江阴悬索桥地震反应的影响［J］.工程力学，2003，20(1):32－36.LI Zhi-ling，QIN Quan.RITZ method for seismic response analysis of Jiangyin suspended bridge with non－classical damping［J］.Engineering Mechanics，2003，20(1):32 －36.

［5］ Arzoumanidis S，Shama Y，Ostadan A.Performance －based seismic analysis and design of suspension bridges［J］.Earthquake Engng Struct Dyn，2005，34(1):349 －317.

［6］秦 权，楼 磊.非经典阻尼对悬索桥地震反应的影响［J］.土木工程学报，1999，32(3):18 －22.QIN Quan，LOU Lei.Influences of non － classic damping on seismic responses of suspension bridges［J］.China Civil Engineering Journal，1997，32(3):17 －22.

［7］王建有，陈健云.基于复模态的非比例阻尼结构参数识别研究［J］.哈尔滨工业大学学报，2005，37(12):1647－1649.WANG Jian-you，CHEN Jian-yun.Study on parameters identification of non－proportional damping based on complex modes［J］.Journal of Harbin Institute of Technology，2005，37(12):1647 －1649.

［8］周锡元，董 娣，苏幼坡.非正交阻尼线性振动系统的复振型地震响应叠加分析方法［J］.土木工程学报，2003，36(5):31－36.ZHOU Xi-yuan，DONG Di，SU You-po.New method for linear systems with non－classical damping under ground motion［J］.China Civil Engineering Journal，2003，36(5):31－36.

［9］俞瑞芳，周锡元.非比例阻尼弹性结构地震反应强迫解耦方法的背景和数值检验［J］.工业建筑，2005，35(2):52－56.YU Rui-fang，ZHOU Xi-yuan.Theoretical and numerical research on forced uncoupling method for seismic response of non－classically damped linear system［J］.Industrial Construction，2005，35(2):52 －56.

［10］桂国庆，何玉敖.非比例阻尼结构体系近似解耦分析中的误差分析［J］.工程力学，1994(4):40－50.GUI Guo-qing，HE Yu-ao.Study on errors of approximated decoupling analysis for non－proportionally damped structural systems［J］.Engineering Mechanics，1994(4):40－50.

［11］龚炳年，郝锐坤，赵 宁.钢－混凝土混合结构模型动力特性的试验研究［J］，建筑结构学报，1995，16(3):37－43.GONG Bing-nian，HAO Rui-kun，ZHAO Ning.Experimental investigations of the dynamic characteristics of a 23 － storey steel－ RCmixed structure model［J］.Journal of Building Structures，1995，16(3):37 －43.

［12］Davenport A G，Larose G.The structural damping of long span bridges:an interpretation of observations［C］//Proc.of canada－japan workshop on bridge aerodynamics.Ottawa Canada，September 1989，111 －118.

［13］郭震山，陈艾荣，项海帆.大跨缆索承重桥梁的结构阻尼特性［J］.世界地震工程，2000，16(3):52 －57.GUO Zhen-shan， CHEN Ai-rong， XIANG Hai-fan.Charaeteristics of struetural damping of cable－supported bridges with long spans［J］.World Information on Earthquake Engineering，2000，16(3):52 －57.

［14］邓育林，贾贤盛.大跨度悬索桥地震反应中高阶振型的影响分析［J］.工程抗震与加固改造，2008，30(2):24 －24，81.DENG Yu-lin，JIA Xian-sheng.Effect of higher frequency models of vibration on seismic response of long－span suspension bridge［J］.Earthquake Resistant Engineering and Retrofitting，2008，30(2):24 －24，81.

［15］秦 权，罗 颖，孙 浩.悬索桥上部结构的抗震设计［J］.清华大学学报:自然科学版，1998，38(12):52－56.QIN Quan，LUOYing，SUN Hao.Seismic design of suspension bridge superstructures［J］.Journal of Tsinghua University:Sci＆ Tech，1998，38(12):52 －56.