权重线性组合与逻辑回归模型在滑坡易发性区划中的应用与比较

王进，郭靖，王卫东，方理刚

(中南大学 土木工程学院，湖南 长沙，410075)

滑坡是我国范围内发生最多、分布最广的地质灾害。根据国土资源部发布的数据，2010年全国共发生地质灾害30 670起，导致2 246人死亡，669人失踪，534人受伤，直接经济损失约 63.9亿元，其中滑坡22 329起，占地质灾害总数的72.8%[1]。可见：滑坡对人民的生命和财产安全构成严重的威胁，直接影响人口、资源和环境的协调发展。为合理开发和利用土地资源，有计划地开展地质灾害防治工作，对某一地区的滑坡进行调查、分析、评价和预测，编制滑坡易发性区划图并用于城市基础设施的初期规划，是应对地质灾害防患于未然的首选措施。在过去几十年中，经验模型、信息模型、统计预测模型、模式识别模型(专家系统、神经网络法)等在滑坡灾害评估研究中得到了广泛应用[2]。王卫东等[3-4]将数量化理论与地理信息系统紧密结合，采用半定量和定量2种方法分析滑坡的发生和各影响因素的关系，对区域滑坡易发性进行了空间预测和等级划分。吴益平等[5]将信息量模型、信息-物元模型、信息-神经网络模型用于滑坡易发性预测，通过对比3种模型的预测结果来分析每种模型的优劣，但尚未对模型的预测结果进行定量分析。在此，本文作者结合贵州省的滑坡发育特征，选取坡度、岩性和年均降雨量等10项评价指标，采用权重线性组合(WLC)模型及结合确定性系数的逻辑回归(LR)模型对研究区内滑坡易发性的空间分布进行预测和分区；通过与实际滑坡分布进行对比，运用熵值法对这2个模型的分区结果进行定量分析。

1 研究区概况与滑坡致灾因子

1.1 研究区概况

贵州位于我国西南部，国土面积176 128 km2，地处云贵高原向东部丘陵平原的过渡地带，地势由西向东逐渐降低；同时，又处于长江水系与珠江水系的分水岭，中部高，南北低，形成南北两面斜坡。省内地形起伏较大，平均海拔1 100 m左右。境内河网密布，岩溶分布广泛。多年降水量平均值为850～1 600 mm。贵州地层发育较全，自中元古界至第四系均有分布，层序大多连续，主要由沉积岩组成，又以碳酸盐岩地层最为发育，次为火山岩及火山碎屑岩。在山间河谷、盆地及丘陵地带，常有红黏土、软土等软弱堆积层。各种褶皱和断裂构造发育。综上所述，省内山高坡陡、降雨频繁，地质环境十分脆弱，是我国滑坡灾害最严重的省份之一。研究区内主要历史滑坡分布如图1所示。数据来源于贵州省国土部门1999-2004年的实地调查。根据现有资料统计，省内目前共有历史滑坡灾害点4 558处，占全省地质灾害总数的75.65%，其规模以中、小型为主。

图1 贵州省历史滑坡分布图Fig.1 Landslide inventory map of Guizhou Province

1.2 滑坡致灾因子

滑坡致灾因子一般可分为外在因子和内在因子[6]。内在因子如岩土类型、地质构造、地形地貌和水文地质情况等起控制作用。外在因子如地表水和地下水的作用、地震及人类工程活动(矿山开采和修建公路、铁路等)起触发作用。

根据贵州省滑坡发育特征，选取高程、坡度、坡向、地形地貌、岩性、至构造线距离、至铁路距离、至公路距离、至河流距离及年均降雨量10个因子作为致灾因子。各致灾因子及其分级如表1所示。

2 滑坡易发性空间预测模型

目前，滑坡易发性分析的建模方法可分为定性(或半定性)方法和定量方法[7-8]。定性方法以模糊方法为主，依赖专家的经验进行决策，具有一定的主观性。定量方法包括统计方法和确定性方法。统计方法基于历史滑坡资料，通过对影响滑坡的多个因子进行统计分析，寻找致灾因子和滑坡发生的量化关系。确定性方法则基于滑坡过程，通过力学定律计算沿滑面的局部平衡来确定边坡的稳定性，且此方法多用于单体滑坡评价。本文以主客观权重线性组合模型和结合确定性系数的逻辑回归模型为例，分别阐述其在区域滑坡易发性空间预测中的应用。其中，主客观权重线性组合模型是一种半定量方法，而逻辑回归模型是一种统计定量方法。

2.1 主客观权重线性组合模型

2.1.1 基于信息熵的一级因子客观权重

本文应用信息熵理论度量一级因子的致灾权重基于以下思想：若在某个因子的各二级因子对应的区域内，滑坡发生率(历史滑坡面积与区域总面积之比)无明显变化，则认为该因子对滑坡发生概率的影响不显著，应赋予该因子较小的权重；反之则应赋予较大的权重。

按下式计算滑坡发生率(面积密度)：

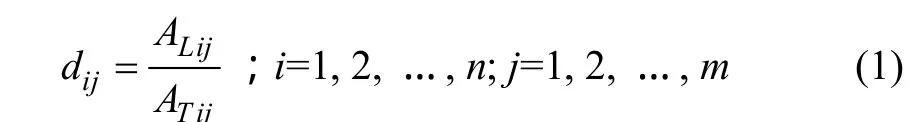
式中：ALij为第i个一级因子中第j个二级因子内的滑坡面积；ATij为第i个一级因子中第j个二级因子的区域总面积；dij为第i个一级因子中第j个二级因子的滑坡发生率；n为一级因子总数；m为二级因子总数。按下式计算滑坡发生率的归一化值Iij：

根据信息熵理论，按下式计算熵Hi：

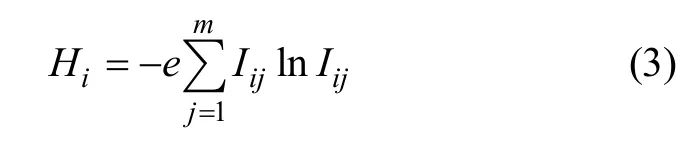
式中：e=1/lnm为常数，以保证0 ≤ Hi≤ 1。并规定：若 Iij= 0，则ln Iij= 0。

按下式计算每个一级因子的客观权重ωi：

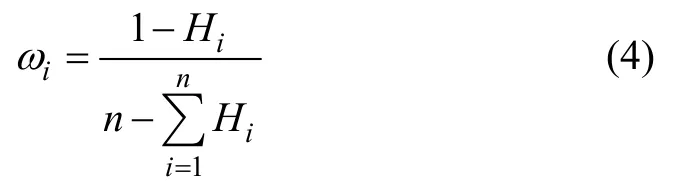
2.1.2 基于梯形模糊数的二级因子主观权重

该方法将自然语言评价信息转化为梯形模糊数，并通过对梯形模糊数进行聚合及无量纲化处理等步骤，实现对二级因子的赋权[9]。本文以 5个等级的自然语言和梯形模糊数评价各二级因子的相对重要性，即：很低(0, 0, 0, 3)，低(0, 3, 3, 5)，中等(3, 5, 5, 7)，高(5, 7, 7, 10)，很高(7, 10, 10, 10)。梯形模糊数定权法的步骤如下。

表1 滑坡致灾因子Table 1 Landslide causal factors

(2) 决策组成员应用上述的模糊评价词汇(很低，低，中等，高，很高)对各二级因子的相对重要性进行评价。设 w′jt= (ajt, bjt, cjt,djt)为第t个专家对某个一级因子中的第j个二级因子的模糊评价的量化值，则专家决策组对该二级因子的综合评价的量化值w′j表示如下：

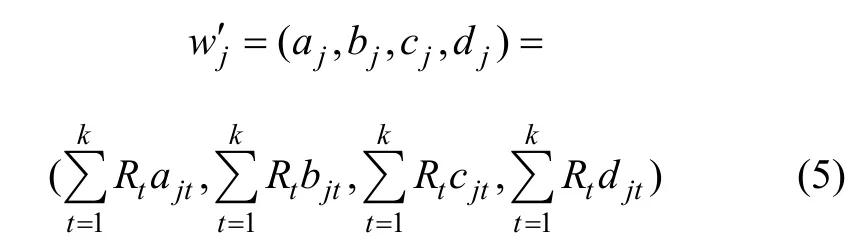
(3) 令 d( w ′j) = (aj+ bj+ cj+ dj)/4，按下式计算该二级因子的权重：

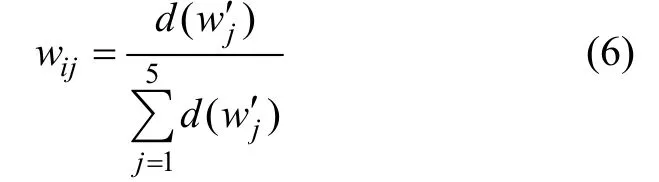
2.1.3 权重线性组合模型

滑坡是多个致灾因子共同作用的结果。权重线性组合模型的基本原理是：赋予每个一级因子一级致灾权重。同时，将每个一级因子划分为若干二级因子，赋予各二级因子二级致灾权重。将研究区网格化，划分为若干小单元，将各致灾因子图层叠加，每个单元对应的一、二级因子权重的线性组合即视为滑坡易发性的量化表达，称为不稳定分值[10-11]。

按下式计算不稳定分值：

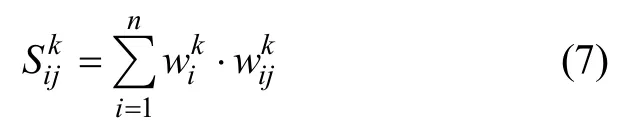
基于ArcMap软件平台对数据进行处理和分析。首先，通过图层叠加法统计各致灾因子区域内的滑坡发生率；其次，应用信息熵法确定致灾因子的一级客观权重，在这个过程中，剔除坡向、坡度和地形地貌3个权重最小的因子；然后，应用梯形模糊数定权法确定二级因子的主观权重；最后，应用 WLC模型计算各单元的不稳定分值。各级因子权重及不稳定分值计算结果如表2所示。

2.2 结合确定性系数的逻辑回归模型

2.2.1 基于确定性系数模型的滑坡关键因子的选取

确定性系数(Certainty Factor)模型的表达为1个概率函数[12]，表达式如下：

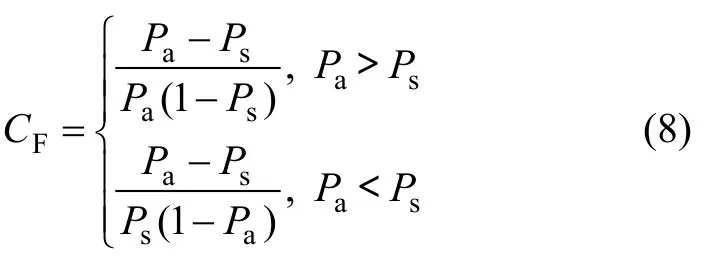
式中：Pa为单元a中事件发生的条件概率，以二级因子区域内滑坡面积与区域面积的比值表示；Ps为研究区内事件发生的先验概率，以研究区内滑坡面积与研究区总面积的比值表示；CF为二级因子确定性系数，CF∈[-1, 1]，其为正时，值越大，表明因子对滑坡发生的影响越显著(特殊地，Pa=1时，CF=1)；其为负时，值越小，表明因子对滑坡发生的影响越不显著(特殊地，Pa=0时，CF=-1)；CF接近于0，则不能确定因子与滑坡发生的关系。

按下式将一级因子集内各二级因子的确定性系数值依次进行合并，得到一级因子的确定性系数Z[13]：

式中：CF1和CF2为待合并的2个二级因子的确定性系数。本文拟定从一级因子集内最小的确定性系数开始，依次进行合并，得到一级因子的确定性系数 Z。Z越大，表明该一级因子对滑坡发生的影响越显著，据此选取滑坡发生的关键因子。经计算，高程、年均降雨量和坡向的确定性系数Z为负值，故认为这3个因子对滑坡发生的影响不显著，可以忽略。

2.2.2 逻辑回归模型

在滑坡易发性分析中，逻辑回归模型的作用就是寻找最优的拟合函数来描述滑坡发生与否(0代表不发生，1代表发生)和一组独立的参数如坡度、坡向、岩性等之间的关系[14-15]，基于此关系进而预测研究区内滑坡发生的概率。逻辑回归方程为：

式中：P为滑坡发生的概率，P∈[0, 1]；X为一组独立的因子变量，X=(1, x1, x2, …, xn)；而B为这组变量相应的系数，B=(b0, b1, b2, …, bn)。

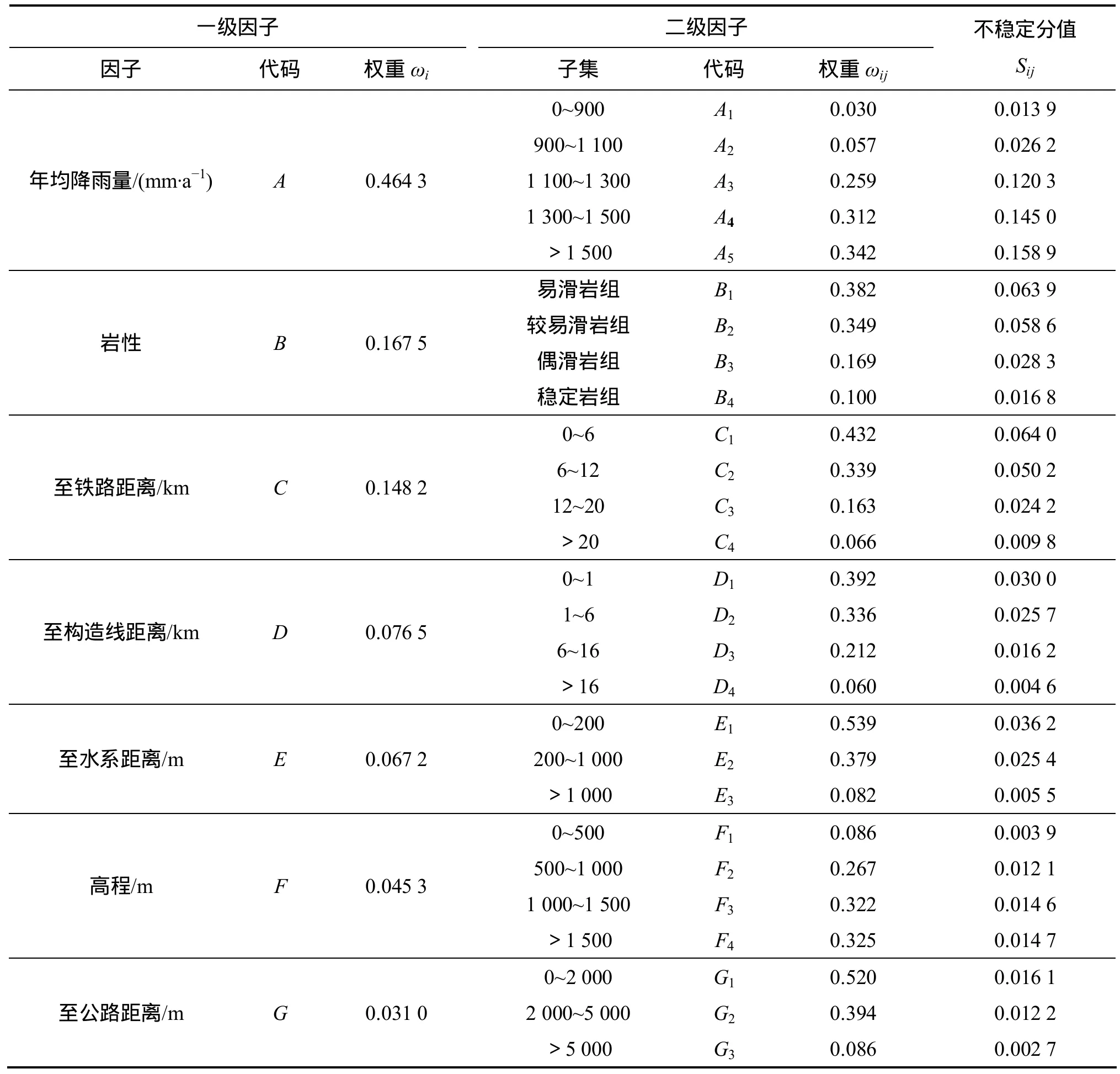
表2 因子权重Table 2 Susceptibility indices and weights of factors and their subclasses

为了使因变量的取值区间扩大到 (-∞, +∞ )，进行如下变换：

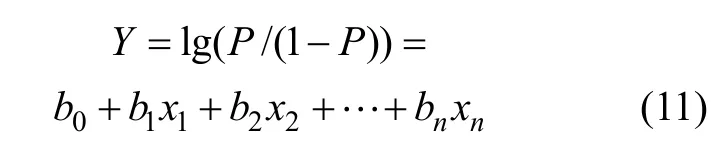
由于各因子变量的量纲和取值范围不同，为便于分析计算，把各因子统一到同一量纲，以滑坡面积密度归一化值 Iij(式(2))作为自变量，以灾害发生与否作为因变量进行分析。应用逻辑回归模型的步骤如下。

(1) 提取滑坡组和非滑坡组样本。在ArcMap中将研究区网格化，生成1 km×1 km的格网。将全部因子图层与历史滑坡图层叠加，每个格网单元中均包含了各因子的单一等级属性。提取全部的滑坡组单元，同时随机抽取等量的非滑坡组单元作为样本数据。

(2) 应用统计软件SPSS 17.0进行Logistic回归分析[16]。通过代入准备好的滑坡组和非滑坡组样本数据，拟合得到Logistic回归方程为：

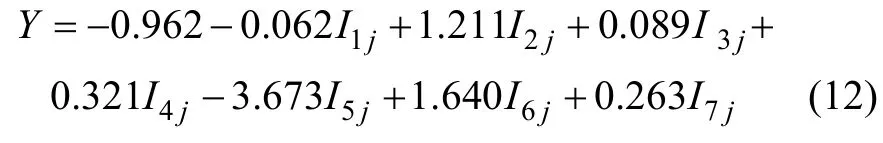
式中：I1j, I2j, …, I7j为自变量，依次表示格网单元内公路、河流、构造线、铁路、坡度、岩性和地形地貌因子的滑坡面积密度归一化值。根据 SPSS分析得到的结果，模型的似然比检验统计量2χ 为6 010.809，显著性检验统计量 Sig接近于0，小于所设的显著水平α=0.05，说明有显著性差异，模型通过检验。

(3) 依次应用式(12)和(11)计算每个格网单元的滑坡发生概率P。

3 滑坡易发性区划图及结果检验

通过应用WLC和LR模型对贵州省进行滑坡易发性的分析和预测，得到数值化的滑坡易发性分布图。根据WLC模型中不稳定分值Sij和LR模型中滑坡发生概率 P的分布，采用 ArcMap提供的自然断点法(Natural breaks)对贵州省滑坡易发性进行分级。这种分类方法的原则是将相似性最大的数据分在同一组，使得组间差异最大化。区划结果如图2所示。

由图2可见：尽管2张滑坡易发性区划图的分区存在一定差异，但主要的极易发区和易发区都集中在贵州西部的大方、水城、盘县、六枝特区，黔北的赤水、习水、桐梓、遵义，黔东北的石阡、思南、印江，黔东南的都匀、丹寨、荔波，黔西南的晴隆、贞丰、册亨以及黔中的息烽、修文、清镇一带；偶发区和少发区主要分布于贵州西部的威宁，黔北的正安、绥阳、务川、风冈、湄潭及黔西南的惠水、长顺、罗甸一带，其他地区有少量分布。

通过与实际的滑坡分布进行对比和统计来检验滑坡易发性区划图的分区效果。图3所示为这2种模型的分区结果中各易发区的滑坡面积和区域面积的分布比例。

图2 WLC模型和LR模型下的滑坡易发性区划图Fig.2 Susceptibility maps derived from WLC model and LR model

图3 WLC模型和LR模型各易发级别滑坡和区域面积分布比例Fig.3 Percentages of domain area and landslide area in each susceptibility zone obtained by WLC model and LR model

从图3可见：WLC模型的分区结果中，4个分区的面积近似相等，都约占贵州省国土面积的25%，但位于各分区内滑坡面积的比例则明显上升；分布在少发区、偶发区、易发区和极易发区内的滑坡面积分别占研究区滑坡总面积的 12.0%，21.8%，25.6%和40.6%。类似地，在LR模型的分区结果中，少发区占贵州省国土面积的 24.2%，但区内滑坡面积仅占研究区滑坡总面积的 5%；相反，极易发区占贵州省国土面积的17.2%，但区内滑坡面积的比例则高达38%。在此基础上，进一步计算了各区内滑坡的发生率，结果如图4所示。

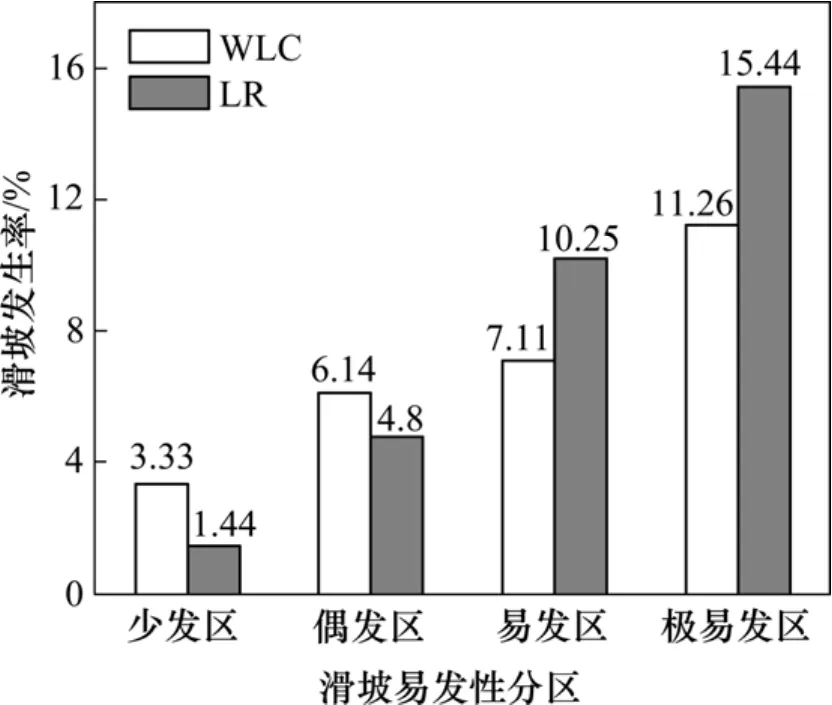
图4 WLC和LR模型结果中各分区内的滑坡发生率Fig.4 Landslide occurrence frequency in each susceptibility zone obtained by WLC and LR model

从图4可以看出：在这2种模型的分区结果中，历史滑坡的发生率都随着滑坡易发级别的递增而显著提高。这表明2个模型的易发性分区效果良好，都具有实践意义。采用熵权法(式(4))进一步定量地比较 2个模型结果的优劣。熵权是各组间滑坡发生率差异的度量，熵权越大，说明各组间滑坡发生率的差异越显著，表明区划的结果与实际滑坡的分布更加吻合。经计算，WLC模型分区结果的熵权为0.255，LR模型分区结果的熵权为0.745。这表明依据LR模型编制的滑坡易发性区划图的结果更优。究其原因，主观赋权方法往往只看到单个致灾因子的作用，很难表达各致灾因子间的相互作用和影响。若专家仅从一般经验出发而没有充分了解研究区内滑坡发育的实际情况，则很难估计因子的准确权重。

4 模型比较和讨论

权重线性组合模型属于半定量方法，首先分别获得影响因子的一、二级权重，然后通过进行线性运算得到综合权重。本文中，一级权重的赋权方法为信息熵法，二级权重的赋权方法为梯形模糊数法。通过将主观经验与客观权重结合，降低了决策者的主观评判带来的风险。这种方法简单易行，适用于历史资料不足的地区。其缺点是要求专家不但要有丰富的经验，而且应熟悉研究区滑坡发育的特点。

逻辑回归模型是一种统计学模型，其作用是将几个自变量间的关系描述为1个二分类因变量。逻辑回归模型的优势在于自变量可以是连续的，也可以是离散的，且不必满足正态分布。逻辑回归模型因为充分依赖历史数据，所以，其聚类结果具有较强的客观性和稳定性；其缺点是只适用于有丰富历史资料的地区。

此外，对于实现过程，权重线性组合模型的原理和应用都较简单，在基于地理信息系统时，其实现过程不需要依赖特别的统计软件。在得到各级因子的权重后，通过对图层进行加权叠加等操作即可实现应用。而逻辑回归模型则由于其计算过程较繁杂，需要统计分析软件(如 SPSS等)和地理信息系统的共同辅助和支持。

5 结论

(1) 以贵州省为研究区，选取坡度、岩性和年均降雨量等10项评价指标，采用半定量方法的主客观权重线性组合模型和定量方法的逻辑回归模型，基于ArcGIS平台进行区域滑坡易发性的分析和预测，编制了贵州省滑坡灾害易发性区划图。

(2) 结合实际滑坡对区划图的有效性进行验证。在这2个模型的分区结果中，历史滑坡灾害的发生率都随着滑坡易发级别的递增而显著提高，表明滑坡灾害易发性区划图和实际的滑坡分布基本一致，分区效果良好。

(3) WLC和LR模型分区结果的熵权分别为0.255和0.745，说明在该研究实例中，依据LR模型编制的滑坡易发性区划图的结果更优。

(4) 这 2种模型的原理和特点不同。在滑坡易发性的分析和预测中，应结合研究区实际情况合理选择区划模型。

[1] 中华人民共和国国土资源部. 全国地质灾害通报(2010年)[EB/OL]. [2011-05-03]. http://www.mlr.gov.cn/zwgk/zqyj/201101/P020110120670131247443.pdf.Ministry of Land and Resource of the People's Republic of China. Geological hazards bulletin of China (2010) [EB/OL].[2011-05-03]. http://www.mlr.gov.cn/zwgk/zqyj/201101/P02011.0120670131247443.pdf.

[2] 刘艺梁, 殷坤龙, 刘斌. 逻辑回归和人工神经网络模型在滑坡灾害空间预测中的应用[J]. 水文地质工程地质, 2010, 37(5):92-96.LIU Yi-liang, YIN Kun-long, LIU Bin. Application of logistic regression and artificial neural networks in spatial assessment of landslide hazards[J]. Hydrogeology & Engineering Geology,2010, 37(5): 92-96.

[3] 王卫东. 基于 GIS的区域公路地质灾害管理与空间决策支持系统研究[D]. 长沙: 中南大学土木工程学院, 2009: 114-128.WANG Wei-dong. Regional highway geological hazard management and spatial decision support system based on GIS[D]. Changsha: Central South University. School of Civil Engineering, 2009: 114-128.

[4] 王卫东, 陈燕平, 钟晟. 应用CF和Logistic回归模型编制滑坡危险性区划图[J]. 中南大学学报: 自然科学版, 2009, 40(4):1127-1133.WANG Wei-dong, CHEN Yan-ping, ZHONG Sheng. Landslides susceptibility mapped with CF and Logistic regression model[J].Journal of Central South University: Science and Technology,2009, 40(4): 1127-1133.

[5] 吴益平, 殷坤龙, 陈丽霞. 滑坡空间预测数学模型的对比及其应用[J]. 地质科技情报, 2007, 26(6): 95-100.WU Yi-ping, YIN Kun-long, CHEN Li-xia. Comparison and application of mathematics model of landslide spatial assessment[J]. Geological Science and Technology Information,2007, 26(6): 95-100.

[6] Catani F, Casagli N, Ermini L, et al. Landslide hazard and risk mapping at catchment scale in the Arno River Basin[J].Landslides, 2005, 2(4): 329-342.

[7] Fell R, Corominas J, Bonnard C, et al. Guidelines for landslide susceptibility, hazard and risk zoning for land-use planning[J].Engineering Geology, 2008, 102: 99-111.

[8] Dai F C, Lee C F. Landslide characteristics and slope instability modeling using GIS, Lantau Island, Hong Kong[J].Geomorphology, 2002, 42: 213-228.

[9] Wang W D, Xie C M, Du X G. Landslides susceptibility mapping in Guizhou province based on fuzzy theory[J]. Mining Science and Technology, 2009, 19(3): 399-404.

[10] Akgun A, Bulut F. GIS-based landslide susceptibility for Arsin-Yomra (Trabzon, North Turkey) region[J]. Environmental Geology, 2007, 51(8): 1377-1387.

[11] Akgun A, Dag S, Bulut F. Landslide susceptibility mapping for a landslide-prone area (Findikli, NE of Turkey) by likelihoodfrequency ratio and weighted linear combination models[J].Environmental Geology, 2008, 54(6): 1127-1143.

[12] 许冲, 戴福初, 姚鑫, 等. 基于GIS的汶川地震滑坡灾害影响因子确定性系数分析[J]. 岩石力学与工程学报, 2010, 29(增刊1): 2972-2981.XU Chong, DAI Fu-chu, YAO Xin, et al. GIS based certainty factor analysis of landslide triggering factors in Wenchuang Earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(Suppl 1): 2972-2981.

[13] 肖桐. 基于 GIS的兰州市滑坡空间模拟研究[D]. 兰州: 兰州大学资源环境学院, 2006: 39-45.XIAO Tong. GIS-based research on spatial simulation of landslide in Lanzhou[D]. Lanzhou: Lanzhou University. College of Resource and Environmental Science, 2006: 39-45.

[14] 丛威青, 潘懋, 李铁锋, 等. 基于GIS的滑坡、泥石流灾害危险性区划关键问题研究[J]. 地学前缘, 2006, 13(1): 185-190.CONG Wei-qing, PAN Mao, LI Tie-feng, et al. Key research on landslide and debris flow hazard zonation based on GIS[J]. Earth Science Frontiers, 2006, 13(1): 185-190.

[15] Ayalew L, Yamagishi H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan[J]. Geomorphology,2005, 65(8): 15-31.

[16] 张文彤, 董伟. SPSS统计分析高级教程[M]. 北京: 高等教育出版社, 2004: 163-188.ZHANG Wen-tong, DONG Wei. Advanced statistical analysis using SPSS[M]. Beijing: Higher Education Press, 2004:163-188.