一类非线性摄动问题解的渐近性态及其精度分析＊

范小笑，唐荣荣

（湖州师范学院 理学院，浙江 湖州313000）

0 引言

非线性摄动问题在自然科学甚至社会科学的众多领域中都存在着大量丞待解决的模型.利用现代数学的各种方法探索非线性问题解的存在性，寻求解的高精度近似表达式，一直以来都是数学和应用数学工作者极为关注的研究课题.近几十年来，国内外许多数学工作者致力于该方向的研究，应用摄动展开法、多尺度法、平均化法、匹配渐近展开法、重正规法、WKB方法等解决了大量的非线性问题［1～10］.值得注意的是以各个领域中的模型为背景的非线性问题研究，由于借鉴了模型所涉及领域的研究方法和相关结论，因此较有效地推进了摄动理论的发展，修正了原有的研究方法，扩大了研究结果的应用领域.以模型为背景，Holmes M H［1］、Bobkova A S［2］等对多维摄动系统的研究获得了进展，莫嘉琪［6］、唐荣荣［7～9］、韩祥临［10］等对一些类型的非线性摄动问题的可解性条件以及解的渐近性态进行了较深入的探索.

非线性摄动问题没有统一的求解模式和解的结构，当方程的结构或条件发生变更时，解的存在性、求解模式和解的结构往往都会有较大的变化.

文献［4］中，在利用压差阻力、浮力，用落球法精确测定重力加速度时，给出了一类二阶非线性方程：

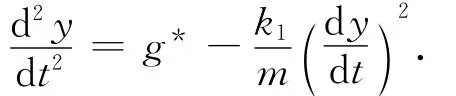
其中

文献［5］在考虑粘滞阻力的前提下，探讨了在空气中用落球法测定重力加速度问题，得出球体在空气中自由下落的方程为：

其中，k2＝6πηR，p，q＞0，g＊，k1同文献［4］.以上参数的物理意义详见文献［4］、［5］.考虑到当球体的半径大于0.01m时，0＜≪1，因此上述两个模型均可归类于非线性摄动方程：

其中 ，0＜ε≪1，p，q为正常数.

由于在空气中进行受力分析时经常需要考虑压差阻力与粘滞阻力，因此在物理模型中，经常需要求解与上述类型相关的方程.以下首先运用摄动理论讨论一类较文献［4］、［5］更广泛的非线性摄动初值问题，探讨其解的存在性以及解的渐近表达式.然后将结果应用于文献［4］、［5］中方程的求解并进行精度分析.

1 解的存在性和形式解

考虑如下一类非线性摄动初值问题：

且满足初值条件：

其中，0＜ε≪1.A（ε），B（ε）满足：A（ε）＝A0＋εA1＋ε2A2＋…B（ε）＝B0＋εB1＋ε2B2＋…

其中，A0，B0，A1，B1，A2，B2为常数.

且假设：

［H1］ f（y′；t；ε）有界，并且关于y′满足利普希茨条件；

［H2］ f（y′；t；ε）关于y′，t，ε任意阶可导，且任意阶导数都是域R×［a，b］×［0，ε0］上的连续函数，

其中ε0是一个适当小的正常数.

以下考虑其解的存在性以及表达形式.

设问题（1）～（3）式具有如下形式的渐近解：

由A（ε），B（ε）的表达式，有：

y（t0）＝A（ε）＝A0＋εA1＋ε2A2＋…

y′（t0）＝B（ε）＝B0＋εB1＋ε2B2＋…

把（4）式代入（1）式，得到：

由条件［H2］，将函数f （y0′＋εy1′＋O（ε2）；t；ε） 在ε＝0点Taylor展开，可得：

f （y′0＋εy1′＋O（ε2）；t；ε） ＝

把（6）式代入（5）式，得到：

比较（7）式中的ε同次幂系数，得到：

和

注意到方程（8）式可化为：

且在假设条件［H1］～ ［H2］下，f（z0；t；0）在域R×［a，b］上连续且有界，并且关于z0满足利普希茨条件，则根据文献［11］可知，∃δ＞0，且δ≤b－a，方程（12）式在｜t－t0｜≤δ上存在唯一解，于是问题（8）、（9）式在｜t－t0｜≤δ上存在唯一解.

我们不妨假设方程（8）、（9）式的解为y0，从而可知这时fy′′（y0′；t；0）为t的确定函数.因此，方程（10）为二阶非齐次线性微分方程.类似地，根据文献［11］，由条件［H2］知方程（10）、（11）式存在唯一解，记方程（10）、（11）式的解为y1.

令y1′＝z ，则方程（10）式可化解为：

由常数变易法可得方程（13）式的通解为：

这里C1由（9）式确定.

注意到条件［H2］，由（14）式得：

其中p（t）＝－fy′′（y0′；t；0），Q（t）＝fε′（y0′；t；0）.这里C2由（11）式确定.

将（13）式代入（4）式，可以知道满足假设条件［H1］、［H2］时的方程（1）式有以下形式的解：

其中C1、C2是由（9）和（11）式确定的常数.

综上所述，在满足假设条件［H1］、［H2］的情况下，原问题的解被唯一确定，且由（8）～（15）式问题（1）～（3）式解的渐近表达式（16）式被给出.

2 应用

为了说明以上所得渐近解（16）式的精确度，以下将利用上述结论（16）式对文献［4］、［5］中的模型求出相应的渐近解，然后进行精确度分析.

2.1 球体在空气中下落问题的渐近解

当原问题中f（y′；t；ε）＝εy′＋py2－q时，即为文献［4］、［5］中的球体在空气中自由落体的非线性问题：

易知问题（17）、（18）式有形如（4）式的解，且由（8）～（11）式可知，问题（17）式的退化方程为：

考虑到文献［4］、［5］模型中p、q的取值范围，由（12）知，方程（19）式有如下唯一确定的解：

从而

由（21）易得：

当t＝0时，y＝0.解得：

从而：

对于方程（20）而言，

于是（22）、（23）式得问题（17）、（18）式的渐近解为：

2.2 球体在空气中下落方程的精确解以及渐近解的精度估计

在方程（17）式中，设y′＝v，将方程转化为：v′＋εv＋pv2＝q.可得：

从而

两边积分，得：

当t＝0时，y＝0.解得：

从而

其中

由Taylor级数展开得到：

此外

由（27）、（28）式得：

将（26）～（29）式代入（25）式得到问题（17）、（18）式的精确解：

比较问题（17）、（18）式的渐近解（24）式与精确解（30）式，由前两项完全相同，可知两者误差的量级仅为O（ε2）.因此可知，在适当条件下可简捷地利用摄动展开法得到相关非线性问题的渐近解，当ε充分小时，可以达到足够高的精度.

3 结论

由上述讨论，得到：

结论1 在满足假设条件［H1］、［H2］的情况下，原问题（1）～（3）的解唯一存在，且其解的渐近表达式为：

其中p（t）＝－fy′′（y0′；t；0），Q（t）＝fε′（y0′；t；0），0＜ε≪ 1 .

当方程（1）式中f（y′；t；ε）＝εy′＋py2－q时，问题（1）～（3）即为文献［4］、［5］中的球体在空气中自由落体的非线性问题（17）、（18）式：

结论2 文献［4］、［5］中的球体自由落体模型（17）、（18）式的渐近解与精确解的一阶表达式完全相同，两者误差至多为O（ε2）：

其中p，q＞0，0＜ε≪1.

综上可知：摄动展开法是求解一些非线性摄动方程的一种有效方法，在适当条件下，可使渐近解的精确度达到足够的高度.因此，摄动展开法可以解决大量的物理模型的求解问题.由以上探讨可知，在条件［H1］、［H2］下，继续上述解法可求得原问题解的更高阶渐近展开式，使其渐近解具有更高的精度.

［1］Holmes M H.扰动法导论［M］.北京：世界图书出版公司，2003.

［2］Bobkova A S.The Behavior of Solutions of Multidimensional Singularly Perturbed Systems with one Fast Variable［J］.Ordinary Diff Eqs，2005，41（1）：22～32.

［3］Nayfeh A H .Problems in Perturbation［M］.New York：Johu，1985.

［4］俞晓明，崔益和，陈飞，等.考虑空气阻力、浮力用落球法精确测定重力加速度的研究［J］.物理与工程，2010，20（5）：26～28.

［5］周薇.流体的粘滞阻力对物体运动的影响［J］.技术物理教学，2009，17（2）：27～28.

［6］MO Jia－qi，LIU Shu－de.Asymptotic Behavior of Solutions for Reaction Diffusion Equations with Two Parameters［J］.Mathematic Application，2009，22（1）：42～47.

［7］Tang Rong－rong.The Asymptotic Behavior of Solution for a Class of Strongly Nonlinear Non－autonomous Equation［J］.Ann of Diff Eqs，2006，22（4）：569～572.

［8］Tang Rong－rong.The Shock Behavior for the Nonlinear Singularly Perturbed Two－points Boundary Value Problems［J］.Advances in Mathematics，2005，34（5）：497～502.

［9］Tang Rong－rong.Asymptotic Solution for a Class of Weakly Nonlinear Singularly Perturbed Reaction Diffusion Problem［J］.J Shanghai Univ，2009，13（1）：12～15.

［10］HAN Xiang－lin.The Asymptotic Behavior for a Nonlinear Singularly Perturbed System［J］.Chin Quart J of Math，2007，22（2）：175～178.

［11］王高雄，周之铭，朱思铭，等.常微分方程［M］.北京：高等教育出版社，2006.