基于层次分析与模糊综合评价的电视节目质量评价方法
丁汪,高福安
(中国传媒大学,北京100024)
1 引言
收视率、投入产出比是从定量的方面,分别从受众市场和财务运营情况来对节目质量进行的评价,这已成为电视行业和广告主的通常做法,他们分别反映的是受众收看节目的时长和对资本的运用状况来衡量节目质量的考核依据。但这样并不是节目质量评价的客观标准,如对一些纪实新闻、纪录片等节目的收视率与投入产出比往往是比较低的,但此类节目品味却很高,所带来的社会影响是很广泛的,在社会效应方面就更为重要。因此目前许多国家,特别是发达国家,为了弥补收视率和投入产出比指标的单一,不能反映节目品质等缺点,引入了舆论导向、节目内容、表现形式、主持人风格、节目反响等定性指标[1]。
对于上面的那些定性指标提供了从不同角度去评价节目质量的好坏。舆论导向是从国家的角度,节目内容、表现形式、及主持人风格是从节目本身的角度出发,而节目反响是从社会上普通人和专业人士的角度去评价,再加上以前固有的收视率和财务指标,综合以上所有的指标,将从全方位去反映一个节目的质量。
但是那些定性的指标本身就是个模糊的概念,是各方面受众对节目各要素感知与自己的心理预期做的比较。这些都是定性的指标,在对节目质量评价时,要将这些定性指标转化为定量指标,这就本文主要介绍的方法:将待评价的节目指标(定性与定量)转换成隶属度矩阵,再通过层次分析方法得到各因素的权重向量,从而建立多层次模糊综合评价模型,利用模糊数学原理评价出各节目质量基于各评价指标的综合优越度。
2 电视节目质量综合评价指标的构建
电视节目质量评价是一个系统的工程,建立评价指标体系是进行评价的基础工作,其科学性和合理性直接影响着评价结果的准确性。在评价指标体系中,既有定量化因素,又有定性化因素,却他们相互影响、相互制约。评价指标选择的原则是以尽量少的指标,反映最主要和最全面的信息[2]。利用层次分析方法基本原则,建立节目质量综合评价指标体系如下表1:

表1 节目质量综合评价指标体系

续表
给出评语集 V={v1,v2,v3,v4,v5}={很差,差,一般,好,很好}。须指出的是,在具体综合评价过程中,应根据要求对这些指标有所删减。
3 层次分析方法确定评价指标的权重
3.1 层次分析法概念
层次分析法(AHP)是美国运筹学家沙旦(T.L.Saaty)于20世纪70年代提出的一种定性与定量相结合的决策分析方法,它常常被运用于多目标、多准则、多要素、多层次的非结构化的复杂决策问题,特别是战略决策问题的研究,具有十分广泛的应有性。
AHP决策分析法,是一种将决策者对复杂问题的决策思路过程模型化、数量化的过程。通过这种方法,可以将复杂问题分解为若干层次和若干因素,在各因素之间进行简单的比较和计算,就可以得出不同方案重要性程度的权重,从而为决策方案的选择提供依据。
3.2 层次分析法的基本步骤
第一,建立层析结构模型
对社会系统进行调查研究,将目标准则准则体系所包含的因素划分为不同层次,如目标层、准则层、方案层等,构成递阶层次结构模型。用不同的形式框标明层次的递阶结构和元素的从属关系,应该突出重点,抓住关键因素,第一层元素不易过多,AHP方法对于序列型和非序列型层次结构都是适用的。
第二,构造判断矩阵
按照层次结构模型,从上到下逐层构造判断矩阵。每一层元素都以相邻上层次各元素为准则,按1-9标度方法(如表2)两两比较构造判断矩阵(如表3),也可以通过其他改进的方法构造。
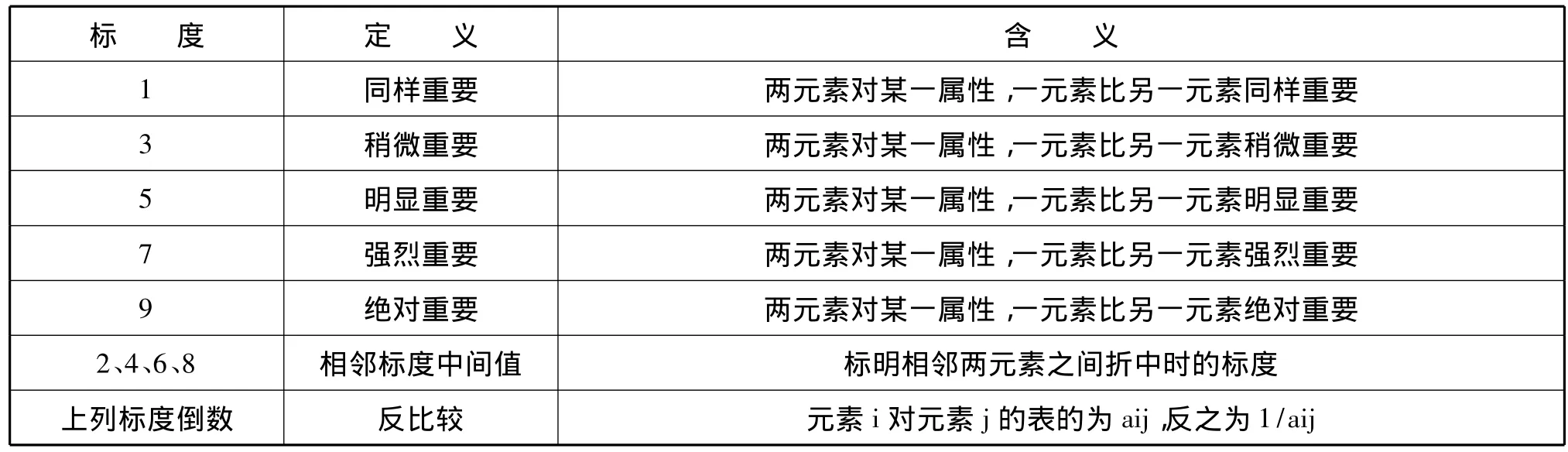
表2 1-9标度方法

表3 判断矩阵
第三,层次单排序及其一致性检验
根据实际情况,用不同方法求解判断矩阵最大特征值相对应的特征向量,进过归一化处理,既得层次单排序权重向量。层次结构复杂,每一层次元素较多,宜采用根法在计算机上计算,也可以应用APH软件。
(1)计算A的每一行元素之积
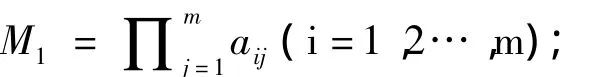
(2)计算Mi的m次方根
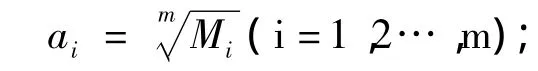
(3)对向量 ai={a1,a2,…,am}作归一化处理
Wi=ai/∑mk=1ak(i=1,2…,m);
得到最大特征值对应的特征向量Wi
(4)求A的最大特征值λ。由于AW=λW,因此

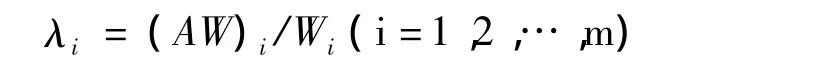
(5)判断矩阵的一致性检验
判断矩阵是分析者凭个人知识及经验建立起来的,难免存在误差。判断矩阵的一致性检验公式C.R=C.I/R.I其中C.I=(λ-m)/(m-1);m为判断矩阵的阶数;R.I为平均随机一致性指标(如表4)C.I<0.1时,一致性通过。

表4 平均随机一致性指标
第四层次总排序及其一致性检验
设相同两层次中,层次A有m个元素,层次B有n个元素,上一层次元素总排序权重为w,下一层元素关于上一层次元素Aj的层次单排序向量为(b1j,b2j,…,bnj),层次B的总排序权重值由表5列出。
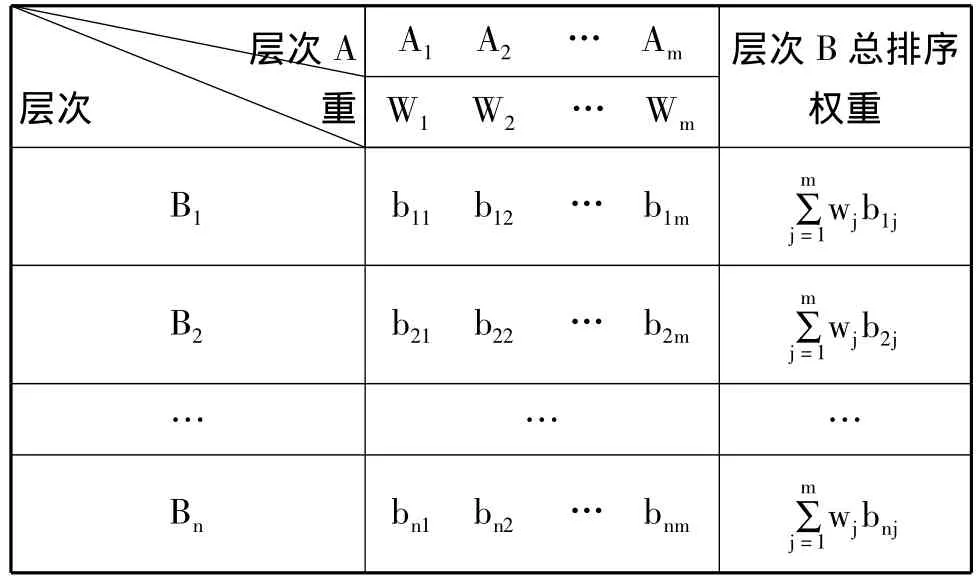
表5 总排序权重值
应该注意,在实际操作中,总排序一致性检验往往可以省略,因为单排序一致性检验通过,总排序也通过[3]。
3.3 以新闻节目质量中〈节目反响U5〉层次分析评价为例
判断矩阵如下表6:(注:对于不同的节目其判断矩阵不同)。
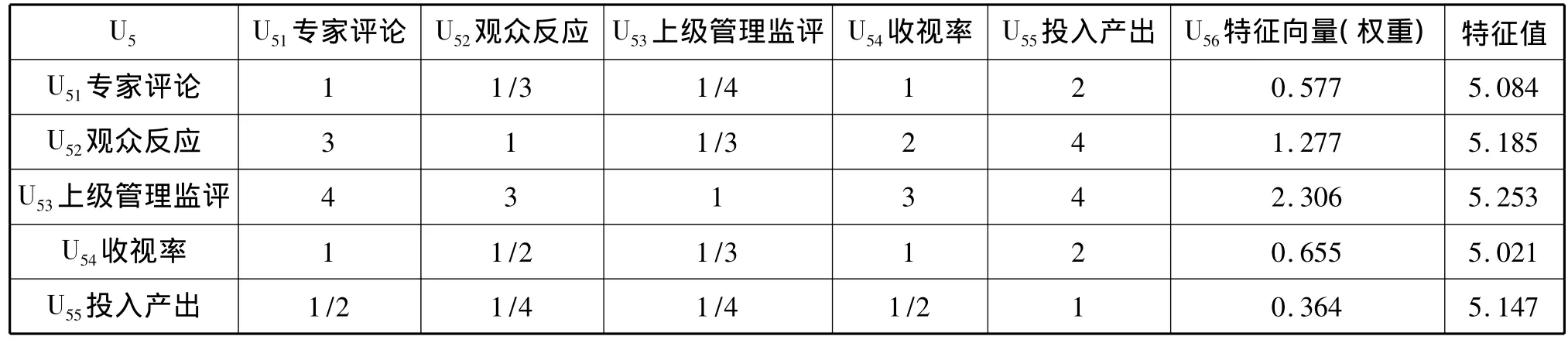
表6 判断矩阵
则最大特征向量λ=5.138158 W4={0.577,1.277,2.306,0.655,0.364}
一致性检验C.I=0.138/4=0.035;CR=0.035/1.12=0.031<0.1所以满足一致性。
由此可以看出在新闻节目中,各因素相比较,上级管理监评的权重最大,而投入产出考虑的比较小。
4 模糊综合评价
4.1 模糊评价概念
20世纪80年代初,汪培庄提出了综合评判模型,此模型以它简单实用的特点迅速波及到国民经济和工农业生产的方方面面,广大实际工作者运用此模型取得了一个又一个的成果。与此同时,还吸引了一些理论工作者对此模型进行深化和扩展研究,出现了一批诱人的成果,诸如:多级模型、算子调整、范畴统观等等。而且,针对实际应用中模糊综合评判模型常遇到的一些问题,对其进行了改进,可采用多层次模糊综合评判模型和广义合成运算的模糊综合评判模型。
模糊综合评价法是一种基于模糊数学的综合评标方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解
对一个事物的评价,常常要涉及多个因素或者多个指标。比如,要判定节目质量的好坏,每个人都可从不同角度考虑:有人看主持风格,有人看节目效果,有人看舆论导向,这时就要根据这多个因素对事物作综合评价。具体过程是:将评价目标看成是由多种因素组成的模糊集合(称为因素集u),再设定这些因素所能选取的评审等级,组成评语的模糊集合(称为评判集v),分别求出各单一因素对各个评审等级的归属程度(称为模糊矩阵),然后根据各个因素在评价目标中的权重分配,通过计算(称为模糊矩阵合成),求出评价的定量解值。上述过程即为模糊综合评判。
4.2 模糊综合评价的步骤
模糊数学的综合评判主要涉及4个要素:因素集U;方案集A;隶属矩阵R和权重分配向量W。根据评价指标的不同,模糊综合评判可分为一级模糊评价和多级模糊评价。这里研究二级模糊评价。
(1)建立因素集U和次因素集
设因素集 U={U1,U2,…,Um},第二层次因素子集可表示成m维“向量”形式:Uij={Ui1,Ui2,Ui3,…,Uim}其中 UJk(k=1,2…,m)是第 j次因素集在主因素Ui上的反应。Uij可以是数量,也可以是一种自然语言的定性表述,就比如对节目质量的定性描述,则Uij为集合中的方案且为U上的模糊子集[4]。
(2)建立评价指标的评语集
根据评价等级及其相应标准,给出评语集V={v1,v2,v3,v4,v5}={很差,差,一般,好,很好}={1,2,3,4,5},1-5 为等级高低量度,是对模糊评语{很差,差,一般,良好,优秀}进行的量化处理。
(3)建立因素集U的各因素权重集W
用上述的层次分析法确定因素的权重集W。因素权重集W={W1,W2,…,Wm}是指各因素对于拟选定方法而言的重要性及影响程度,且要求满足0<Wk<1,∑mk=1Wk=1。
(4)隶属矩阵的确定
定量指标的隶属度由隶属函数法确定,非定量指标采用单因素评价法确定。设第i个因素的单因素模糊评价为 Ri={ri1,ri2,…,rim}(i=1,2,…,n),其中rij表示第i个因素对第j个评语的隶属度,ni个模糊向量R1,R2,…,Rni构成从U到V的模糊矩阵为

(5)综合评判
由隶属矩阵R以及因素权重W,对第二层次每个Ui的ni个元素进行综合评价。Ui中各因素的权向量为 Ai={Ai1,Ai2,…,Aimi};综合评价矩阵为 Rj,于是综合评价向量:Bi=Ai。Ri={ai1,ai2,…,ain1合成运算)由此类推,进行第一层次各子集的综合评价.在第一层次将子集Ui当作一个因素,第二层次综合评价向量作为的单因素评价,最后将得到总的综合评价。
4.3 以新闻节目质量中<节目反响U5>模糊评价为例
设每个次因素有5个人对节目反响进行单因素评价如表7。
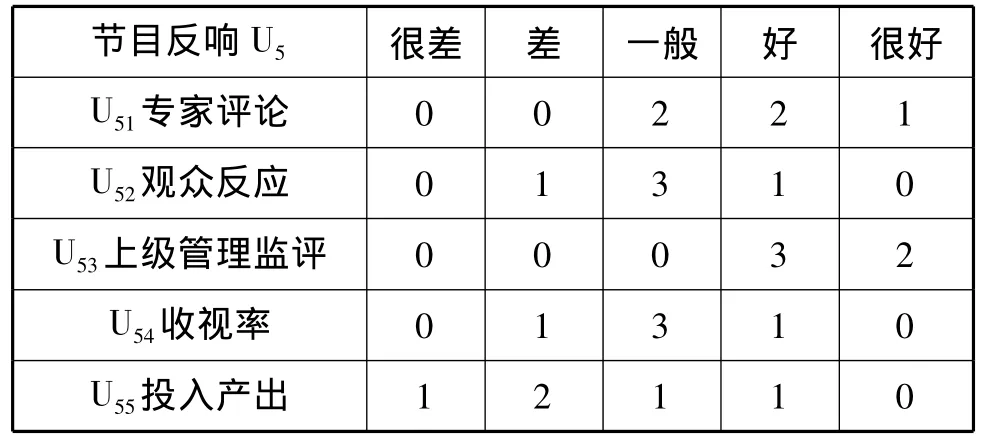
表7 单因素评价
对每个次因素标准化得模糊矩阵:

则评价向量 B5=W5R=(0.73,0.53,1.46,2.07,1.04),这将作为下次节目反响的单因素评价。
5 总结
a.根据层次分析法基本原理建立了节目质量综合评价指标,并利用层次分析法可以计算指标权重,并通过判断矩阵一致性检验确定合理的权重向量。
b.在对节目指标计算权重的时候好充分根据所评价的节目类型,合理进行评价。
c.运用层次分析法和模糊数学理论对节目质量标准进行了综合评价和模糊综合评判选择,避免了因素过多而难于分配权重的弊端,也避免了单因素决策的片面性和人们主观认识差异所引起的决策失误,特别是在各种影响方案选择的指标出现优越性交叉时,能够做出更为科学、准确、有理论依据的判断。同时,该种综合评判模型也可用于其他系统工程的多方案优先中。
[1] 王云峰.浅谈电视节目新型评价体系的构建[J].管理透视-电视研究.
[2] 李俊芳,吴小萍.基于AHP—FUZZY多层次评判的城市轨道交通线网规划方案综合评价[J].武汉理工大学学报,2007,4(2):205-208.
[3] 郭立夫李北伟.决策理论与方法[M].北京:高等教育出版社,2004.
[4] 罗一忠,吴爱祥,胡国斌.采场人-机-环境系统可靠性模糊综合评价[J].中南大学学报(自然科学版),2006,37(4):804-809.

