基于星座图扩张算法的MIMO-OFDM空时分组码译码方案

崔天晓，孟春雷，蔡超时，冯晓宁，胡峰

(1.中国传媒大学，北京100024;2.交通运输部公路科学研究院，北京100088)

1 引言

MIMO(Multiple Input Multiple Output，多输入多输出)技术多被用于发射链路和用户终端设备，以此实现发射分集(transmit diversity)并获得较高的传信率［1］。空时编码(The space-time coding，STC)技术主要目的是用来提高分集增益(diversity gain)。分集指的是相同的信息编码之后通过不同的天线进行发射，然后将所有天线系统的接收值进行联合译码，以此用来增强信号的可靠性。空间复用(Spatial Multiplexing，SM)技术可获得较大的信道容量的自由度并提高频带的利用率。通过将数据复用成并行传输模式并通过不同的发射天线发射出去以此提高信道容量［2］。这些技术的性能依赖于通过信道估计所获得的收发天线之间的信道状态信息。MIMO系统虽然在一定程度上可以抗多径衰落，但是无法处理在高速移动条件下的频率选择性衰落。而MIMO和OFDM技术的结合可以很好的解决以上的问题。MIMO-OFDM利用了时间、频率、空间的三种分集技术，使无线系统对噪声、干扰、多径的容限大大增加。而且当信道情况好转时，可以使用空间复用的编码方式，成倍的提高传输速率。

总的来说，在多天线信道中，空时分组码(the space time block coding，STBC)是在MIMO信道方式下用来获得高数据率的技术中最普遍的技术之一［3］。由于其允许在基站上放置多路天线，而且空时编码的结构极其简单便于实现，所以应用最为广泛。文章［4］给出的正交空时编码算法的译码方案正式基于最小欧氏距离来判决误比特率，以此实现最大似然译码。最大似然译码的结构相对简单，但是实际的应用时还是存在诸多的困难。在瑞利准静态衰落通道中，译码部分含有信道系数叠加项，较大的值使得欧氏距离判决方案产生失真，当衰落系数统计量变大时这种失真尤为严重。

于是本文提出了一种基于星座图扩张技术的最大似然译码算法，以此增强欧氏距离判决的敏感度，并大大化简了译码的复杂度。这种算法主要适用于信道相关系数统计值偏大，而普通的译码算法严重失真的情形。特别需要指出的是，通过LS信道估计可以估计出准确的信道状态信息，以此来确定星座点的扩张系数，并通过线性放大将原始星座点移到相应的扩张区域中。在调节趋于最小欧氏距离的同时，最大似然译码也得以修正。复正交空时分组码可以在3根和4根发射天线系统中获得1/2的码率，本文的译码算法将在这两种空时编码方式下实现并进行仿真结果分析。

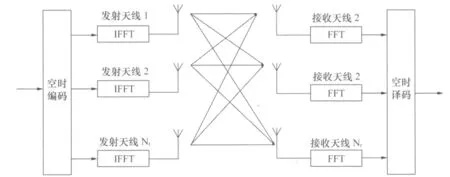
图1 MIMO OFDM系统模块结构图

2 MIMO-OFDM系统模型

2.1 系统模型

MIMO-OFDM(Multiple Input Multiple Output Orthogonal Frequency Division Multiplexing)指的是正交频分复用多输入多输出系统。图1给出了一个MIMO-OFDM系统的一般结构框图。

设定MIMO系统采用Nt根发射天线和Nr根接收天线。MIMO信道模型定义为Nr×Nt瑞利准静态衰落信道。由特定的编码矩阵描述(Nt，L，k)空时分组码结构，其中L指的是时隙数［1］，k指的编码携带的符号数。这里空时分组码的码率等于r=k/L。

Nt输入/Nr输出的信道矩阵可表示为:

其中hi，j指的是从第j个发射天线到第i个接收天线之间的衰落系数。假设hij是相互独立复高斯分布，具备均值为零方差不恒定的特点。MIMO信道在本论文中始终被假设为准静态衰落，在L长度的时隙内恒定不变，但是帧长度内是不断变化的。可以假设它表示的是一种室内信道，其时间变量为常数并且相对于突发性数据的时间其变化是可忽略的［5］。

假定接收端可以精确的同步，t时第i根天线上的接收信号 rt，i表示如下:

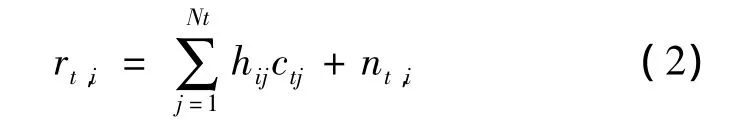
式中的噪声样本nt，i是相互独立的复高斯随机变量，均值为零，方差为，可表示为 CN(0，)。

方便起见，将(2)中的下标去掉，这样接收到了空时信号矩阵就可以表示为:

其中 H ∈CNr×Nt，r∈ CNr×L，Xc∈ CNr×L和 n ∈Nr×L

3 空时分组码解码优化算法

现有的复正交空时编码算法可以在线性接收过程中获得全分集增益。这里主要关注1/2码率的复正交空时分组码，改编码结构为首先传输码率为1的空时编码，结合共轭变换之后的编码实现复正交结构的编码方式［6］。这一部分将介绍如何利用星座扩张方案来优化最大似然译码的1/2速率正交空时分组码。

3.1 正交空时分组码

对于Nt=3根发射天线和Nr根接收天线模式，构造1/2速率和3Nr分集增益的分组码。

这种码每8个时隙发送4个符号，其码率r=k/L 为［7］。在文献［8］中，分别用(5)(6)(7)和(8)公式给出了判定x1，x2，x3，x4的判决统计值。

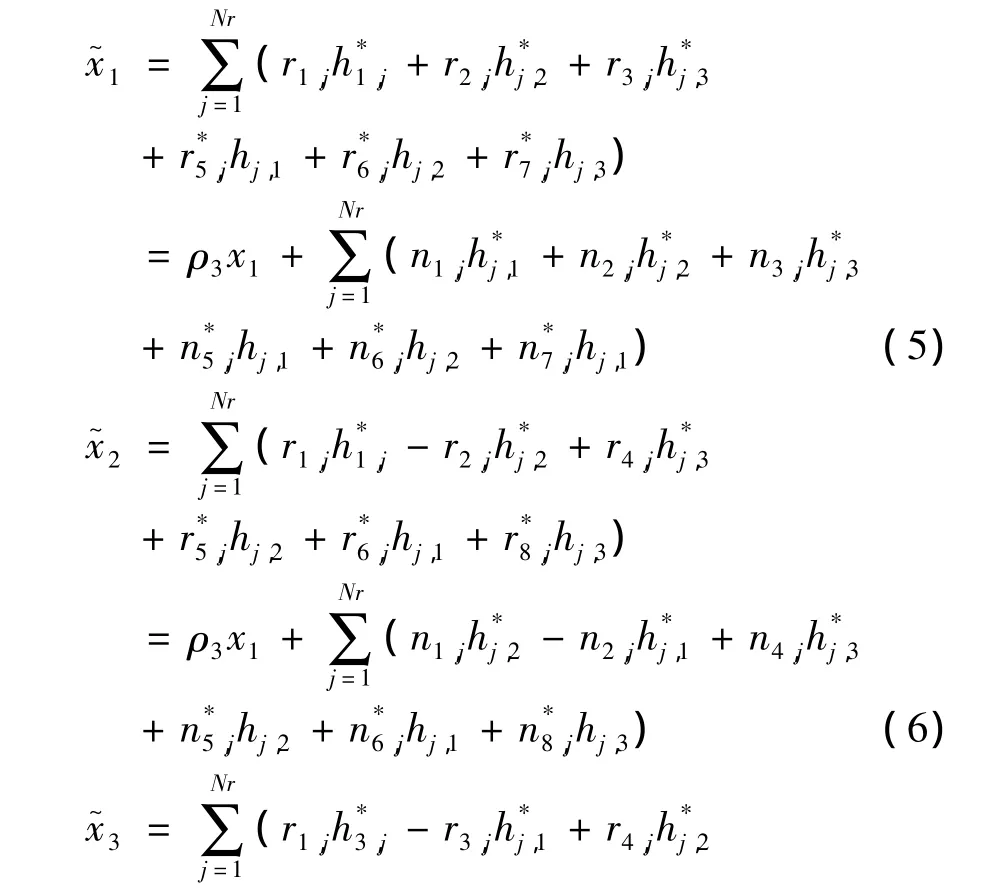
上式中ρ3表示为:

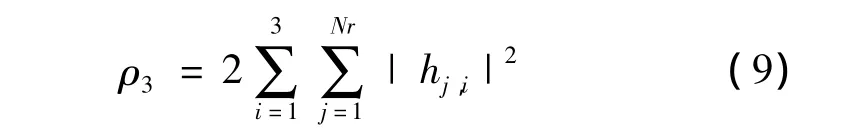
4根发射天线的1/2码率/4Nr分集增益的正交空时分组码为:

对于译码，则由公式(11)(12)(13)和(14)分别给出 x1，x2，x3和 x4的判决统计值。

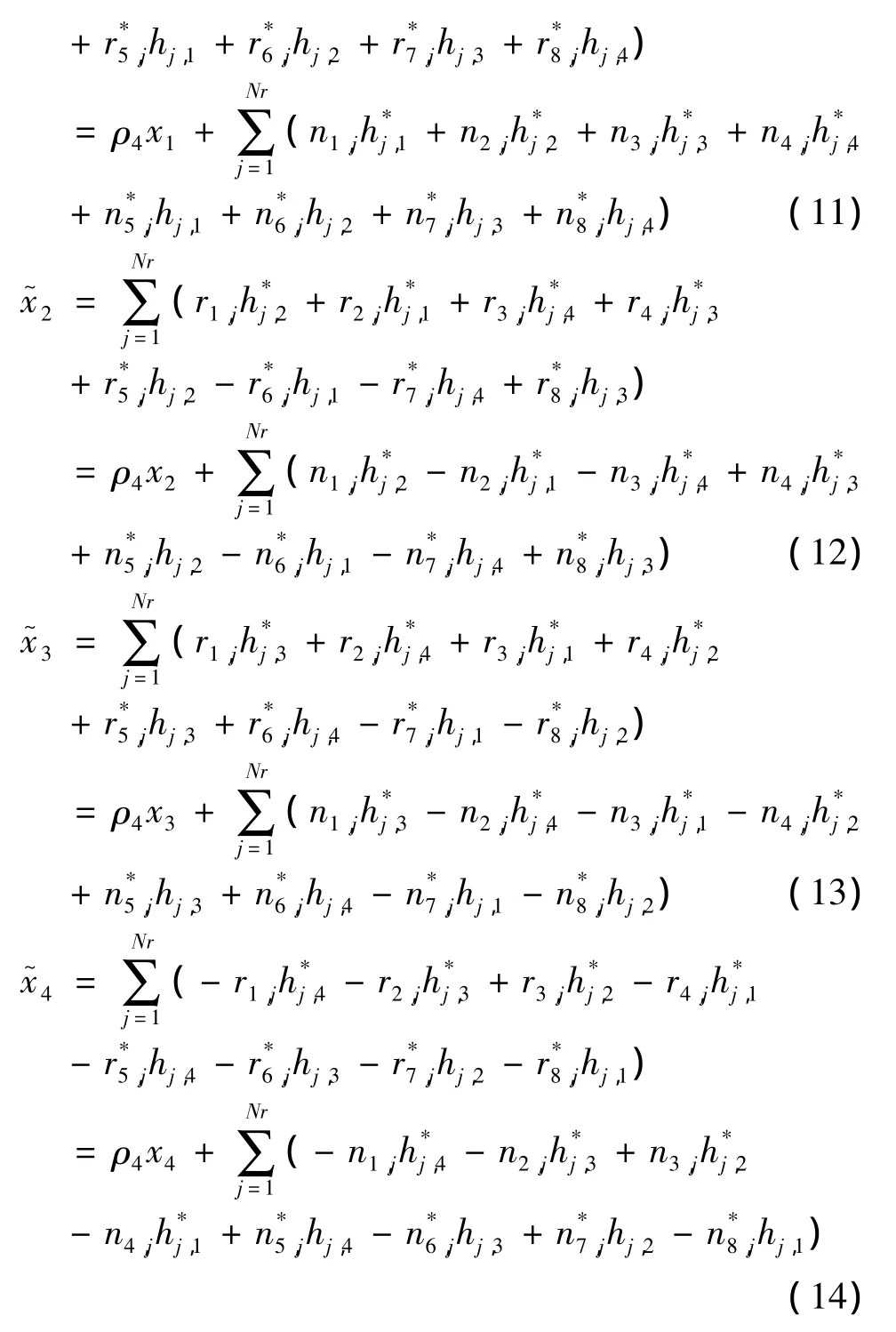
上述的由下列式子表示:

对最大似然译码而言，译码的过程就是选取所有可能值xi中(16)式给定的判决准则的最小值。

对于1/2码率的空时分组码来说，最小判定值就是最小欧氏距离，定义如下:

从(5～8)和 (11～14)的式子中，可以推导出如下的xi译码判定准则:

假定信道为准静态衰落并且ρk远大于1，这时很难获得准确的值，也就是说最大似然译码的方法在此情况下特别是在平坦衰落的信道中并不适用。这里给出了一种方法来改良最大似然译码的这种缺陷。

3.2 基于星座扩张的最大似然译码

在上述概念的基础上，本文设计了一种基于星座扩张的最大似然译码方案。有效的星座扩张方案可以将最小欧氏距离减小到最低值。这里选取等幅的星座调制方式，图2中给出的QPSK和8PSK调制下的星座扩张图，采用QPSK调制的情况时有4个星座点，满足 ，分别是 x1，x2，x3和 x4，每个星座点对应的扩张星座点分别为x'1，x'2，x'3和 x'4。比较 xi和x～i可以发现，扩张之后的星座点更接近统计判决值。通过采用有效星座扩张技术，可以表述为:

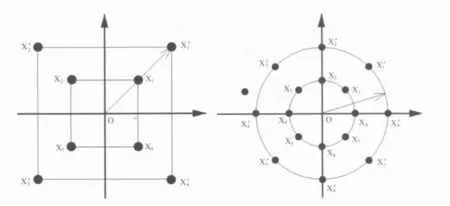
图2 QPSK和8PSK调制下的有效星座扩张图示

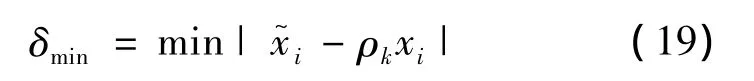
4 LS信道估计

信道状态信息的获得对于译码和信道的均衡至关重要。在选取了基于训练序列的MIMO信道估计最常用的LS信道估计法。

在N个传输数据中，前N-L个数据作为前导数据{x(1)，x(2)，...，x(N-L)}，并且令 rp=［rp(1)rp(2)，....，rp(N-L)］，Xp= ［x(1)，x(2，)，...，x(N-L)］。

MIMO系统模型如下所示:

其中 H∈CNr×Nt，rp∈CNr×(N-L)，Xp∈CNt×(N-L)和np∈CNr×(N-L)。

通过式子(21)可以很容易得到 LS信道估计［9］:

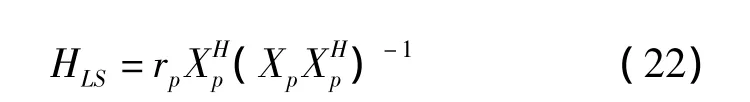
评估时仅仅利用接收到的信号和训练序列进行估计。LS差错准则最小均方误差函数(MSE)由下式给出:

5 仿真实验以及结果

本节将给出由式子(20)中译码方法所对应的仿真实验的结果(Xc3和Xc4)。在所有的仿真方案中，都把信道看作是瑞利准静态衰落信道，仿真图中描绘了误比特率BER与信噪比SNR之间的函数关系。设置接收天线个数Nr分别为1，2，3，4，并分别选取QPSK，8PSK，和16-QAM调制方式。每个样本均采用了105的数据量进行仿真。

固定Nt=3，令Nr从1变到4的仿真BER曲线如图3所示。由实验结果可以看出，对于同样的Nr，BER性能由好到坏依次为QPSK，8PSK和16-QAM调制模式所对应的曲线;而固定星座调制时，随着Nr的减小，BER性能也是逐渐恶化的。

图3 当Nt=3时，正交空时分组码的BER曲线

图4给出了当Nt=4时与Nt=3时相类似的仿真结果(Xc4)。各个模式的BER性能和图3中的类似。但是Nt=4的性能在相应的模式下要优于Nt=3的情况，这表明较高的分集增益对应较高的BER特性。

图4 当Nt=4时，正交空时分组码的BER曲线

6 结论

本文针对1/2码率的空时分组码所采用的最大似然译码，针对3根发射天线(Xc3)和4根发射天线(Xc4)的MIMO-OFDM系统进行了译码性能上的优化。这里假定传输信道为准静态衰落的MIMO信道，在这种情况下如果采用传统的最大似然译码，特别是在判决统计值很大的时候，欧氏距离值也许会劣化地十分严重。本文中给出的基于星座扩张技术的最大似然译码过程，用自适应的方式改良了最大似然译码算法中最小欧氏距离选项。仿真结果证实了这种星座扩张最大似然译码在瑞利准静态衰落信道条件下的有效性和可行性。

［1］ S K Mohammed，A Zaki，A Chockalingam，B S Rajan.High-Rate Space–Time Coded Large-MIMO Systems:Low-Complexity Detection and Channel Estimation［J］.Ieee journal of selected topics in signal processing，2009，3(6):958–974.

［2］ J T Wang.Throughput-Based Switching Between Diversity and Multiplexing in MIMO Systems With Cochannel Interference［J］.Ieee transactions on vehicular technolog，2009，58(7):3850–3855.

［3］ M Samuel，M Fitz.Multi-Strata Codes:Space-Time Block Codes with Low Detection Complexity［J］.Ieee transactions on communications，2010，58(4):1080-1089.

［4］ V T，Hamid Jafarkhani，A R Calderbank.Space–Time Block Codes from Orthogonal Designs［J］.Ieee transactions on information theory，1999，45(5):1456-1467.

［5］ G Foschini，M Gans.On limits of wireless communications in a fading environment when using multiple antennas［C］.Wireless personal communications，1998，6(3):311 – 335.

［6］ O Tirkkonen，A Hottinen.Square-Matrix Embeddable Space-Time Block Codes for Complex Signal Constellations［J］.Ieee transactions on information theory，2002，48(2):384-395.

［7］ Luis Miguel.MIMO Space-Time Block Coding(STBC):Simulations and Results［J］.Ece6604:personal＆ mobile communications，cortes-pena，Presented to DR.GORDON STUBER，2009:1-8.

［8］ Branka Vucetic，Jinhong Yuan.SPACE-TIME CODING，John Wiley ＆ Sons［J］，2003.

［9］ H Nooralizadeh，SS Moghaddam.A New Shifted Scaled LSChannel Estimator for Rician Flat Fading MIMOChannel［C］.2009 IEEE Symposium on Industrial Electronics and Applications(ISIEA 2009)，Kuala Lumpur，Malaysia，2009，1:243-247.