双臂轴支架的剖面形状和安装角度对船舶伴流场的影响
王展智 熊 鹰 刘志华 姜治芳
1海军工程大学船舶与动力学院,湖北武汉430033 2中国舰船研究设计中心,湖北武汉430064
0 引 言
轴包套和轴支架是为便于螺旋桨在船艉的安装而设计的附体形式。由于船体、轴包套和轴支架等复杂的曲面形状在船体艉部形成了十分不均匀的三向伴流场,使得螺旋桨的叶剖面在一周之内可能处于大攻角高进速甚至是负攻角的情况下工作,从而产生严重的空泡和振动现象[1],这对螺旋桨的性能是十分不利的。让附体与船体产生有利的干扰,一直是造船工程师追求的目标。
近年来,随着数值计算方法的不断发展和计算机能力的不断提升,开始越来越多地采用CFD方法研究带附体船舶的伴流场。黄胜和单铁兵[2]采用RANS方法分析比较了带附体(轴包套、轴支架、呆木和舵)的和裸船体的艉流场,结果表明,附体对桨盘面处的伴流有影响,特别是在支架周围,由于轴包套和轴支架的存在,带附体船舶桨盘面处的轴向伴流变大,并出现了较大的伴流峰,脉动量大。常煜等[3]研究了含附体水面船模的粘性流场数值计算的分块结构化网格划分方法,并将计算得到的流场细节与试验值进行了比较,吻合较好。Bjorn 和 Nicolas[4]运用数值计算软件 SHIPFLOW,基于重叠网格技术,研究了全附体实尺度和模型尺度船舶带自由液面的绕流问题,经与实船实验数据相比,计算结果在阻力、波形、压力和速度分布等方面还有待提高,但船模计算结果比较理想。当对附体与船体相互干扰的机理认识越来越成熟时,研究者开始将目光投向如何利用这种相互干扰。毕毅等[5]对双尾鳍与轴支架对排水型船的操纵性影响进行了试验研究;王展智等[6]比较了3种艉部附体方案的粘性阻力特性,得到了一些有意义的结论。
轴支架有两个比较重要的设计参数:支架剖面形状和支架安装角度。本文将通过数值方法,不考虑自由液面的影响,以某大型四桨水面船舶为研究对象,对双臂轴支架剖面形状和安装角度对船舶粘性阻力和螺旋桨盘面伴流场的影响进行研究。
1 数学模型
1.1 控制方程
雷诺平均N-S方程(式中变量都是时历平均值):

式中,ρ为流体密度;p为静压;fi为单位质量的质量力;ui,uj为速度分量;为代表湍流效应的雷诺应力项。
不可压缩粘性流体的连续性方程:

为了求解RANS方程中增加的雷诺应力,需要额外增加方程,使雷诺应力中的脉动值与时均值联系起来,以使方程组封闭,即湍流模型。而湍流的内在机理并未真正被人们所了解,迄今为止,还尚未认定一种解决湍流问题的最佳方法[7]。本文采用的湍流模型为RNG k-ε模型,这种湍流模型是标准k-ε模型的改进形式,它修正了湍动粘度,考虑了平均流动中的旋转及旋流流动情况,增加了反映主流的时均应变率[8]。该模型是一种适于计算船舶流场的湍流模型,本文仅给出了其基本形式,具体推导过程见参考文献[9]。方程形式如下所示。
湍流脉动动能方程(k方程):

湍流能量耗散率方程(ε方程):

式(3)~式(4)中,μt为湍动粘性系数,;Pk为湍动生成项,Pk=μtS2,其中为平均应变张量,;Rε为RNG k-ε模型特有的控件,,其中。以上式中的常数分别为σk=1.39,σε=1.39 ,Cε1=1.42 ,Cε2=1.68 ,Cμ=0.084 5,η0=4.38,β=0.012。
1.2 计算对象
本文的研究对象为排水型水面船舶,有球鼻艏。模型设计水线长LWL=8m,吃水d=0.269m,航速 v=4.385m/s,即 Fr=0.280。
该船为四桨推进,左右两侧各两个桨,每一侧均有两套轴包套和轴支架组合,根据其与船艏的相对位置,命名为外前桨轴包套和支架以及内后桨轴包套和支架,支架为双臂轴支架。其中,左、右舷的轴包套和双臂轴支架组合沿船体中纵面完全对称,但对于在单侧的外前桨和内后桨轴包套,虽然其形状不同,但却是固定不变的,因此本文不考虑它们的形状、位置或安装角度的变化。外前桨与内后桨的双臂轴支架的剖面形状完全一样,只是安装角度不同。船体、轴包套、双臂轴支架的整体模型轮廓如图1所示。
首先,对方案1(原始形状和安装角度)进行整体建模,计算其粘性流场,从而得到双臂支架前方的来流角度;然后依据该来流角度调整双臂轴支架的安装角度,以使其前方来流攻角为0,即方案5;最后,依据方案5设计出多种双臂轴支架剖面形状与安装角度组合的计算方案,如表1所示。表中角度为负表示与方案1的安装角度相反。
原始双臂轴支架的剖面形状(剖面形状1)和安装角度(方案1)如图2、图3所示,方案5外前桨双臂轴支架的安装角度如图4所示。其中,双臂轴支架剖面形状2由形状1的最大厚度位置前移10%弦长得到;双臂轴支架剖面形状3由形状1的厚度减半得到(图2)。

图1 计算模型的轮廓图Fig.1 Computationalmodel

图2 双臂支架的剖面形状Fig.2 Twin bracketsection profile

图3 方案1外前桨双臂轴支架的安装角度Fig.3 Twin shaftbracket installation angle of the forward propeller in Scheme 1

图4 方案5外前桨双臂轴支架的安装角度Fig.4 Twin shaftbracket installation angle of the forward propeller in Scheme 5

表1 不同双臂轴支架设计方案Tab.1 Different tw in shaft bracket schem es
1.3 网格划分及离散方法
本文的计算模型包括了轴包套、双臂轴支架和轴等附体,由于这些附体具有独立的几何形状,而且它们与船体曲面相交产生了复杂的交贯线,因此,在这种情况下,要构建满足一定分辨率的单块网格结构系统根本不可能。针对不同附体的形状和它们与船体曲面相交位置的特点,本文首先建立了许多结构、非结构组合网格分块,然后,运用网格对接技术将这些分块组合成完整的计算模型。整个计算流域共划分了48个分块,块与块之间通过交界面(interface)连接,共有约450万网格单元,船体壁面第一层网格的y+处于100~150之间。船体带附体的艉部网格划分情况如图5所示。

图5 艉部附体的表面网格Fig.5 Surfacemesh of the stern
1.4 边界条件及流域
由于计算对象的对称性,将仅考虑模型的右舷部分。计算流域如下:流体入口离船舶艏端一倍船长,流体出口离船舶艉端两倍船长,流体外边界离船体中纵剖面一倍船长。边界条件设置如下:上游入口采用速度入口,给定均匀来流的速度值;下游出口采用压力出口;上边界、侧边和中间面均采用对称面边界条件;在裸船体、轴包套和轴支架的表面定义无滑移、不可穿透的边界条件。采用有限体积法离散控制方程和湍流模式,对流项和扩散项采用二阶迎风格式进行离散,压力速度耦合迭代采用SIMPLEC方法。
2 结果及分析
9种双臂轴支架方案的船舶带附体粘性阻力计算结果如表2所示。
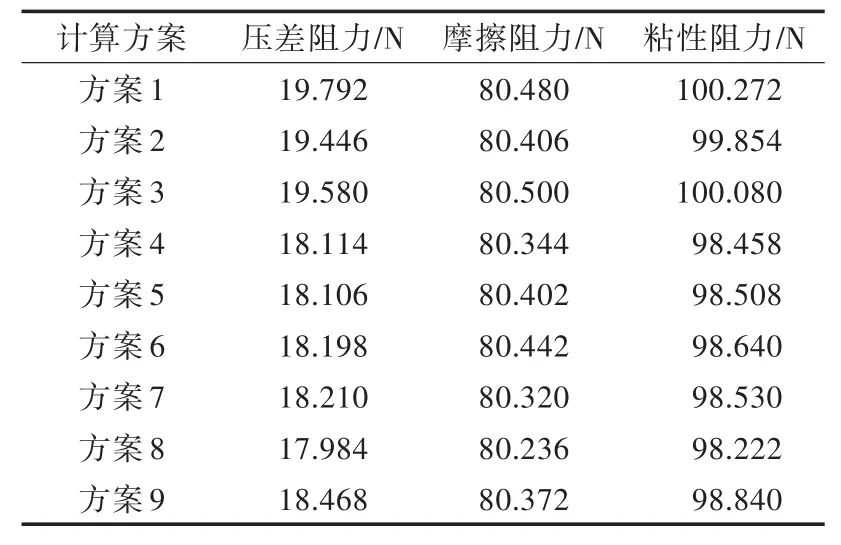
表2 不同双臂轴支架方案的船舶粘性阻力Tab.2 Viscous force of the 9 tw in shaft b racket schem es
由表中可看出:
1)方案2和方案3的船舶粘性阻力比方案1(原始双臂轴支架方案)的略小,相对减阻率(与方案1比较)不到0.45%,可见双臂轴支架的剖面形状对船体总的粘性阻力影响较小。
2)方案4~9均改变了双臂轴支架的安装角度,其中相对减阻率最低的是方案9,为1.42%,最高的是方案8,为2.04%。可见双臂轴支架的安装角度对船体总的粘性阻力影响较大,其主要是影响压差阻力,而对摩擦阻力基本没有影响。
图6所示为方案1外前桨双臂轴支架下游剖面的轴向速度云图,图7所示为方案1内后桨双臂轴支架下游剖面的轴向速度云图。

图6 方案1外前桨支架下游剖面轴向速度Fig.6 Axial velocity field in a plane downstream the forward propeller shaftbracketof scheme 1

图7 方案1内后桨支架下游剖面轴向速度Fig.7 Axial velocity field in a plane downstream of the aftpropeller shaftbracketof scheme 1
由图中可看出,在轴支架的阴影区内,轴向速度变化非常剧烈,轴向速度等值线成V字形分布,双臂轴支架正后方为低速区。
图8~图10所示分别为9种双臂轴支架方案在外前桨盘面典型半径Vx/V,Vr/V和Vθ/V处的周向分布,图11~图13所示分别为9种双臂轴支架方案在内后桨盘面典型半径Vx/V,Vr/V和Vθ/V处的周向分布。
图8 外前桨盘面典型半径处Vx/V的周向分布Fig.8 Circum ferentialdistribution of Vx/V on the forward propeller disk

图9 外前桨盘面典型半径处Vr/V的周向分布Fig.9 Circum ferential distribution of Vr/V on the forward propeller disk
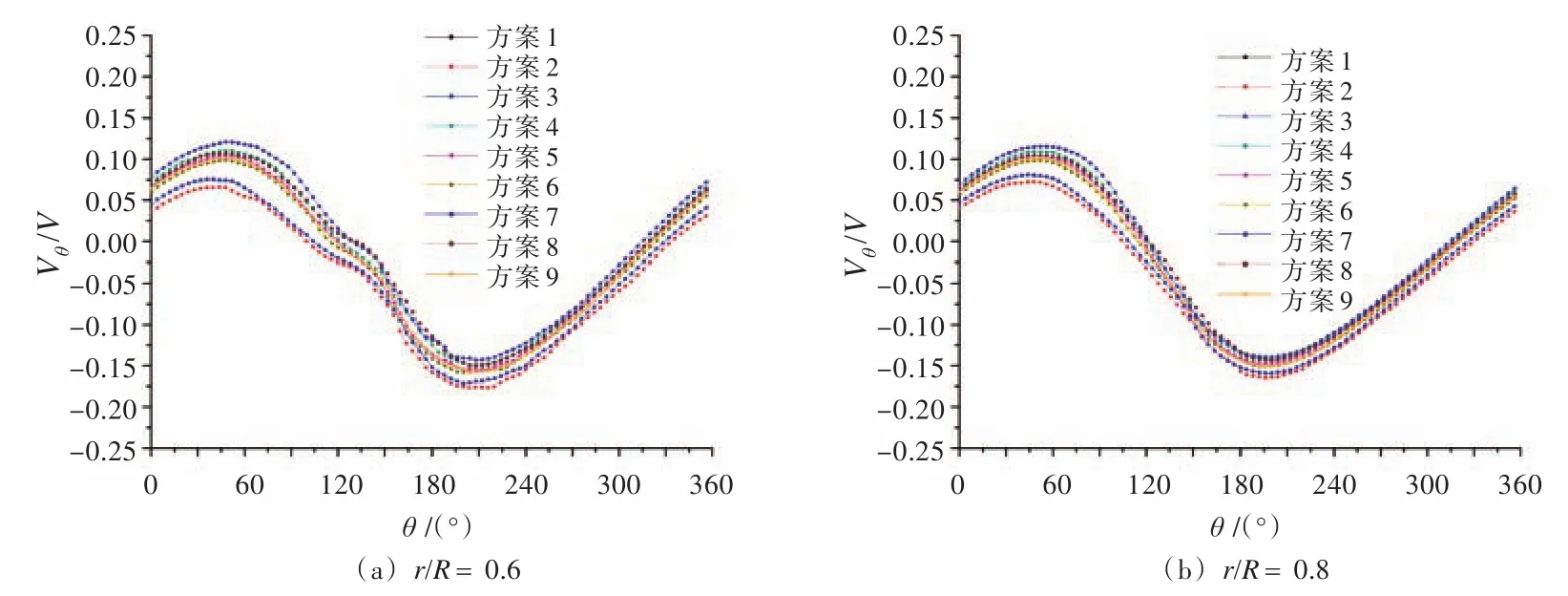
图10 外前桨盘面典型半径处Vθ/V的周向分布Fig.10 Circum ferential distribution of Vθ/V on the forward propeller disk
图11 内后桨盘面典型半径处Vx/V的周向分布Fig.11 Circum ferential distribution of Vx/V on the aftpropeller disk

图12 内后桨盘面典型半径处Vr/V的周向分布Fig.12 Circum ferential distribution of Vr/V on the aftpropeller disk
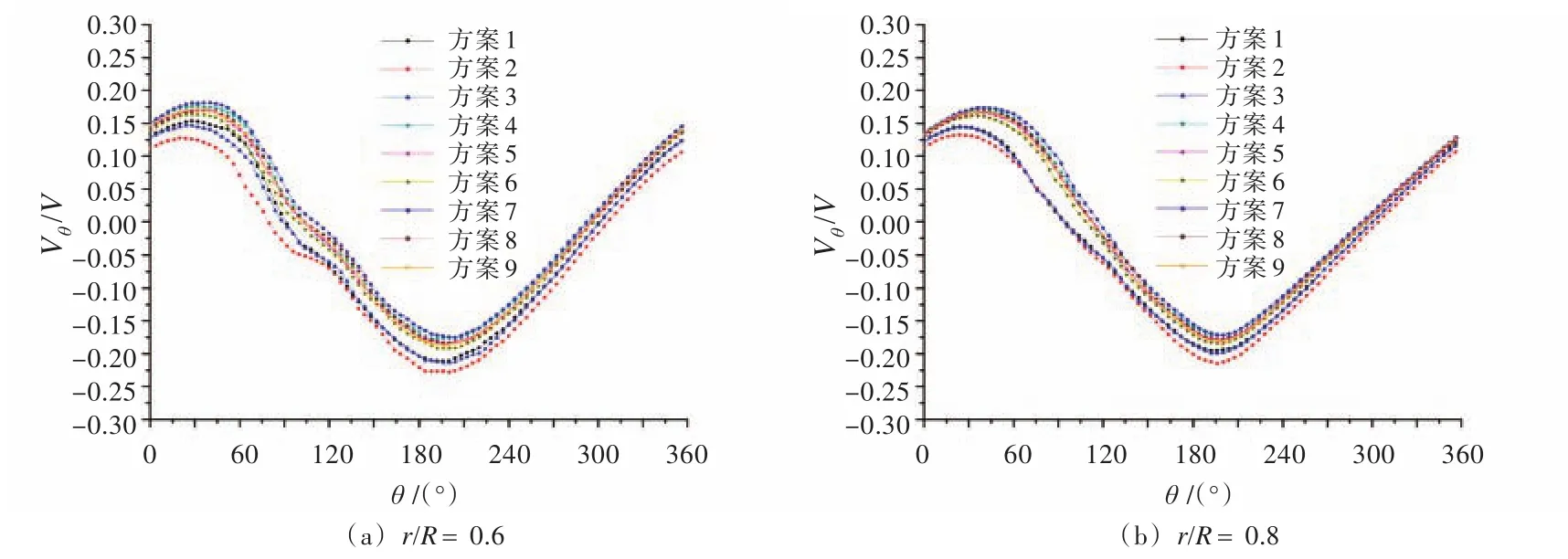
图13 外前桨盘面典型半径处Vθ/V的周向分布Fig.13 Circum ferentialdistribution of Vθ/V on the aftpropeller disk
由以上各图可看出:
1)不管是外前桨盘面还是内后桨盘面,轴向和径向速度在双臂轴支架阴影区的变化比较剧烈,产生了较严重的峰谷现象,这种峰谷的幅值随着桨盘面半径的增加逐渐减小。这表示螺旋桨在经过这些区域时性能会受到严重影响,有可能会出现严重的空泡和振动现象。
2)双臂轴支架对周向速度的影响主要在0.8R区域以内,而在0.8R以外则几乎不受影响,成比较规则的余弦分布。
3)9种双臂支架方案的三向速度变化规律基本一致。
进一步比较了这9种双臂轴支架方案的桨盘面流场的均匀程度,提出了流场不均匀度系数,定义如下:

式中,fx,fr,fθ分别指轴向、径向和周向不均匀度系数;ux(r,θ),ur(r,θ),uθ(r,θ)分别指桨盘面处的轴向、径向和周向速度;指桨盘面r半径处的轴向、径向和周向平均速度。由于周向速度的平均值在0左右,故本文不计算周向不均匀度系数,只计算0.4R~1.0R的圆环面不均匀度系数,计算结果如表3所示。
由表中可看出:
1)在同一方案中,外前桨和内后桨盘面的径向不均匀度系数比轴向不均匀度系数大;内后桨盘面的径向不均匀度系数比外前桨盘面的大。
2)不同双臂轴支架方案外前桨和内后桨盘面的轴向不均匀度系数差别较小,而径向不均匀度系数的差别则较大。

表3 各双臂轴支架方案桨盘面的轴向和径向不均匀度系数Tab.3 Axialand radialuneven coefficients on the p ropeller disk of different tw in shaft bracket schem es
这说明双臂轴支架对桨盘面径向速度的干扰较大,支架剖面形状和安装角度的变化对桨盘面轴向的伴流场影响较小。
3 结 语
本文采用RANS方法对船体带附体的三维粘性流场进行了数值模拟,重点分析了双臂轴支架的剖面形状和安装角度对船舶粘性阻力和螺旋桨盘面伴流场的影响。通过计算发现:
1)由于附体的存在,带附体的船舶螺旋桨桨盘面处的伴流场比裸船体的伴流场更加不均匀,伴流峰谷现象更严重。
2)双臂轴支架剖面形状和安装角度的改变对螺旋桨盘面轴向伴流分量的影响较小,而对径向和周向伴流分量的影响则较大。
3)双臂轴支架的剖面形状对船体的阻力影响较小,但其安装角度对船体阻力的影响却较大,因此,依据双臂轴支架前方流场速度矢量的方向来确定双臂支架的安装角度是工程上比较实用的做法。
[1]夏国泽.船舶流体力学[M].武汉:华中科技大学出版社,2003:146-147.
[2]黄胜,单铁兵.附体对船尾伴流场的影响研究[J].哈尔滨工程大学学报,2008,29(11):1147-1153.
HUANG S,SHAN T B.The effects of appendages on ship's wakes[J].Journal of Harbin Engineering University,2008,29(11):1147-1153.
[3]常煜,张志荣,赵峰.多块结构化网格在含附体水面船模粘性流场数值计算中的应用[J].船舶力学,2004,8(1):19-25.
CHANG Y,ZHANG Z R,ZHAO F.Application of multi-block structured grid to computation of viscous flow around a ship with appendage[J].Journal of Ship Mechanics,2004,8(1):19-25.
[4]BJORN R,NICOLASB.Drag and wake prediction for shipswith appendages using an overlapping grid method[C]//Proceedingsof26thSymposium on Naval Hydrodynamics.Rome,2006:121-410.
[5]毕毅,郭峰,王林,等.双尾鳍和轴支架对800t级排水船操纵性影响的模型对比试验研究[J].海军工程大学学报,2008,20(2):52-55.
BIY,GUO F,WANG L,et al.Experimental study on the effectof twin skeg and tail-shaft strutonmaneuverability ofmodel of 800 t ship[J].Journal of Naval University of Engineering,2008,20(2):52-55.
[6]王展智,肖迪,熊鹰,等.三种艉部附体方案的粘性阻力数值计算[J].海军工程大学学报,2010,22(1):45-49.
WANG Z Z,XIAO D,XIONG Y,et al.Numerical calculation of viscous resistance in three differentstern appendage cases[J].Journal of Naval University of Engineering,2010,22(1):45-49.
[7]章梓雄,董曾南.粘性流体力学[M].北京:清华大学出版社,2011.
[8]王福军.计算流体动力学分析[M].北京:清华大学出版社,2004.
[9]张兆顺,崔桂香,许春晓.湍流理论与模拟[M].北京:清华大学出版社,2005.

