支持多时隙业务的MTS-Clos网络结构及其建模分析
孙 倩 许 都
(电子科技大学宽带光纤传感与通信教育部重点实验室 成都 611731)
1 引言
随着网络业务融合、移动应用、物联网、云计算等新兴战略产业的发展,信息网络基础设施加速向宽带融合、泛在智能方向演进。IP技术作为承载网的必然选择,需要满足高带宽、多样化的数据、语音、视频等大量融合业务的传输与交换压力[1]。特别是在核心网部分,IP网络的流量和规模的膨胀发展,必然使得系统容量、端口速率等方面性能的提升成为急需解决的问题。
当交叉连接容量较大时,Clos矩阵[2,3]需要控制的交叉结点数量比平方矩阵(即Crossbar)大为减少[4]。同时,若Clos矩阵的中间级设为固定容量,则当需要扩容时仅需扩大输入级和输出级的容量即可。这在很大程度上满足了容量平滑增长的要求,因此Clos矩阵是目前交叉连接设备的主流应用矩阵。
目前对Clos网络结构的研究,主要根据构成交换网络的交换模块是否具有缓存能力而分为两类:无缓存和有缓存Clos交换结构。对于前者,典型的SSS (Space-Space-Space)Clos网络已大量应用于包交换[5,6],同时有学者提出可以将无缓存的Clos网络应用于数据中心网络[7];对于后者,在传统共享缓存MMM(Memory-Memory-Memory)Clos结构的基础上,文献[8]在近期提出了MMeM结构,以克服MMM结构下的队头阻塞[8]。此外,文献[9]从理论和仿真方面研究了SMM(Space-Memory-Memory)Clos网络在高速突发业务下的网络性能。
对于一个交换结构,其在一定网络资源或规模下的阻塞率是其交换性能的关键表征参数。针对Clos交换结构,经典的概率分析模型有Lee模型[10],Jacobaeus模型[11]和Yang模型[12],这3个模型都是用来计算在随机选路策略下三级Clos网络的阻塞概率。其中Yang模型由于考虑了级间链路复用,故此其分析结果更为精确。 此外,文献[13]利用了类似的分析方法,对Clos网络的多播阻塞率进行了深入的研究。
不同于传统的Clos网络,本文提出一种应用于多时隙业务的三级Clos网络,并对其阻塞性能进行理论和仿真研究。多时隙业务是指输入模块接收的主要是SONET/SDH或OTN的数据流,此类数据流的特点是:高等级的数字信号系列可通过将低速率等级的模块通过字节间插复用而成。同时,近期VLSI设计技术与半导体工艺水平的发展,也使得MTS-Clos(Multiple Time Slot Clos network)结构的可实现性问题得以解决,如Velio公司的VC2002芯片即可高密度地实现快速时隙交叉。针对这种多时隙多级Clos网络结构,目前尚没有较为严格的理论分析模型可供参考,这使得基于传统分析结论所进行的工程应用设计具有一定的盲目性。
本文第2节将给出基于多时隙交换的三级Clos网络结构MTS-Clos;在第3节对多时隙环境下的三级Clos网络阻塞率分析模型进行论述;第4节是数值仿真结果及分析计论;最后是结论。
2 基于TST的三级Clos结构
传统的三级对称Clos交换结构如图1所示,其中一、三级是r个n×m的交换模块,中间级是m个r×r的交换单元。根据网络的阻塞特性可将其分为3类[4],当满足m≥ 2n- 1时,是严格无阻塞网络;当满足m≥n时,是可重排无阻塞网络;第三是广义无阻塞网络。明显地,严格无阻塞条件下的网络硬件实现代价很高,这使得实际应用中可重排无阻塞网络成为首选。这类网络中业务寻径的性能主要决定于路由算法,而目前应用中的路由算法普遍存在重排次数多、重排路径长等缺点。
鉴于此,我们提出一种新的结构:即每一级不再是简单的空分结构或是共享缓存交换结构,而是由具有时分和空分功能的 TST(Time-Space-Time)构成,我们称具有n个输入、m输出端口,链路容量是t的TST的交叉规模是nt×mt。图2是4个输入端口,链路容量是4时隙的TST。图中每个字母代表一个颗粒,即 SONET/SDH中的低速信号。由于低速信号是以字节间插方式复用进高速信号的帧结构中的,这样低速信号在高速信号里的位置是固定的、有规律性,也就是有可预见性。这样就能从高速信号中直接插/分出低速信号。

图1 三级Clos网络C(n,m,r)
MTS-Clos交换网络结构C(m,n,r,t)是如下结构:输入、输出级是由r个交叉规模nt×mt的TST;中间级是m个交叉规模rt×rt的TST,如图3所示。输入级模块可将大颗粒业务拆分成小颗粒(基本颗粒),如将任意 STM-N的业务请求拆分成 STM-1请求,在网络中独立寻路,然后在输出级模块进行时隙整合,恢复为原始大颗粒业务输出。
3 多时隙环境下的阻塞率分析模型
现有的分析模型主要针对传统的不具有多时隙交叉能力的 Clos网络进行阻塞率分析,在此基础上,本节中对分析多时隙环境下MTS-Clos网络的阻塞率进行研究。
3.1 假设与符号定义
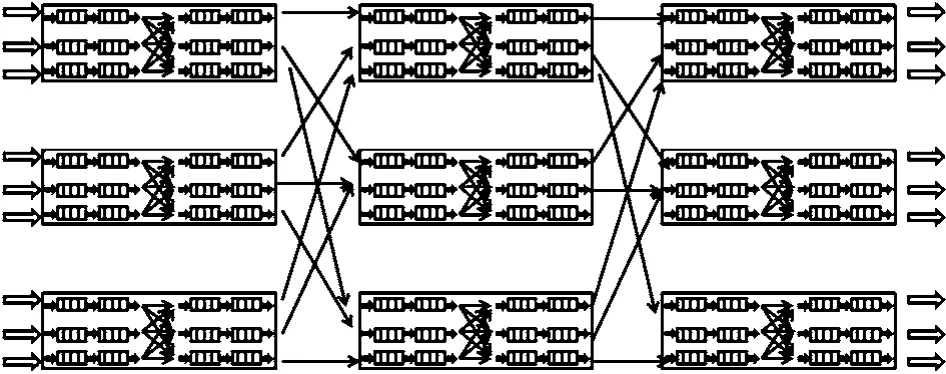
图3 由TST构成三级Clos交换网络
定义1 如图3所示网络,所有模块(输入级、中间级、输出级)都具有时隙交叉能力。设链路容量为t时隙,定义这样的网络为MTS-C(m,n,r,t)。
定义2 输入级第g个模块的输入端口定义为Ig={ig,i|i∈ { 1,…,n}},其中g∈ { 1,…,r}。输出级第h个模块的输出端口定义为Oh={oh,j|j∈ { 1,…,n}},其中h∈ { 1,…,r}。
定义3 输入级第g个模块的第i个端口到输出级第h个模块的第j个端口的请求定义为C(ig,i,oh,j)。
定义4 请求C(ig,i,oh,j)到达之前,Ig模块n1条链路忙,Oh模块n2条链路忙。设n1,n2中有k对链路共用中间级,则称为k-链路复用(k- overlapped)。
假设 1 每条链路繁忙的事件是相互独立的。当业务负荷不是很高、网络规模较大时,该假设近似成立。
假设 2 每个时隙可以被随机地分配到有空闲的中间级链路上,即负载均匀分布在所有链路上。设pslot∈[0,1]是级间链路忙的概率,qslot=1-pslot是级间链路空闲的概率。
假设 3 输入级-中间级忙的链路与中间级-输出级忙的链路,其概率分布函数服从二项式分布。
假设 4 外部输入/输出链路和内部交叉链路的容量都是t个时隙,且交叉业务的带宽需求是基本带宽单元的倍数。带宽需求β(1 ≤β≤t)个时隙的业务用β表示,定义β为交叉业务的倍数因子。假设当前共有s个业务请求,第i请求的倍数因子是βi(1 ≤i≤s)。定义α为外部链路利用率。则α=
3.2 级间链路繁忙概率分析
方法1 求取方程整数解向量的个数
这种方法物理意义明确:方程1表示B个基本时隙需求,被随机地分配在m条容量是t的链路上,其整数解向量的个数C1是B个基本时隙的选路方式。方程2表示B-t个基本时隙需求,被随机地分配在m-1条容量是t的链路上。整数解向量的个数C2是B-t个基本时隙的选路方式。综合上述两式,则某条链路忙的概率是

上述两方程可以用贪婪算法求解,但其运算量与m成指数倍关系,当m较大时,运算量大,求解困难。
方法2 母函数法
假设存在m种物品,每个物品的个数都是t,这m种物品分别为x1,x2,…,xm;重集Q1={t⋅x1,t⋅x2,…,t⋅xm}。则上述方程1解向量的个数是求重集Q1的B排列数。由于每种物品最多可以选t种,故母函数是:f(x)=(1 +x+x2+…+xt)m。
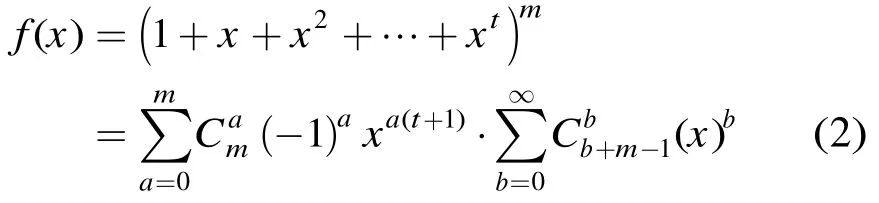
令
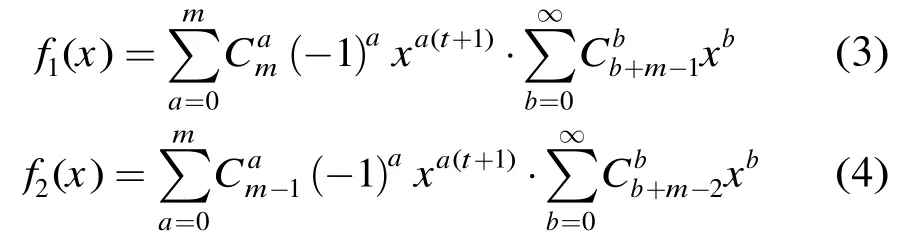
其中a,b是正整数,t表示链路容量,m表示中间级数目。求出f1(x)中xB的系数为C1,f2(x)中xB-t的系数为C2,则所要求的某个链路忙的概率是,空闲的概率:qslot=1 -pslot。
3.3 网络MTS-Clos(m,n,r,t)的阻塞率
引理1 满足假设1,2,3,4,给定事件n1,n2,在MTS-Clos(m,n,r,t)中k对链路复用的概率是
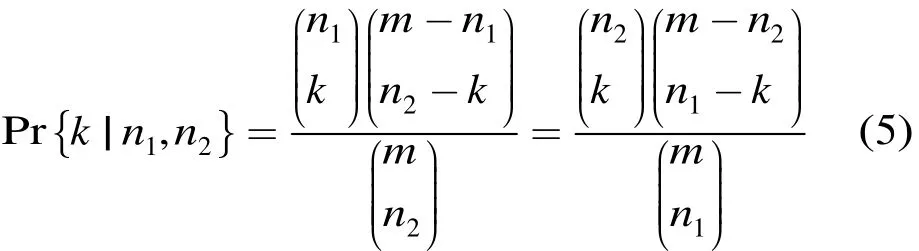
其中k是链路复用的对数。
证明 在传统Clos网络中,此引理在文献[12]已给出证明方法,实际上,在MTS-Clos(m,n,r,t)中的证明方法相同。
给定事件n1,n2,k对链路复用,则请求不被阻塞的条件是:n1+n2-k<m。注意到k的值应小于输入模块中忙的链路(n1)和输出模块中忙的链路(n2),因此:k≤min {n1,n2}。因此,给定事件n1,n2,请求C(ig,i,oh,j)不被阻塞的概率是

根据假设1,
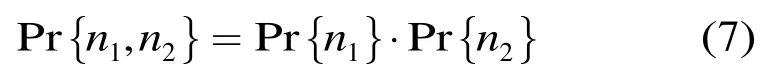
下面计算 P r{n1}和 P r{n2},由假设2,假设3在网络MTS-C(m,n,r,t)中,n1条输入级-中间级链路忙的概率是:,但由于最多由n-1条输入级-中间级链路忙,我们可得出更准确的概率:

n2条中间级-输出级链路忙的概率:
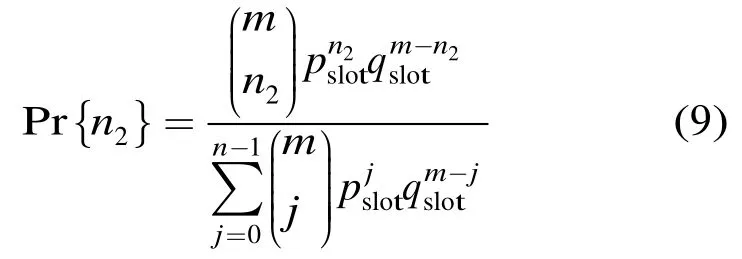
由式(6)-式(9)中,我们可以得出请求C(ig,i,oh,j)不被阻塞的概率为
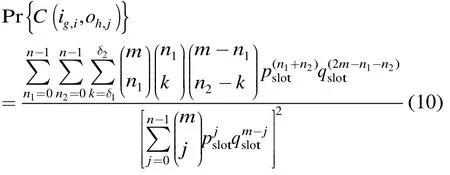
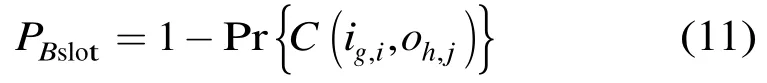
4 仿真及分析
仿真平台采用VC++编写,网络C(m,n,r,t)的所有参数均可配置,主要由业务生成模块和业务处理模块构成。业务生成模块用于生成合法业务请求,然后由业务处理模块按照随机策略分配中间级,如若不能配通,即计为一次阻塞。
Yang模型适用于基于Crossbar的空分Clos网络的分析,这类网络每一级都不具备时隙调整能力。图4是两种模型下同等配置下的Clos网络阻塞率分析结果。从图中的分析结果可以看出,基于Crossbar的空分 Clos网络的阻塞率明显高于基于 TST的Clos网络,同时三级时隙可调的 Clos网络的阻塞率比传统的线路交换网络的阻塞率下降的更快。当然这是以牺牲硬件复杂度为代价的,Yang模型所适用的是空分的Clos网络,这类网络硬件复杂度比文中所提的基于TST的Clos网络要小。
图5是网络C(m,20,20,4)的仿真结果和分析结果的对照图,链路利用率α=0.9;从图中可以看出阻塞率随着中间级规模的增大迅速下降。随着中间级规模的增大,阻塞率变小就意味着配通率的增大,重构次数的降低。分析结果稍大于仿真结果,也可以说分析模型保守地估计了网络的阻塞率;但两结果相差不大且保持着相同的趋势说明分析模块有着良好的精度。
下面考查链路容量t对阻塞率的影响。图6所示是网络C(20,20,20,t),α=0.9,阻塞率随链路容量t的变化图。图7所示是网络 C(20,21,20,t),α=0 .9,阻塞率随链路容量t的变化图。从两图都可以看出,随着链路容量的增加,阻塞率呈下降趋势。是因为随着链路容量t的增加,pslot呈下降趋势,并且当m>n时,pslot呈下降的更快,比较图6,图7,可以得出:当m>n时阻塞率随链路容量下降比m=n时更快,在我们所配置的网络中,阻塞率下降为0;即当链路利用率α=0.9,网络C(20,21,20,t)在足够大的链路容量下可以将业务全部配通。所以在构建交换网络时,如果能提供冗余的交换模块将会极大地降低重排次数。
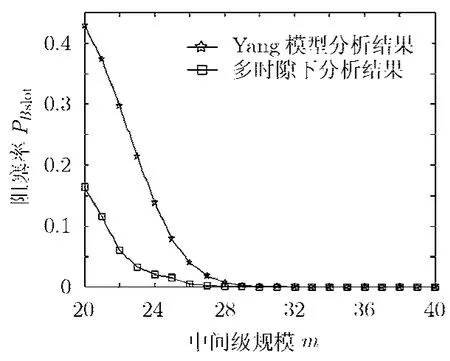
图4 两种模型下的Clos网络阻塞率分析结果
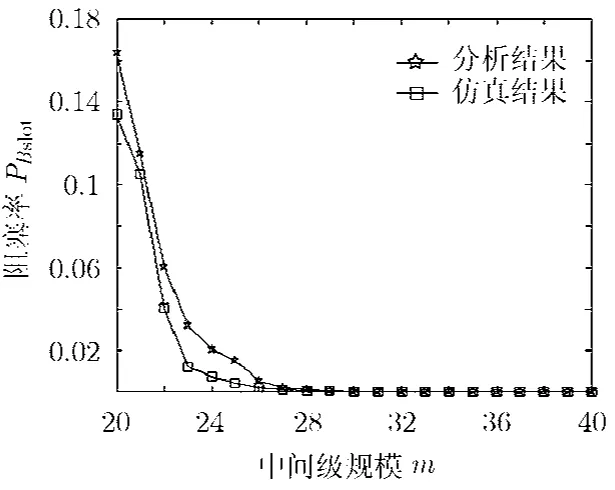
图5 网络C(m,20,20,4)的仿真与分析结果
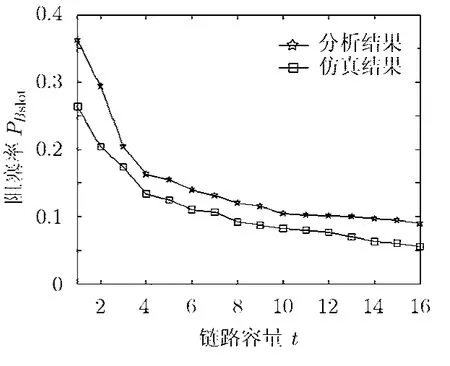
图6 网络C(20,20,20,t)阻塞率随t变化图
5 结论
本文所提出的基于TST的Clos网络,与基于Crossbar的空分 Clos网络相比虽然在构成上略为复杂,但在相同的网络规模下,基于TST的Clos网络的阻塞率更低;尤其特别的是当中间级规模m>n时,阻塞率下降得更快,当中间级规模m=n+d,d是一个很小的非负整数;配通率就可以达到100%。m=n时Clos网络是可重排无阻塞网络,但重排会引入噪声和误码;在可靠性要求很高的场合,可采用MTS-Clos结构,只需增加少量中间级就使网络无阻塞。
本文通过理论分析和仿真实验证明了 MTSClos网络的阻塞率与链路容量成负相关:输入链路容量和级间链路容量同时增加时,网络的阻塞率随之降低。该性质是基于Crossbar的Clos网络所不具备。
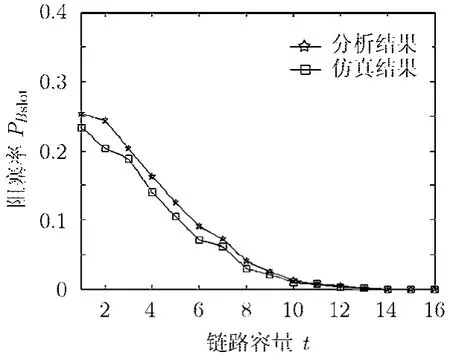
图7 网络C(20,21,20,t)阻塞率随t变化图
[1]代晓慧.对十二五期间信息通信业发展的思考[OL].www.c114.net/topic/2561/a570678.html,2010.12.
[2]Clos C.A study of non-blocking switching networks[J].The Bell System Technical Journal,1953,32(3): 406-424.
[3]Chao H J and Liu B.High Performance Switches and Routers[M].New Jersey: Wiley-IEEE Press,2007: 382-408.
[4]Benes V E.Mathematical Theory of Connecting Networks and Telephone Traffic[M].New York: Academic Press,1965:53-65.
[5]Dorren H J,Calabretta N,and Raz O.A 3-stage CLOS architecture for high-throughput optical packet switching[C].Communications and Photonics Conference and Exhibition(ACP),Shanghai,China,Nov.2-6,2009: 1-6.
[6]Oki Eiji,Kitsuwan Nattapong,and Rojas-Cessa R.Analysis of space-space-space Clos-network packet switch[C].2009 Proceedings of 18th International Conference on Computer Communications and Networks,San Francisco,CA,USA,Aug.3-6,2009: 1-6.
[7]Chao H J and Kang Xi.Bufferless optical Clos switches for data centers[C].Optical Fiber Communication Conference and Exposition (OFC/NFOEC),Los Angeles,CA,USA,March 6-10,2011: 1-3.
[8]Dong Zi-qian and Rojas-Cessa R.Non-blocking memorymemory-memory Clos-network packet switch[C].Sarnoff Symposium,Princeton,NJ,USA,2011: 1-5.
[9]Ruepp S,Rytlig A,and Manolova A V.Performance evaluation of 100 Gigabit Ethernet switches under bursty traffic[C].Optical Network Design and Modeling (ONDM),Bologna,Italy,Feb.8-10,2011: 1-6.
[10]Lee C Y.Analysis of switching networks[J].The Bell System Technical Journal,1955,34(6): 1287-1315.
[11]Jacobaeus C.A study of congestion in link system[J].Ericsson Techniques,1950,51(3): 1-68.
[12]Yang Y.An analytical model on network blocking probability[J].IEEE Communications Letters,1997,1(5):143-145.
[13]Pattavina A and Tesei G L.Modeling the blocking behavior of multicast Clos networks[C].INFOCOM 2003.Twenty-Second Annual Joint Conference of the IEEE Computer and Communications,IEEE Societies,San Francisco,CA,USA,2003,Vol.1: 756-763.

