基于圆柱共形阵的快速来波方向估计

杨 鹏 杨 峰 聂在平 李 彪 唐先发

（1.电子科技大学电子工程学院，四川 成都 611731；2.中国工程物理研究院电子工程研究所，四川 绵阳 621900）

引 言

在未来的通信和军事应用中，共形于载体表面的自适应天线阵已越来越引起人们的广泛兴趣。相对于一般天线阵，自适应共形阵有许多独特的优点，如低剖面、易伪装、灵活的波束控制和较强的抗干扰能力等［1-3］。然而，由于其结构的特殊性，共形阵也存在许多尚待解决的问题。如在进行宽角扫描时，由于载体的存在，对某些方向的来波信号，不是所有阵元都能接收到，即存在所谓的“暗区”，此时通常需要进行阵元切换，增加了系统的复杂度。当利用圆柱共形阵来进行360°来波方向估计（DOA估计）时，由于预先不知道信号的位置，一般要求所有阵元都处于工作状态，但由于仅有部分阵元能够接收到信号，从而导致信号在该阵列上的导向矢量不完整。由于天线阵元共形于载体表面，阵元的方向图无法设计为全向，即具有方向性。

目前大多数常用的高分辨率DOA估计方法，如干涉仪法［4］、多重信号分类法（MUSIC）类算法［5］、ESPRIT 类算法［6］等，都假设阵列导向矢量完整，即所有阵元都同时工作，且阵元方向图为全向。对共形阵而言，由于存在上述问题，如果直接使用此类算法进行DOA估计，往往会带来较大误差。利用基于子阵分割的 MUSIC算法［7］，可以有效克服上述问题。但由于经典的MUSIC算法是基于空间谱搜索的，较慢的速度限制了其应用。相比经典MUSIC算法，ESPRIT和Root-MUSIC算法在保证相同精度的同时可以通过求解代数方程直接得出来波方向，无需空间谱搜索，效率较高，但ESPRIT和Root-MUSIC算法对阵列的拓扑结构有特殊要求，一般只能应用于均匀直线阵上。虽然，近年来有学者提出可以应用在均匀圆阵上的基于模式空间变换的 UCA-RBMUSIC和 UCA-ESPRIT 算法［8］，但由于需要满足周期性激励条件，仍然无法应用到一般的曲线共形阵中。通过子阵分割和虚拟内插技术［9］，将ESPRIT算法和Root-MUSIC算法应用在圆柱共形阵上，实现了基于共形阵的快速DOA估计，仿真结果证实了该方法的有效性。

1.子阵分割和虚拟内插变换技术

图1所示为一圆柱共形阵，假设阵元数为M，均匀分布在圆周上，如以圆心为参考点，则第m个阵元的坐标为（r，βm），其中r为圆柱半径，βm为该阵元所在位置的方位角，βm=2（m-1）π／M，m=1，2，…，M-1，M.设有p（p＜M）个不相关的同频窄带信号从远区φi（i=1，2，…，p）方向入射到该阵列上，信号与阵列同处于x-y平面，在某一时刻t，阵列接收到的数据可以表示为

图1 16元圆柱共形阵，信号从φ＝π／2方向入射

式中:X（t）=［x1（t），x2（t），…，xM（t）］T是整个阵列接收的数据向量；F=［f（φ1），f（φ2），…，f（φp）］为阵列方向图矩阵，其中f（φi）=［f（φi-β1），f（φi-β2），…，f（φi-βM）］T，f（φ）为单个阵元的方向图；S（t）为表征各个来波信号的复振幅矢量；N（t）=［n1（t），n2（t），…，nM（t）］T为加性白噪声矢量；A=［a（φ1），a（φ2），…，a（φp）］为阵列流型矩阵，a（φi）（i=1，2，…，p）为第i个信号的导向矢量，a（φi）=［ejkrcos（φi-β1），ejkrcos（φi-β2），…，ejkrcos（φi-βM）］T，其中波数k=2π／λ，λ为信号波长。

假设有一窄带信号由φ=π／2入射到如上所述阵元均匀分布的M（M=16）元圆柱共形阵上，由于圆柱载体的遮挡，只有1～9号阵元能接收到该信号，此信号在阵列上的导向矢量可以表示为

可见，金属柱体的遮挡导致其余阵元接收不到信号，导致该信号的导向矢量不完整（其中的0元素）。此外，由于阵元存在方向性，各个天线对信号的响应不同，其中5号阵元由于最大辐射方向正好在φ=π／2，响应最强，而1号和9号则最弱。采取子阵分割的方法可以有效克服上述问题。

为了保持阵列导向矢量的完整性，可将阵列按每π／2一组划分为若干子阵，1～5号阵元组成子阵一，3～7号阵元组成子阵二，依次类推。16个阵元共划分为八个相同的圆弧阵，每个圆弧阵由5个阵元组成，这样可以保证对任意角度的入射信号，总有一个子阵，其所有阵元都能接收到该信号。

由于基于代数求解的快速算法（ESPRIT和Root-MUSIC算法等）不能直接应用于圆弧阵上，故可以考虑将这八个四分之一圆的弧形子阵应用内插技术变换成八个虚拟均匀直线阵。内插变换的基本思想是将空间观察区域进行划分，假设信号位于区域Φ内，将区域Φ均分为

式中:φ1，φ2为该区域的左右边界；Δφ为步长，则真实阵列的导向矢量经过内插后变为

由于是共形阵，因此这里考虑了有向阵元。在同一区域中，若存在另一个阵元为全向的虚拟阵列，其内插后的阵列导向矢量为

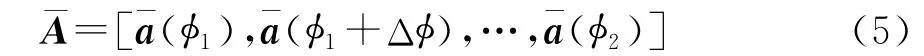
期望找到一个变换矩阵B，满足

当然，不可能找到一个理想的B满足上述关系。但可以通过优化下式

来确定最佳变换矩阵B，式中‖·‖表示求Frobenius范数，（·）H表示共轭转置。如果该比值τ小于某一门限（如10-3），则接受该变换，否则可将观察区域进一步细分，或者调整虚拟阵列几何结构，直到满足该条件为止。虚拟变换虽然运算量大，但这是一个离线过程，可预先计算好并储存在系统中。

为了精确地求得变换矩阵，需要注意三点:首先内插角度步长不可取的太稀疏，一般应小于0.1度，较小的步长会导致内插过程运算量加大，但由于内插变换是一个预处理过程，不必实时计算，故步长应当尽量取小一些。二是虚拟阵列不能和真实阵列相差太大，在选取虚拟阵列时，应当尽量使虚拟阵列在位置和拓扑结构上接近真实阵列，可使变换误差最小。图2所示为待变换的真实圆弧阵和期望通过变换得到的虚拟均匀直线阵。

图2 真实阵列和虚拟阵列

将三个真实的子阵通过内插，变换为三个虚拟的均匀直线阵。通过优化虚拟阵列的阵元间距d和阵列到原点的距离h来使得变换误差τ最小。当取内插间隔Δφ=0.1，d=0.52λ，h=0.8λ时，τ约为8×10-4，可以接受该变换。第三是变换区域不能选择太大，图3所示为当d和h取上述最优值时变换区域的大小与变换误差的关系，可见，当观测区域大于60°时，误差迅速上升，一般最大变换区域不应超过60°.对如图1所示的圆柱共形阵，可以选取每个子阵的内插区域为阵列法线方向±π／8，即子阵一（1～5号阵元）的内插区域为［π／8，3π／8］，子阵二（3～7号阵元）的内插区域为，依次类推。360°方位角共可分为八个均匀的内插区间，八个内插区间也是八个虚拟阵列的DOA估计区间。对于均匀直线阵来说，阵列法线方向±π／8是最佳测量区间。

图3 变换区域和变换误差的关系

经过上述子阵分割和虚拟变换后，真实阵列的数据协方差矩阵为［10］

式中:=XXH／K，K 为快拍数；=F·A；为信号的自协方差矩阵；σ2I为白噪声功率，则虚拟阵列的协方差矩阵为

由于BHB≠I，故应对式（9）进行预白化，即变换矩阵变为

此时有TTH=I.圆柱共形阵的数据协方差矩阵就变换为了虚拟均匀直线阵的协方差矩阵。经过这样处理后，所有可以应用在均匀直线阵上的DOA估计算法都可以应用在共形阵上。为了证明该方法的通用性，采用了ESPRIT算法和Root-MUSIC算法进行检验。

2.仿真算例

对图1所示16元均匀圆柱共形阵，圆柱半径r=λ／（4πM），阵元的极化方向为圆柱轴向（即z轴方向）。假设有两个与阵列共面（x-y），极化方向相同，且不相关的同频窄带信号分别从φ=40°和φ=90°方向入射到阵列上，快拍数为128，噪声为0均值、方差为1的高斯白噪声，其它参数采用前述的优化结果。为了简化计算，仅对1～9号阵元进行变换，独立实验100次。在仿真过程中，不失一般性，假设阵元方向图具有cosφ的形状，即第m个阵元对φi方向入射信号的响应为cos（φi-βm）.

图4和图5为两信号分别在子阵一和子阵二上使用两种算法估计出的角度和真实入射角的均方差随SNR的变化关系。从图中可以看出，对入射信号1（φ=40°），因为处在子阵一的观测区域［π／8，3π／8］内，故子阵一对该信号的估计性能要好一些。子阵二的估计信能较差，是因为子阵二中的7号阵元接收不到该信号，导致信号1在子阵二上导向矢量不完整。两种算法的性能基本相当，当SNR＞5dB时，能保证估计误差在1°以内。同理，对信号2（φ=90°），子阵二的估计性能较好，是因为该信号处于子阵二的法线方向，且位于阵元5的最大辐射方向上。当SNR＞0dB时，两种算法的估计误差均不超过1°.虽然信号2在子阵一的观测区域外，但由于在子阵一上导向矢量是完整的（因为1～5号阵元均能接收到），因此，子阵一对信号2的估计性能要优于子阵二对信号1的估计性能。由仿真结果和以上讨论得知，对信号1，接受子阵一的估计结果，对信号2，接受子阵二的估计结果。同时，ESPRIT算法和Root-MUSIC算法均获得了大致相同的估计精度，证明了该方法的通用性。

3.结 论

给出了一种在共形阵上进行DOA估计的快速而准确的方法。该方法利用子阵分割和虚拟内插变换，将圆柱共形阵变换为若干虚拟直线阵，利用ESPRIT算法和Root-MUSIC算法获得较高的估计精度和速度。此方法克服了共形阵在DOA估计中由于载体遮挡造成的信号导向矢量不完整以及阵元方向图指向不一致带来的问题，并容易推广到一般结构的曲线或曲面共形阵上，具有普适性和较强的应用价值。

［1］JOSEFSSON L，PATRIK P.Conformal Array Antenna Theory and Design［M］.New York:John Wiley and Sons，2006.

［2］TUNCER E，FRIEDLANDER B.Classical and Modern Direction of Arrival Estimation［M］.Burlington:Elsevier，2009.

［3］张福顺，焦永昌，马金平，等.弹体上S波段微带共形天线阵［J］.电波科学学报，1998，13（2）:209-212.ZHANG Fushun，JIAO Yongchang，MA Jinping，et al.Microstrip array conformal to bomb shell on S-band［J］.Chinese Journal of Radio Science，1998，13（2）:209-212.（in Chinese）

［4］何子远，王自力，龚耀寰.利用干涉原理估计相干信号DOA的新方法［J］.电波科学学报，2003，18（5）:583-586.HE Ziyuan，WANG Zili，GONG Yaohuan.A new method of estimating DOA of coherent signals by interference principle［J］.Chinese Journal of Radio Science，2003，18（5）:583-586.（in Chinese）

［5］SCHMIT R O.Multiple emitter location and signal parameter estimation［J］.IEEE Trans Antennas Propag，1986，34（3）:276-280.

［6］ROY R，KAILATH T.ESPRIT-estimation of signal parameters via rotational invariance techniques［J］.IEEE Trans Acoust，Speech，Signal Process，1989，37（7）:984-995.

［7］杨 鹏，杨 峰，聂在平，等.MUSIC算法在圆柱共形天线阵DOA估计中的应用研究［J］.电波科学学报，2008，23（2）:288-291.YANG Peng YANG Feng NIE Zaiping，et al.DOA estimation of cylindrical conformal array by MUSIC algorithm［J］.Chinese Journal of Radio Science，2008，23（2）:288-291.（in Chinese）

［8］MATHEWS C P，ZOLTOWSKI M D.Eigen structure techniques for 2Dangle estimation with uniform circular arrays［J］.IEEE Trans Signal Processing，1994，42（9）:2395-2407.

［9］FRIEDLANDER B.Direction finding with an interpolated array［C］／／In Proc，ICASSP.Albuquerque，NM，April，1990:2951-2954.

［10］王永良，陈辉，彭应宁，等.空间谱估计理论和算法［M］.北京:清华大学出版社，2004.