利用等效孔隙度法估算火成岩储层渗透率

李玮，张超谟，2，吴一雄，谢冰

（1.长江大学地球物理与石油资源学院，湖北 荆州 434023；2.油气资源与勘探技术教育部重点实验室，长江大学，湖北 荆州 434023）

0 引 言

火成岩储层由于其岩性复杂，孔、洞、缝发育，非均质性强，小柱岩样岩心常规物性分析渗透率低（仅代表其基质部分渗透率），利用常规测井处理解释方法难以准确计算其渗透率。斯通利波是井内流体与井壁地层间传播的一种流体导波，在低频时会变成管波模式，在井眼中传播时遇到孔、洞、缝会发生时差延迟，因此可以利用斯通利波信息估算地层渗透率[1－3]。目前常用的斯通利波合成反演方法需要知道处理井段内至少1个已知点的渗透率参考值以确定流体参数，在该参考值未知情况下往往误差较大，且该方法处理流程较为繁琐。笔者结合前人提出的S－Se法[4]和等效孔隙法，针对火成岩孔隙结构复杂且非均质性强的特点，提出以流体移动指数Qfm为标准建立等效孔隙评价火成岩渗透率的新方法，即建立流体移动指数与等效孔隙的关系，再通过分类建立等效孔隙与渗透率之间的关系评价火成岩渗透率值。在JL油田B区域的应用结果表明，该方法得到的储层渗透率值符合精度要求，且无需知道参考渗透率值，应用更为便利。

1 求取流体移动指数Qfm

低频情况下斯通利波变为管波模式，沿井中流体作活塞状压缩传播。当井眼穿过渗透区域或渗透缝时，会在井眼与地层之间出现一些流体运动，导致斯通利波能量损失衰减，同时导致传播速度减慢。

实测斯通利波（由阵列声波测井仪测得）受到地层渗透性的影响，及地层弹性、井径变化、泥饼和各向异性等与渗透率无关因素的影响。因此，可以将斯通利波时差分为2个部分，即无渗透性的致密层理论斯通利波时差Se与因地层渗透率存在而对应的那部分时差Sp。

如果井壁存在渗透性通道，则径向位移就包含2个部分，一部分为井壁弹性位移；另一部分为井内流体流入与井壁相交的孔隙中的部分。S－Se法就是通过计算出完全弹性非渗透地层斯通利波时差Se，然后将实测斯通利波时差S与Se进行比较，其差值反映了渗透性的影响，称为流体移动指数Qfm，Qfm能够指示地层渗流能力。计算Qfm的方法可概括为

式中，G为地层剪切模量；Kf为泥浆体积模量；K为地层渗透率，mD＊非法定计量单位，1mD＝9.87×10－4μm2，下同；ρf为泥浆密度，g／cm3；ρ为地层密度，g／cm3；Δts和 Δtf分别为地层横波和泥浆时差，μs／ft＊＊非法定计量单位，1ft＝12in＝0.3048m，下同；S 为实测的斯通利波时差，μs／ft；Se为理论弹性地层斯通利波时差，μs／ft[5]。

2 等效孔隙理论

火成岩储层可以用裂缝－孔隙双重介质岩石模型分析，其基质孔隙和裂缝两者同时都有储集和渗透作用，裂缝－孔隙岩石的渗透率等于基质渗透率与裂缝渗透率之和[3]。此时直接应用岩心数据进行孔渗分析，由于强非均质性的影响，其相关性往往很差。

所谓等效孔隙度法就是将孔隙空间，无论裂缝或是基质，无论孔隙的大小类型等因素如何，若它们引起的Qfm相同，即地层渗流能力相同，那么就认为2种介质的孔隙是等效的，视为同一种孔隙。等效后的孔隙空间总渗透率仍为岩石总渗透率，单位孔隙对应的渗透率大小即为该孔隙的平均渗透率大小＝K／φeq＝K／φt。该量减小了孔隙非均质性的影响，主要受到孔隙形状和大小的影响。

3 利用流体移动指数Qfm求取等效孔隙

图1为岩心分析孔隙度（表示等效孔隙度）与流体移动指数关系，裂缝可等效为Qfm（渗流能力）相同的较大基质孔隙，故加入孔喉结构较理想的大孔隙岩心数据表征裂缝性孔隙与流体移动指数关系。拟合出公式并将英尺单位化为米制单位得

式中，φeq为等效孔隙度，%；φ岩心分析孔隙度，%；Qfm为流体移动指数，μs／m。

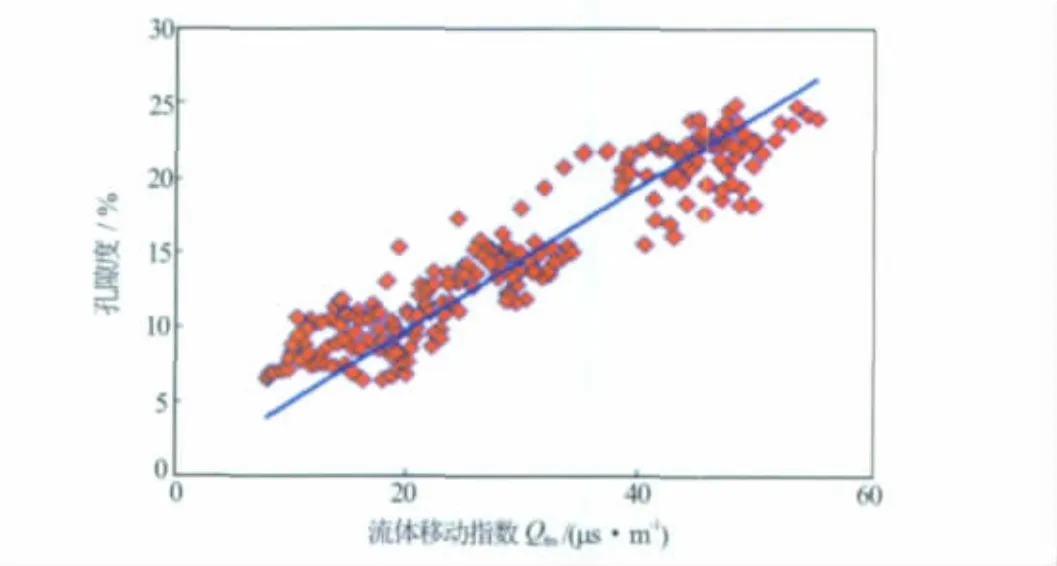
图1 B地区流动指数与全岩心有效孔隙度关系

4 分类建立渗透率评价模型

图2为深浅电阻率之比与渗透率交会图，横轴为100倍渗透率值，mD；纵轴为深浅电阻率比值。红色数据点表示m＞0.27，蓝色数据点表示m≤0.27。从图2中可以得知深浅电阻率比值不能直接用于计算渗透率值，但可以用于对渗透率值进行分类。由Fisher线性判别法[3]可得到其分界线方程

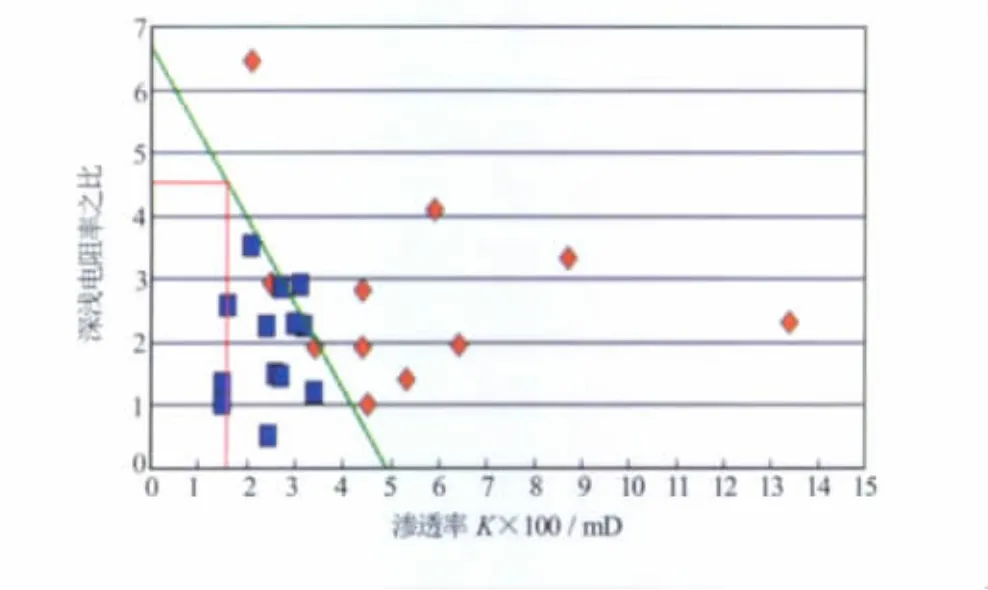
图2 数据交会分类方法

应用最小错误率贝叶斯决策判别。经分析该地区渗透率满足正态分布条件，利用已知数据点可得到其渗透率的概率密度函数。渗透率为K×102，mD。

对应于每个深度点，由于其深浅电阻率比值Rt／Rxo已知，故可由分界线方程（5）求出分界点K0值（见图2中红线），将该分界点带入渗透率的概率密度函数公式中，则可计算得到K值落在孔隙形状较易渗流部分的概率P1和K值落在较难渗流部分的概率P2。P1、P2计算公式为

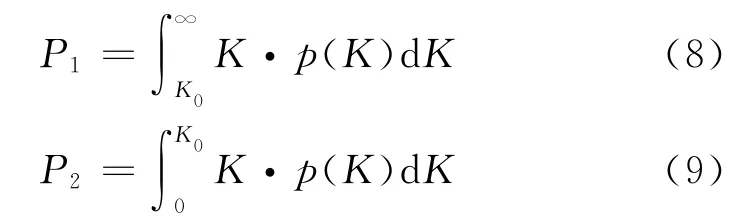
图3为分别拟合2类数据点等效孔隙与平均渗透率之间关系，红色岩心数据为m＞0.27数据点，黄色岩心数据为m≤0.27数据点，各类岩心数据相关系数较好。将式（4）代入图3拟合公式中得如下2类点对应的渗透率计算公式

m＞0.27时，计算公式为

图3 B区全岩心等效孔隙与平均渗透率分类关系

m≤0.27时，计算公式为

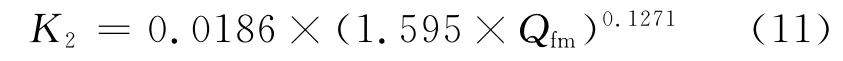
式中，K1、K2分别为较易渗流与较难渗流2类对应的渗透率，mD。

5 应用实例

图4为B区域C1井非裂缝段评价结果。第4道为岩心分析孔隙度φ和等效孔隙度φeq，可见在非裂缝段等效孔隙度值与岩心孔隙度值具有较好的对应性。第5道为计算渗透率值Kc和岩心分析渗透率K对比结果，可见非裂缝段渗透率计算结果是有效的。

图4 C1井非裂缝段渗透率剖面

图5为B区域C2井裂缝段渗透率评价结果。图5中4186～4204m段以裂缝性孔隙为主，可见第4道等效后孔隙度φeq为25%；第5道中蓝线K为文中方法计算渗透率值，红线Ks为斯通利波反演方法得到的渗透率，2种方法得到的结果相近，说明文中方法在裂缝段也是有效的。

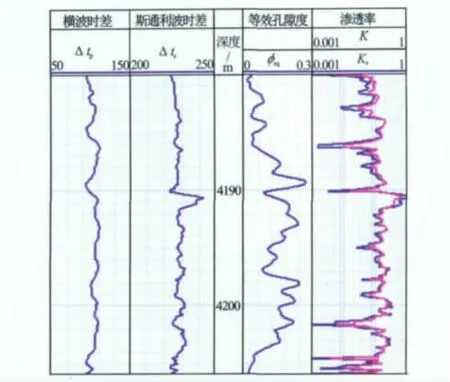
图5 C2井裂缝段渗透率剖面

6 结 论

B区域火成岩储层岩性及孔隙空间结构复杂、非均质性强、裂缝大量发育，致使常规测井方法难以准确计算火成岩储层渗透率。提出由斯通利波时差求取流体移动指数Qfm，并由此定量等效孔隙度大小，再由岩心数据分类建立等效孔隙度与等效孔隙度下平均渗透率间关系，用以估算火成岩渗透率的新方法，从而避免了斯通利波合成反演方法中较大的计算量，且无需每口井的参考渗透率值。在JL油气田B区域储层评价中取得了较好的应用效果，证实了文中方法的有效性。

[1]唐晓明.定量声学测井[M].北京：石油工业出版社，2004.

[2]杨胜来，巍俊之.油层物理学[M].北京：石油工业出版社，2009，154-156.

[3]边肇祺，张学工.模式识别[M].北京：清华大学出版社，2010，93-95.

[4]Hornby.Method for Determing Formation Permeability by Comparing Measured Tube Waves with Formation and Borehole Parameters：US Patent，4797859[P].

[5]Canady W，Spooner P.Permeabilty Estimation from Stoneley Amplitude，Corrected for Borehole Geometry and Rugosity[C]∥SPE，96598.

[6]Brie A，Endo T.Quantitative Formation Permeability Evaluation from Stoneley Waves[J].SPE Reservoir Eval.＆ Eng.，April 2000（2）：109-117.

[7]Paillet F L，Cheng C H，Tang X M.Theoretical Models Relating Acoustic Tube Wave Attenuation To Fracture Permeability-Reconciling Model Results with Field Data[C]∥ SPWLA 30th Annual Logging Symposium，June 1989：11-14.

[8]Endo T，et al.Fracture and Permeability Evaluation in a Fault Zone from Sonic Waveform Data[C]∥SPWLA 38th Annual Logging Symposium，15-18June，1997.