极区电离层加热能量吸收率的非相干散射测量
徐 彬 王占阁 程木松 许正文 吴 健 吴 军 薛 昆
(1.中国电波传播研究所,电波环境特性及模化技术重点实验室,山东 青岛 266107;2.中国科学院空间天气学国家重点实验室,北京 100190;3.西安电子科技大学理学院,陕西 西安 710071)
引 言
加热效应的大尺度仿真通常使用欧姆加热理论来解释。欧姆加热理论可以实现从D层到F层上千千米的电离层加热效应的数值模拟。1978年,Gurevich基于一组流体力学方程提出了电离层加热的基本理论[1]。在低电离层,仿真使用连续性方程和能量方程,连续性方程主要考虑与温度存在依赖关系的复合率,能量方程则主要考虑由介电常数虚部引起的电波吸收能流和碰撞引起的能量损失[2-4]。电离层中电子能量的损失机制十分复杂,主要损失机制包括电子与正离子的弹性碰撞、电子和中性离子的弹性碰撞、旋转和振动能级的激发以及原子氧电子能级和精细结构的激发等[5-8]。在高电离层,中性粒子浓度下降,碰撞效应减弱,热传导、扩散和漂移等输运过程起主要作用。因此,仿真的连续性方程和能量方程中须考虑输运项的影响,为此,就必须引入动量方程[9-12]。尽管当前的数值仿真方程已经充分考虑了F层的输运过程,但高电离层仿真中,还存在一个严重的缺陷,即对反射点处电波能量吸收率的精确描述。
现有的电波能量吸收率模型中,低电离层的欧姆加热理论模型考虑了碰撞吸收和电波传播过程,对加热过程给出了相对较为准确的描述[3-4,13]。尽管如此,该模型通常过高估计了加热效应,实测结果通常观测不到该理论模型所预测的加热特征[13]。对高电离层来说,基于欠密加热的欧姆加热理论模型[14],尽管模型较为严谨,但实际高电离层加热试验过程中,我们更关心过密加热的加热特征,而该模型不能描述反射高度处显著的加热特征。修正的电波能量吸收率模型中[15],在欧姆吸收项前引入一个经验系数,用于表征参量不稳定性、磁旋谐振和上混杂谐振等异常吸收效应。然而事实上,欧姆吸收与其他吸收机制应属并列关系,电子温度变化引起的欧姆吸收的改变并不应以乘积的方式反映到能量吸收项上,这在物理原理上即存在严重的缺陷。
尽管反射高度的电波能量吸收机制十分复杂,电波能量吸收率的理论计算难以实现,然而可以通过非相干散射雷达的实测结果,对电波吸收通量进行推算。2009年9月我国在挪威开展了电离层加热的二维特征诊断试验,本文利用欧洲非相干散射雷达的实测数据,结合稳态的能量吸收方程和动量方程,计算了反射高度附近的电波能量吸收通量,在此基础上讨论了吸收通量的统计特征。
1.理论方法与计算模型
电离层加热条件下,电离层中电子满足动量和能量守恒方程[10-12,15]
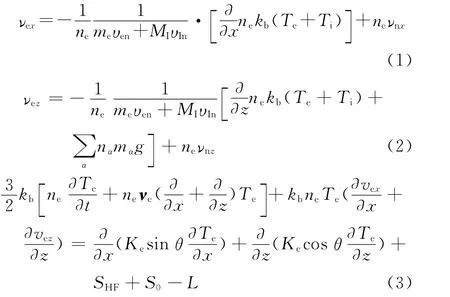
式中:vex和vez分别为水平方向和垂向的电子漂移速度;ve为电子速度矢量;νnx和νnz分别为水平方向和垂向的中性粒子漂移速度;ne和nα电子密度和α粒子的密度;me和mα为电子和α粒子的质量;MI为等效离子质量;g为重力加速度;υIn和υen分别为离子和电子与中性粒子的碰撞频率;kb为玻尔兹曼常量;Te和Ti为电子和离子温度;Ke为热传导系数;θ为热传导方向和垂向夹角;SHF为电波能量吸收率;S0为太阳能量吸收率;L为能量损失率。则对加热前时刻,电子速度满足

式中:νex0、νez0、ne0、Te0和 Ti0分别为加热前的电子速度、电子密度、电子温度和离子温度。加热前高频(HF)电波吸收通量为零,因此,可计算出太阳引起的能量吸收为
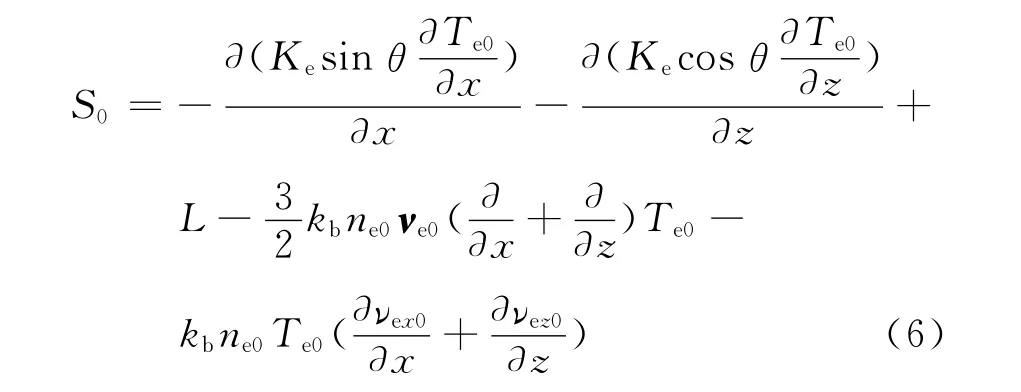
加热后的电子速度为

将上述两式带入式(3)可得

联立式(4)~(9),代入非相干散射雷达的实测结果,即可使用式(9)计算出电波能量吸收率的数值结果。
2.非相干散射雷达测量结果
2009年8月,我国在挪威开展了电离层加热二维特征试验研究[16]。由于电离层临频较低,为保证过密加热,加热天线采用了阵列2.加热频率在4.04~4.544MHz之间变更,依据电离层状态进行调整。加热循环为8分钟开,4分钟关,加热波束方向指向地磁场方向。加热效应观测主要利用超高频(UHF)非相干散射雷达,实验模式采用beata工作模式。为保证诊断设备与加热天线指向相匹配,拟写了UHF雷达扫描模式scan_cn4,使得在加热波束方向变化时,诊断雷达的扫描扇区做相应调整。
电波能量吸收率计算所需要的电离层参量中,非相干散射雷达可以直接探测的有三个,即电子温度、电子密度和离子温度。因此,对8月16日~8月19日期间40起加热事件加热前后的电子温度、电子密度、离子温度,以及仰角和高度信息进行了提取。为得到电波能量吸收率的细致结构,我们对提取后的结果进行了二维插值,使其空间分辨率提高至2km.除这三个电离层参量外,其余电离层参数和中性大气参数由模型给出,其中氧原子、氧气分子、氮气分子浓度和中性气体温度由中性大气模式MSIS95给出[17],NO+、O+2和O+浓度由国际参考电离层模型IRI2007给出[18]。时间取40起加热事件的起始时刻,空间分辨率同样取2km,并假设这些背景参数水平均匀分层,故可直接将一维数据扩展至二维。图1(见422页)给出了40起加热事件电波能量吸收率的计算结果。从图1可以看到:除16日的Case3、18日的Case5和19日的Case2,其余加热时刻均可得到显著的电波能量吸收结构。能量吸收基本呈近高斯分布,但结构在横向和纵向上并不沿能量吸收中心对称。尽管以前的研究结果表明磁天顶的能量吸收最为显著[19],但从试验观测结果来看,能量吸收中心并非全部位于场向,而是散布在场向周围。从分布形态来看,与预测的结果不同,能量吸收率的结构并不大都沿场向分布,除16日Case1、17日Case1、Case3、Case4和18日Case3外,其余时刻能量吸收结构基本沿水平轴和垂直轴对称。
温度探测中,16日和17日与18日和19日(包括17日Case7、Case8)呈现出完全不同的形态特征,一类温度增强结构处在150~200km之间,横向尺度约为50km,温度增强的绝对值不大,但相对增幅明显;另一类温度增强结构处在峰值高度附近,横向尺度特征与第一类温度增强类似,但纵向尺度更大,且温度增强的绝对值很大。尽管如此,18日和19日的电波能量吸收率计算结果并未呈现出显著的大范围分布结构,而是与16日和17日的分布结构较为类似,均为近高斯分布。温度增强与能量吸收的分布形态不同,这主要是因为在峰值高度附近,吸收的电子能量沿磁力线向上下两侧传递,峰上电子密度、离子密度减小,中性粒子密度也按指数衰减,电子的自由程更大,这使得能量可以传递到更远的位置。向下传递时,尽管电子密度、离子密度也在减小,但中性粒子密度迅速增加,电子能量损失得很快,因此,温度增强结构的空间尺度不大。当反射高度远离峰值高度时,能量向下传递的机制与上述过程相同,而向上传递时,尽管中性粒子密度也按指数衰减,电子密度、离子密度却在增加,这同样使得能量损失率随高度增加而增大,温度增强结构的空间尺度维持在很有限的空间范围内。我们同样计算了电波能量的损失率,能量吸收率与损失率相比,形态特征较为类似,但损失率弥散的范围更广,而吸收凝缩在中心附近,随距中心位置渐远,吸收率迅速衰减至零。这主要是因为能量吸收主要发生在反射高度和不稳定性发生高度上,而损失则发生在所有温度增加区域,加热会使电子扩散至更大的范围,因此,损失率的空间尺度更大。从能量吸收率幅度的对比来看,16日和17日的能量吸收率要比18日和19日的小一个量级,这主要是因为18日和19日是由多种不稳定性被激发而引起的。
前面给出了电波能量吸收率理论模型和非相干散射雷达的观测结果,这里对电波能量吸收率的统计特性进行进一步的分析。图2给出了电波能量吸收率最大值方向和地磁场方向的关系。由图2可见,能量吸收中心基本均匀地分布在场向两侧,其均值为78°,仅略大于地磁场方向,标准差为1.7°.对比16日、17日和18日、19日的结果可以看到,16日、17日吸收中心分布较为分散,且分布在场向两侧,而18日、19日吸收中心离场向更为接近,但多分布在场向以上。这意味着我们进行泵波频率接近临界频率的电离层加热试验时,加热扰动区域的分布更为稳定。
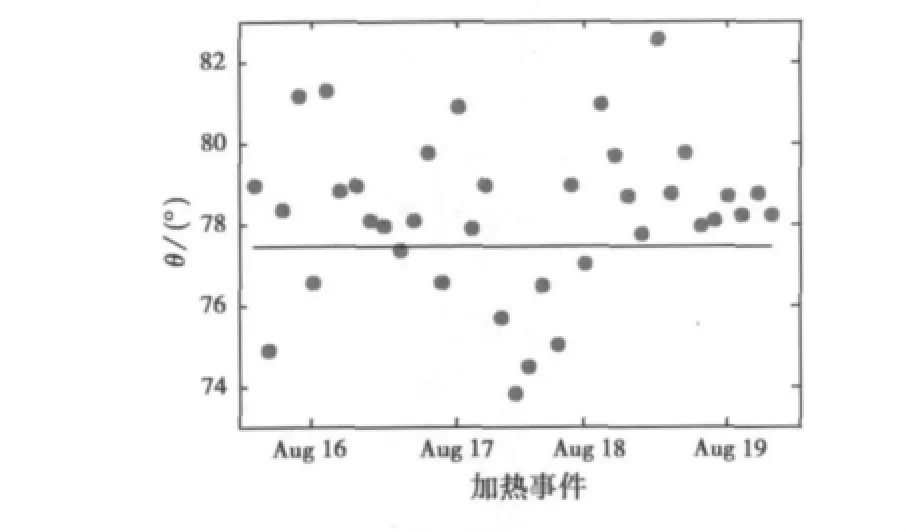
图2 电波能量吸收率最大值方向(点)和地磁场方向(实线)关系图
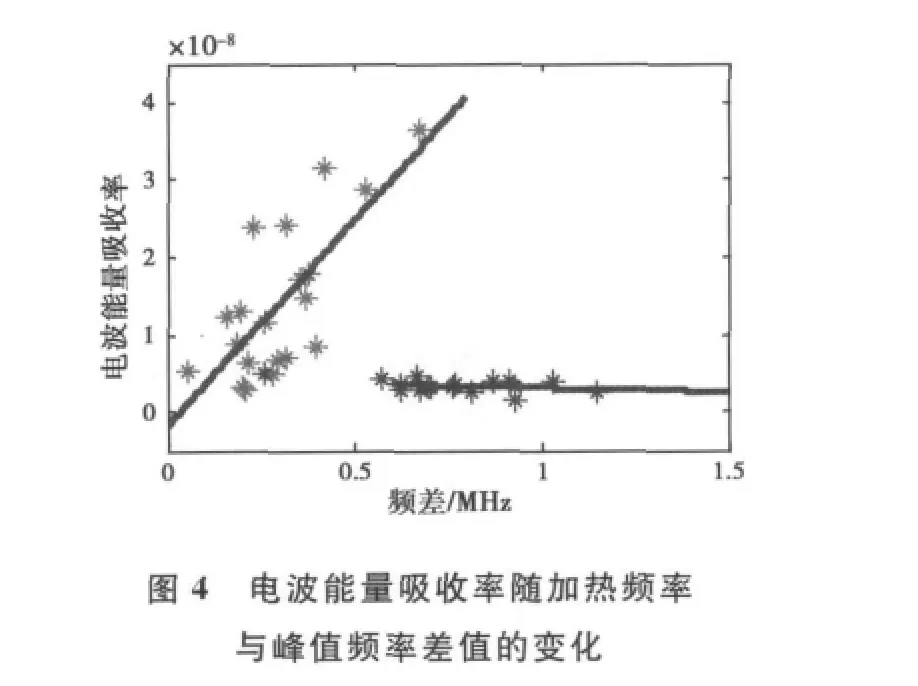
图3给出了电波能量吸收率最大值高度和反射高度的关系,从图3可以看到:16日、17日和18日、19日的高度关系明显不同,16日、17日能量吸收中心高度多位于反射高度以下10km附近,这意味着16日、17日的加热实验中能量的吸收并不是纯增长模式(电离子体与HF加热电波的本征谐振)在起主要作用,而是发生在反射高度以下的某一不稳定性主导了能量的吸收。而18日、19日能量吸收中心高度位于或略高于反射高度,这意味着能量的吸收中纯增长模式和靠近反射高度附近的不稳定性在起主要作用,从电离层变态的效果来看,后者的能量吸收更为充分。16日、17日和18日、19日的高度关系的显著差异也证明了两种类型加热效应的加热机制并不相同。图4给出了电波能量吸收率最大值随加热频率与峰值频率之差的变化。从图4可以看到,电波能量吸收率随频差的增加线形增加,在0.6 MHz附近存在突跳,吸收率最大值从3.6×10-8锐减至4.1×10-9,在此之后,随频差增大电波能量吸收率缓慢下降。

3.结 论
人工电离层加热条件下,反射高度的电波能量吸收率的理论估算十分困难。利用稳态的电子动量方程和能量方程,结合2009年8月电离层加热实验中非相干散射雷达实测的电子密度、电子温度和离子温度对反射高度附近的电波能量吸收率进行了估算。根据计算结果,可以得到显著的电波能量吸收率的空间分布结构,能量吸收基本呈近高斯分布,但结构在横向和纵向上并不沿能量吸收中心对称。电波能量吸收率与电离层参量的空间分布特征没有直接的对应关系,但幅度值的相关关系明显。与吸收率相比,由于吸收与损失的物理机制不同,损失率的空间分布范围更广。对电波能量吸收率的统计分析结果表明:泵波频率接近临界频率时,能量吸收中心偏离场向的方差越小,亦更接近反射高度。0.6 MHz附近,电波能量吸收率随频差变化的曲线存在锐边界,在0.6MHz以下,随频差增大线形增加,0.6 MHz以上,随频差增大电波能量吸收率缓慢下降。从电波能量吸收率幅度的统计结果可以得出,并非加热频率愈接近峰值频率吸收效果愈佳,而是临界状态下时(两组加热机制的交界)才会取得最佳的加热效果。
文中给出了使用非相干散射雷达数据推算出的电波能量吸收率,在此基础上,进一步细致分析各种不稳定性的发生条件,区分混杂谐振、参量不稳定性和回旋谐振等不同的机制对加热效应的贡献,进而建立描述多机制的加热问题的电波能量吸收率的经验和半经验模型是我们进一步所要完成的工作。
[1]GUREVICH A V.Nonlinear Phenomena in the Ionosphere[M].Berlin:Springer,1978.
[2]叶公节,刘兆汉.电离层波理论[M].北京:科学出版社,1983.
[3]XU Bin,WU Jian,WU Zhensen,et al.The temperature enhancement induced by ionosphere heating in low region[J].Progress in natural science,2008,18(11):1339-1343.
[4]黄文耿,古士芬.大功率无线电波与低电离层的相互作用[J].空间科学学报,2003,23(3):181-187.HUANG Wengeng,GU Shifen.Interaction between the powerful high-frequency radio wave and the lower terrestrial ionosphere[J].Chinese Journal of Space Science,2003,23(3):181-187.(in Chinese)
[5]BANKS P.Collision frequency and energy transfer-electrons[J].Planetary and Space Science,1966,14(11):1085-1103.
[6]BANKS P.Collision frequencies and energy transfer-ions[J].Planetary and Space Science,1966,14(11):1105-1122.
[7]STUBBE P,VARNUM W S.Electron energy transfer rates in the ionosphere[J].Planetary and Space Science,1972,20(8):1121-1126.
[8]STUBBE P.A new collisional relaxation model for small deviations from equilibrium[J].Journal of Plasma Physics,1987,38(1):95-116.
[9]BERNHARDT P A,DUNCAN L M.The feedbackdiffraction theory of ionospheric heating [J].Journal of Atmospheric and Solar-Terrestrial Physics,1982,44(12):1061-1074.
[10]倪彬彬,赵正予,项 薇,等.高频泵波加热电离层的数值模拟[J].电波科学学报,2004,19(3):274-279.NI Binbin,ZHAO Zhengyu,XIANG Wei,et al,Numerical modeling of ionospheric modification with powerful HF pump waves[J].Journal of Radio Science,2004,19(3):274-279.(in Chinese)
[11]黄文耿,古士芬.大功率无线电波与高电离层的相互作用[J].空间科学学报,2003,23(5):343-350.HUANG Wengeng,GU Shifen.The heating of upper ionosphere by powerful high-frequency radio waves[J].Chinese Journal of Space Science,2003,23(5):343-350.(in Chinese)
[12]黄文耿,古士芬,龚建村.大功率高频无线电波加热电离层[J].电波科学学报,2004,19(3):296-301.HUANG Wengeng,GU Shifen,GONG Jiancun.Ionospheric heating by powerful high-frequency radio waves[J].Journal of Radio Science,2004,19(3):296-301.(in Chinese)
[13]KERO A,BOSINGER T,POLLAR P,et al.First EISCAT measurement of electron-gas temperature in the artificially heated D-region ionosphere [J].Annales Geophysicae,2000,18(9):1210-1215.
[14]LOFAS H,IVCHENKO N,GUSTAVSSON B,et al.F-region electron heating by X-mode radio-waves in under-dense conditions[J].Annales Geophysicae,2009,27(6):2585-2592.
[15]徐 彬,王占阁,薛 昆,等.极区二维人工电离层加热数值仿真[J].电波科学学报,2010,25(1):1-6.XU Bin,WANG Zhange,XUE Kun,et al.2Dnumerical simulation of artificial ionospheric heating in polar region[J].Journal of Radio Science,2010,25(1):1-6.(in Chinese)
[16]徐 彬,王占阁,吴 军,等.2009年夏季极区电离层加热实验研究[J].极地研究,2010,22(4):334-347.XU Bin,WANG Zhange,WU Jun,et al.Observation of the polar ionospheric heating experiment in summer,2009 [J].Chinese Journal of Polar Research,2010,22(4):334-347.(in Chinese)
[17]HEDIN A E.Extension of the MSIS thermospheric model into the middle and lower atmosphere[J].Journal of Geophysical Research,1991,96(A2):1159-1172.
[18]BILITZA D.International reference ionosphere—status 1995/96[J].Advances in Space Research,1997,20(9):1751-1754.
[19]BLAGOVESHCHENSKAYA N F,CARLSON H C,KORNIENKO V A,et al.Phenomena induced by powerful HF pumping towards magnetic zenith with a frequency near the F-region critical frequency and the third electron gyro harmonic frequency[J].Annales Geophysicae,2009,27(1):131-145.

