具有极化特征的植被相干散射模型及参数反演
胡楚锋 周 洲 李南京 张麟兮 许家栋
(1.西北工业大学无人机特种技术国家级重点实验室,陕西 西安 710065;2.西北工业大学航空学院,陕西 西安 710072)
引 言
无论是森林植被的资源管理,还是农作物的估产,雷达遥感技术已成为大尺度环境变化实时监测的重要手段之一。为了解决植被遥感逆问题,从测量数据中反演出植被的物理参数,建立合理准确的理论模型至关重要。通常,适合进行参数反演的模型需要满足:1)正确性,即它包含足够的物理参数来解释和预测可观测的现象和数据。2)简单性,即在有限观测值的情况下,能确定需要反演的参数。自从1997年Cloude和Papathanassiou发现干涉相干性强烈受极化的影响,并提出了极化干涉相干最优理论[1]。随后,国内外研究学者广泛开展了在极化干涉SAR测量条件下进行植被参数提取的研究。2000年,Treuhaft建立了植被物理参数和极化干涉雷达相干系数之间的相干散射模型[2],其在物理结构及模型复杂度上进行了很好的折衷,特别适用于反演地表植被参数。
相干散射模型采用离散体方法,将植被看作随机离散体,通过计算后向散射和二次辐射场获得相干函数,最初建立的模型为单一植被体的模型。随后Cloude在此基础上提出了随机体及地表二层相干散射模型[3],取得了良好的效果。文献[4]推导了地表-树干-树冠三层相干散射模型,但模型未涉及植被的极化特征。文献[5]讨论了二层模型在农作物方面(如水稻具有明显的垂直极化特征)的一些限制,初步分析了极化特征对模型的影响。国内从2000年以后也开展了大量植被参数反演的工作,但主要集中于反演算法的研究[6-7]。因此,建立具有极化特征的相干散射模型对于拓展极化干涉雷达的应用领域具有重要的理论意义。
针对形态分布具有极化特征的植被,在植被体及地表二层相干散射模型的基础上,将衰减系数定义为极化的函数,增加了四个极化通道的信息,形成了具有极化特征的二层相干散射模型,将模型的有效解域由“线”变“面”。在参数反演的过程中,采用三阶段法,通过曲线拟合、地形相位判断、高度估计,结合计算平均高度和标准差的方法反演出植被高度。实验在环境可控的微波暗室中进行,采用极化干涉SAR半实物系统[8],获取由多棵具有明显极化特征南洋杉的极化干涉回波数据,并利用所建模型进行参数反演,获得的植被高度与真实值的误差仅为0.03m,说明了该模型的有效性。
1.具有极化特征的相干散射模型
在植被体相干散射模型的基础上,考虑地面反射及植被和地表之间的互相作用,用一个二层函数模型来描述,如图1所示。

图1 植被体及地表二层模型示意图
植被体及地表二层相干散射模型由两部分构成:下半部分是具有一定厚度z0的地表层,在地表层上是高度为hv的植被层,根据目标分解理论[9],描述目标极化特征的散射相干矩阵T(z)由地表散射和植被体散射两部分构成,即
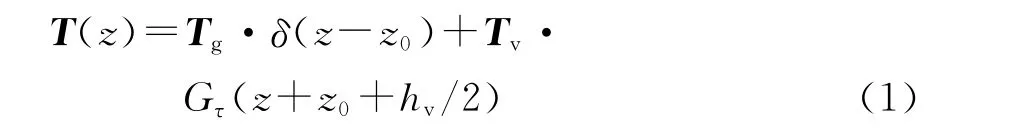
式中:Tg和Tv分别是地表和植被体散射相干矩阵;δ(·)是脉冲函数;Gτ(·)是矩形门函数;它们对应的表达式为

考虑具有极化特征的植被体,其衰减系数与极化相关,假设发射和接收的衰减系数分别表示为σT(ω)和σR(ω),从极化空间中选择一单位复矢量ω作为投影矢量,则极化干涉复相干系数为

式中:Ω12由基线两端的极化散射矩阵获得

式中:φ0是与地形z0相关的相位;kz为直角坐标系下的垂直波数;θ为平均入射角;hv是植被体的高度。
式(4)中T11和T22是基线两端的极化相干矩阵,在不考虑时间去相关的情况下,两者相等。它们可由式(5)获得,即当基线距趋于0时(kz,φ0→0)

对于具有极化特征的植被体来说,电磁波极化在植被体的传播过程中随距离z变化,即ω=ω(z).由前面的讨论可知,仅当发射极化为特征极化时,此时的极化特征是与衰减系数最大和最小值对应的。为了简化,在以下公式中假定ω是一个与距离无关的定值。由于衰减系数通常以求和形式出现,因此,可定义一个等效衰减系数

式中的下标ω保持了对极化的依赖性。
由前可知,地面相当于一个反射对称目标,具有极化特征的植被体形态同样可看成是反射对称,所以其相干矩阵如式(8)、(9)所示

于是式(5)和式(6)变为

所以复干涉相干系数为
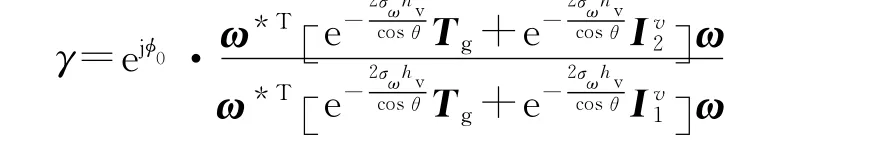
式(14)可写成

式中:体相干系数γv和地体幅度比μ分别为

由于这两个函数以两种方式依赖于极化。第一种,所选的极化组合仅与相干矩阵Tg和Tv中的元素相结合。第二种,不同的衰减系数σω与所选极化ω有关。然而,当选择了一种特定的极化,体相干系数γv的分子和分母中具有相同的指数项exp(-σωhv/cosθ),以及相干矩阵Tv,所以体相干系数简化为衰减系数的函数,其表达式为

另一方面,由于地体幅度比代表分子(地表)和分母(植被体)不同的相干矩阵,它表示地面回波和植被体回波的能量比值关系,难以进行如前的简化。因此,具有极化特征的植被体二层模型的复相干系数最终可表达为

式中,0≤L(σω,ω)≤1.与随机体覆盖地表的情况不同,由于体相干系数γv与极化相关,所以式(19)在复平面内不是一条直线,而是一个区域。
2.模型的物理解释
与随机体及地表二层模型不同,具有极化特征的植被二层相干散射模型的衰减系数与极化相关,所以式(19)在复平面内不是一条直线,而是一个区域,如图2所示。
模型的物理解释如下
1)由于衰减系数与极化状态有关,因而对于每个极化通道来说,体相干系数也不一样,它们分别对应着不同的直线,根据地体幅度比从0到无穷大的变化范围,可以看出,有向体及地表二层模型的复相干系数分布在一个近似于三角形的区域内。
2)有效区域的宽度除了与衰减系数的范围有关,还与垂直波数和森林高度的乘积kz·hv有关,当两者乘积变大时,有效区域的宽度也随之增加。
3)最大和最小的衰减系数分别对应着特征极化,因此,对应于特征极化的复相干系数是有效区域的边界。

图2 模型示意图
3.模型的室内验证实验分析
该系统在西北工业大学无人机特种技术重点实验室的综合性能测试屏蔽暗室内搭建完成,主要由取样架、矢量网络分析仪(加功放)、双脊喇叭天线、转台及场景五部分组成。矢量网络分析仪和4个双脊喇叭天线构成了整个雷达系统,可以同时发射和接收两路信号,天线向下倾斜,保持45°的入射角,场景由九棵具有垂直结构的树正方形排布,天线距离中心的距离为7m,系统构成如图3(a)所示。
测量的南洋杉如图3(b)所示,中间树干的高度为1.5m,直径约为2.5cm,树干每隔一定的距离有5~6个长约0.5cm的树枝构成,每个树枝的直径大约为1cm,顶端的树枝与树干约60°的夹角,越接近底端时,夹角越来越接近90°.在每根树枝上都长有由许多针状物构成的树叶,其分布也具有水平极化特征。
实验中,测试样品绕着垂直轴在方位向上旋转360°,获得了120个角度间隔3°的全极化后向散射频域数据。系统采用网络分析仪的步进频率体制进行测量,测试的频率范围是3~10GHz,频率间隔为10MHz,在频域所获得的原始数据是减去了空暗室的频域数据之后,通过时域门来隔离目标响应与天线耦合及暗室杂波。然后,采用一个金属球和二种不同旋转角度下的二面角作为参考目标进行全极化校准。该测量系统的校准精度在0dBsm时幅度误差优于0.5dB,相位误差优于5°.测量的敏感度取决于单频点的平均次数和时域门的宽度。

原始数据获取了两条基线下样品的极化散射矩阵SHH、SHV、SVH、SVV,根据复相干系数的定义(如下式),可以计算出γHH、γHV(假设γHV=γVH)、γVV、γHH+VV、γHH-VV的大小。

式中,S1和S2分别表示上基线和下基线的后向散射测量值。对于整个样品来说,假定它由许多个散射体构成,并且每一个散射体都具有独立的相干特性,那么式(20)中的相干系数估计就可用空间平均来代替集合平均。因此,通过转台旋转一圈后对样品的多次采样进行空间平均获得了不同极化通道的复相干系数。
除了以上获得的5个复相干系数,采用相干最优化算法来寻找极化空间中具有最佳相干性的复相干系数,通过增加复相干系数的个数可以提高直线拟合的精度。由此,一共得到8个复相干系数,将它们画在复平面单位圆内,便可根据这些复相干系数进行最小二乘直线拟合。采用具有极化特征的植被体二层模型进行参数反演,由下式计算垂直波数的大小

式中:B为测试的基线距;λ为测试波长;θ为入射角;R是天线距离样品中心距离。当测试频率为4.5GHz时,采用三阶段法对地形相位和植被高度进行估计,反演过程如图4所示。

图4 参数反演结果
第一阶段给出了由8个不同的干涉相干值以及根据最小二乘法进行拟合的直线,如图4(a)所示,该直线与单位圆相交于两点。
第二阶段如图4(b)所示,由γHH-VV的位置可知:与单位圆的交点(0.994,-0.099)是真实的地形相位点,这一点对应的地形为-0.1186m.从该点出发,与最大和最小相干点相连,由此确定了相干系数的取值范围。
第三阶段根据体相干函数的表达式,衰减系数的范围从0.3dB/m到2dB/m,如图4(c)所示:画出以这两个衰减系数为边界、植被高度hv为变量的两条曲线,与上一阶段中的两条直线相交,形成了一个类似于四边形的有效解域。在解域中取9个有效值,计算其平均值和标准差,得到的结果分别为1.33m和0.2m,估算的结果与实际高度误差为0.03m.
4.结 论
在植被体相干散射模型的基础上,结合目标分解理论,分析了具有极化特征的植被及地表极化干涉回波特征。考虑地面的影响,推导了极化干涉相干系数与植被高度、衰减系数、地形相位等参数之间的数学关系,以衰减系数作为极化分量的函数,建立了具有极化特征的植被及地表二层相干散射模型。
在微波屏蔽暗室内搭建了极化干涉半实物合成孔径雷达成像系统,对模型进行了实验验证,测量了包含植被、地面的真实场景,考虑植被结构有向分布的特点,采用相干最优极化算法,增加极化干涉相干系数,将有效解的范围扩展为一个区域,通过求平均值和标准差的方法反演植被的高度。实验结果表明:在地体幅度比小于-10dB的情况下,最终获得的结果与实际高度的误差仅为0.03m,说明了模型的有效性,也为极化干涉雷达在植被参数估计方面的应用提供了重要手段。
[1]CLOUDE S R,PAPATHANASSIOU K P.Polarimetric optimization in radar interferometry[J].Electronics Letters,1997,33(13):1176-1178.
[2]TREUHAFT R N,SIQUEIRA P R.Vertical structure of vegetated land surfaces from interferometric and polarimetric radar[J].Radio Science,2000,35(1):141-177.
[3]CLOUDE S R,PAPATHANASSIOU K P.Threestage inversion process for polarimetric SAR interferometry[J].IEE Proc Radar Sonar Navig,2003,150(3):125-134.
[4]NEUMANN M,FERRO L,REIGBER A.Estimation of forest structure,ground,and canopy layer characteristics from multibaseline polarimetric interferometric SAR data[J].IEEE Trans Geosci Remote Sensing,2010,48(3):1086-1104.
[5]LOPEZ J M,BALLESTER J D,MARQUEZ Y.Model limitations and parameter-estimation methods for agricultural applications of polarimetric SAR interferometry[J].IEEE Trans Geosci Remote Sensing,2007,45(11):3481-3493.
[6]范立生,高明星,杨 健,等.极化SAR遥感中森林特征的提取[J].电波科学学报,2005,20(5):553-556.FAN Lisheng,GAO Minxing,YANG Jian,et al.Feature extraction of a forested area based on polarimetric SAR[J].Chinese Journal o f Radio Science,2005,20(5):553-556.(in Chinese)
[7]李廷伟,梁甸农,黄海风.植被分布式SAR极化干涉复相关系数建模与分析[J].电波科学学报,2010,25(3):415-421.LI Tingwei,LIANG Diannong,HUANG Haifeng.Modeling and analyzing complex coherence for vegetation observed by distributed polarimetric SAR interferometric system[J].Chinese Journal of Radio Science,2010,25(3):415-421.(in Chinese)
[8]胡楚锋,许家栋,李南京,等.全极化SAR半实物仿真系统[J].系统工程与电子技术,2010,32(7):1537-1539.HU Chufeng,XU Jiadong,LI Nanjing,et al.Full-polarization synthetic aperture radar(SAR)hard-in-loop system[J].System Engineering and Electronics,2010,32(7):1537-1539.(in Chinese)
[9]CLOUDE S R,POTTIER E.A review of target decomposition theorems in radar polarimetry[J].IEEE Transaction on Geoscience and Remote Sensing,1996,34(2):198-518.

