Hölder型矩阵不等式及改进
黄 灿
(重庆大学数学与统计学院,重庆 400044)
Hölder不等式在数学定理的证明过程中起着重要的作用[1-2]。王松桂[3]给出了半正定Hermite矩阵迹的Hölder不等式成立的充要条件。设A,B为n×n阶半正定Hermite矩阵,A≠0,B≠0,p>1,1/p+1/q=1,则 trA1/pB1/q≤(trA)1/p(trB)1/q,等号成立⇔∃k >0,使得 B=kA。本文利用 Fuad[1]给 Young 不等式加细的技巧对该结论进行改进,得到了实对称矩阵迹加细的Hölder不等式成立的充要条件。Young不等式、Hölder不等式及Minkowski不等式是几个重要的不等式。本文在文献[1]和文献[3]的基础上进一步将它们推广。
1 预备知识
Young不等式:若 a,b>0,p>1,1/p+1/q=1,则有

Hölder不等式:若 p>1,1/p+1/q=1,则有

2 主要结果
定理1 加细的Hölder不等式为

两边同时乘X1/pY1/q。即得结论。
定理2 加细的矩阵Hölder不等式:设A,B为n×n阶实对称正定矩阵,p>1,1/p+1/q=1,则
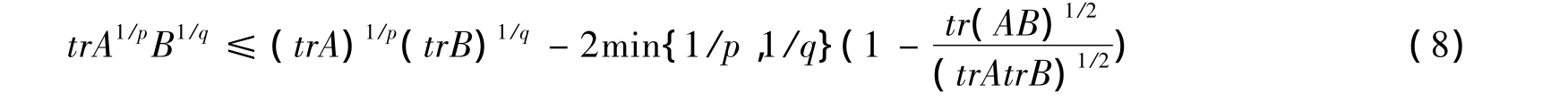
等号成立⇔∃k>0,使得B=kA。

[1]Fuad Kittaneh,Yousef Manasrah.Improved Young and Heinz inequalities for matrices[J].Math Anal Appl,2010,361:262-269.
[2]刘玉琏.数学分析讲义:上[M].北京:高等教育出版社,2003.
[3]王松桂,吴密霞,贾忠贞.矩阵不等式[M].北京:科学出版社,2006.
[4]Horn R A,Johnson C R .Matrix Analysis[M].Cambridge:Cambridge University Press,1985.
[5]魏佳丽,郭辉.利用凸函数证明Hölder不等式[J].重庆工商大学学报:自然科学版,2009(6):540-542.
- 重庆理工大学学报(自然科学)的其它文章
- 制造型企业BOM模块化技术
- 《重庆理工大学学报》“化学化工”栏目征集稿件
- 基于Adams的传输链仿真分析

