汽车螺纹联接件预紧力的优化设计1)

章伊华 侯培海 杨国玉

(宁波大红鹰学院汽车CAE应用技术研究所，宁波，315715)

螺纹联接结构是汽车部件之间的主要联接方式，被广泛应用于汽车结构中，如发动机气缸盖联接、悬架系统各部件之间联接、轮毂联接等[1]。随着对汽车安全性能要求的提高，加之复杂的工作状态，螺纹联接的优化设计已成为当今工程设计中十分重要的环节。螺纹联接中的预紧力对联接结构的强度及使用寿命起至关重要的作用[2－3]。标准螺纹联接的预紧力大小可以从一些工程设计手册中查到。然而，这些数据大多基于传统的解析方法和试验，缺乏对螺纹联接内部应力状态的了解，尤其是无法确定螺纹根部应力集中区域的最大应力，因此，无法对螺纹联接中的预紧力进行优化设计。

近年来，一些专家学者借助有限元方法对螺纹联接应力进行分析预测[4]，找出控制螺栓联接预紧力的方法[5]，并对联接螺栓断裂失效进行分析[6]，取得了可喜的成果。但由于三维螺旋螺纹结构的复杂性，给有限元模拟带来巨大的困难，从而限制了利用有限元对螺纹联接结构数值模拟的发展。

笔者基于已有研究成果，考虑螺纹联接中复杂的接触、摩擦、预紧等非线性因素，对三维螺旋螺纹结构进行合理简化，在没有损失3D精度的条件下简化为二维轴对称问题，同时对应力集中区细化，减少了计算量。在螺纹接触的应力集中区，这种方法比用3D方法更加准确。运用此二维轴对称有限元模型，通过对多种工况的分析总结，找出螺纹最大应力随外力和预紧力的变化规律及材料塑性应变对螺纹联接有效寿命的影响;并通过纯弹性假设，分析材料应力变化与预紧力和外力的关系，找出螺纹联接的最佳预紧力范围。

1 有限元模型建立

选用一副实际工程中的高强度螺栓联接件作为研究对象。螺栓、螺母及连接件材料属性相同，弹性模量 E=2.07 ×105MPa，泊松比 μ =0.3，屈服极限 σs=924 MPa，强度极限 σb=1130 MPa，延伸率 δ=5%。对螺纹区域进行应力分析时，螺纹的变形往往会超过弹性范围，因此同时考虑弹性变形和塑性变形。

利用ABAQUS软件进行建模和分析，分析对象为螺纹联接件。螺纹规格为ISO公制标准三角形螺纹M10×1.5。根据螺纹联接的结构和受力特点，在有限元建模时引入以下假设和简化:①接触螺纹之间考虑为库伦摩擦接触关系;②采用轴对称结构，利用三角形和四边形混合单元划分网格，对螺纹接触区域单元进行局部细化，共生成8087个单元，8450个节点，如图1所示。

操作中分两个步骤施加载荷:第一步，施加预紧力，使整个接头形成预紧接触状态，计算预紧状态下的应力和变形;第二步，施加轴向外力，计算接头在轴向外力作用下的应力和变形。

2 结果与分析

2.1 螺纹最大应力与预紧力的关系

螺栓的预紧力对螺栓总载荷、临界载荷以及接合面密封能力产生影响。对于受轴向载荷的螺栓联接，预紧力使接合面上产生压紧力，外载荷作用下的残余预紧力是接合面工作时的压紧力。预紧力不足将会导致接合面分离，甚至引起强烈的横向振动，以致螺母松动;预紧力过大则螺纹内部屈服甚至断裂、螺栓被拧断，联接件有可能被压碎。因此研究预紧力作用下螺栓联接处的最大应力十分必要。表1为根据FEA模型计算得出的不同预紧力下螺纹最大应力值。

图1 有限元模型

表1 不同预紧力下螺纹最大应力值

由有限元计算可知:螺纹联接中各圈螺纹上的应力分布不均匀，螺栓第一圈、第二圈螺纹根部所受应力最大，这与普遍试验和工程事故的结果相吻合，如图2、图3应力云图所示。图4为计算输出的螺纹应力随预紧力变化曲线，最大应力达到屈服强度以前，螺纹段的最大应力与轴向预紧力基本呈线性增长关系;继续增加预紧力，金属开始从弹性状态非均匀地向弹—塑性状态过渡;进入屈服后，最大应力随预紧力增加先小幅波动，继而呈非线性增长关系;达到强度极限时，螺纹根部产生裂缝直至断裂破坏，造成整个螺纹联接的失效。因此在进行螺纹连接预紧力设计时，首先应防止螺纹预紧力过大而造成损坏。

2.2 塑性应变与螺纹强度的关系

材料在塑性阶段，除存在可恢复的弹性应变外，还存在不可恢复的永久塑性应变。当应力移去，弹性应变消除，但塑性应变仍然存在，材料从屈服到破坏是一个塑性变形不断累积的过程。位移或应变的极限值可充分反映材料抵抗破坏的能力，材料应变破坏准则可表达为:

式中:εe为弹性应变;εp为塑性应变;εf为极限应变。当满足上式时，即认为该点的应变达到极限值，材料破坏失效[7－8]。

图2 13 kN预紧力下应力云图

图3 32 kN预紧力下应力云图

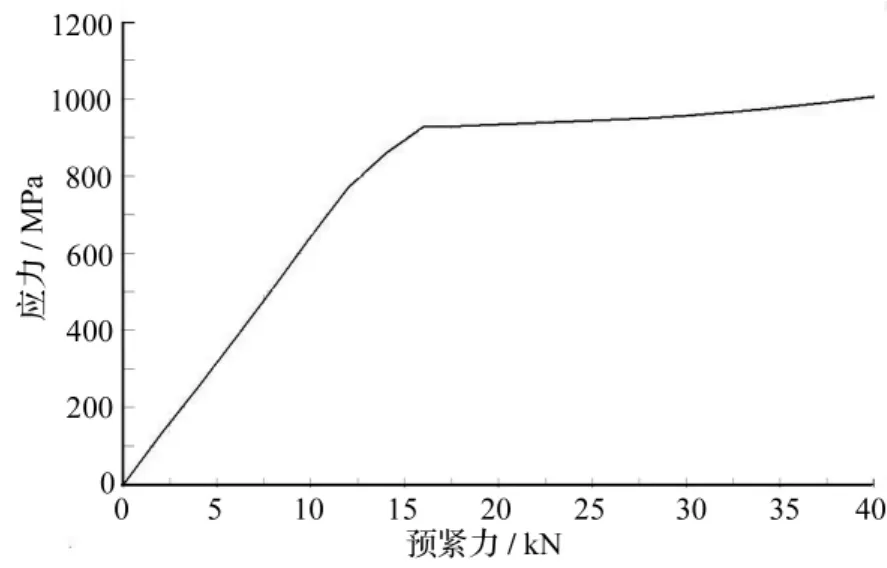
图4 应力随预紧力的变化曲线

如预紧力Qp为20 kN时，螺纹联接的最大应力为933.6 MPa，超出材料屈服极限924 MPa。图5给出最大承载单元的应力随外力变化曲线，可见应力随外力先保持小幅平缓增加，当加载达到临界点33 kN时，应力曲线大幅上升应变也随之上升，到达最大值1005 MPa时，变化率为5.86%。

图6给出20 kN预紧力下，外力分别为20、28、36、40 kN时，螺纹联接的应力云图，整个加载过程中，由于材料处于屈服阶段，塑性变形不断积累，严重影响螺纹联接强度和有效寿命，所以保证螺纹实际工况的最大应力小于屈服极限是预紧力设计的重要前提。

图5 20 kN预紧力单元应力变化曲线

图6 预紧力20 kN下不同外力产生的最大应力

3 最佳预紧力的优化设计

3.1 纯弹性条件假设

为了便于分析，先将问题简化，假设材料为纯弹性钢材料，忽略钢材料的屈服极限影响。最大外力设置为40 kN。在给定预紧力下，通过分步求解而逐渐增加外力，并输出每步的最大应力值。将不同预紧力情况下最大应力与外力的关系表示出来。从表2可见不同预紧力下接触面分离时的外力。图7显示，预紧力为零时，接触面一直处于分离状态，螺纹上的最大应力与外力基本成线性关系，应力随外力的增大而增大，如图中实线所示;施加预紧力后，螺纹上产生初始应力，随着外力的增加，螺纹上最大应力先平缓增加，达到实线后，螺纹最大应力随实线大幅上升，即预紧力曲线沿实线大幅上升，此时预紧力消失，接触面开始分离。预紧力越大抵抗外力工作载荷的能力越大，如表2数据所示:当预紧力为11 kN时，外力载荷在12 kN以下能有效保证螺纹联接的工作安全;当预紧力为22 kN时，外载荷在25 kN以下也是安全有效工作的;达到25.9 kN临界点时，残余预紧力消失，螺栓联接接触面开始分离，此后最大应力随着外力的增加而快速提升。如果不考虑材料屈服极限的限制，22 kN的预紧力承受25 kN的最大外力是理想状态。

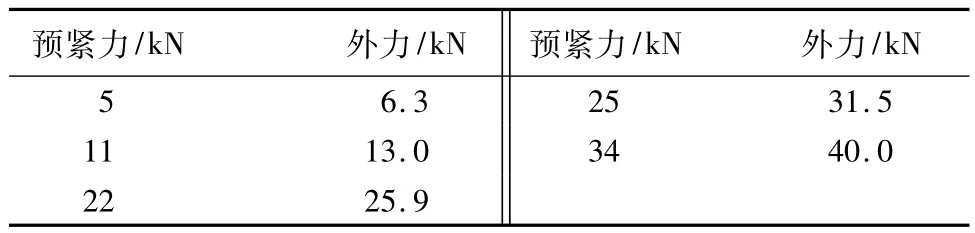
表2 不同预紧力下接触面分离时的外力

3.2 实际螺纹结构的最佳预紧力及最大可承载外力

传统设计手册中10.9级M10螺栓预紧力计算式为:

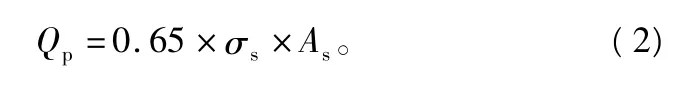
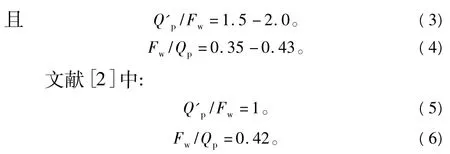
式中:Q'p为残余预紧力;Fw为外力[9－10]。上述两种方法都是类同于传统法的保守取值，没有精确计算出结构的预紧力和有效承载能力。

图7 最大应力随预紧力和外力的变化曲线

图8显示了真实材料下螺纹联接最大应力与预紧力和外力关系。通过有限元优化设计与分析得出最佳预紧力为12 kN，此时初始最大应力为830 MPa，确定最大工作载荷14 kN，与此对应螺纹最大应力为900 MPa，小于材料屈服极限。工作过程中结构最大应力始终保持高位，但不超过屈服极限，既满足极限载荷要求，又能保证有效寿命安全。螺纹中的最大应力随外力保持平缓增长，材料强度充分利用，结构受力合理，距接触面分离点16 kN有一定距离，保证了足够的残余预紧力。

图8 应力与预紧力和外力的关系

如果减小预紧力则会造成外力达到最大时，接触面分离。预紧力过大，即使无外力作用，材料却已经超出屈服极限，如预紧力为25 kN时的预紧力曲线，初始最大应力950 MPa，大于材料屈服极限，不符合预紧力设计原则。因此，最佳预紧力设计首先要满足预紧力曲线初始应力为屈服极限的85%～90%;其次，对应的有效最大工作载荷应为预紧力的1.17～1.25倍，上述二点即是预紧力设计的重要依据和准则。如果已经满足上述二点继续增加预紧力，只会无效地增大螺纹联接的应力，从而提高对结构几何参数或材料性能的要求，增加不必要的成本。

4 结论

预紧力作用下，材料依次经历弹性阶段、屈服阶段以及强化断裂阶段，最大应力集中在螺母第一圈、第二圈的螺纹根部。随着预紧力的不断增加，当最大应力达到强度极限时，会造成螺纹根部的断裂破坏。因此，设计螺纹联接预紧力时，应首先避免螺纹在预紧过程中的损坏。

预紧力过大使得无外力作用时材料进入屈服区间，随着外力的增加，最大应力变化不大，但屈服区间的不断变大却极度影响使用寿命。因此螺纹联接中最大应力小于材料屈服极限是保证安全运行的基础条件，也是预紧力设计的基本原则。

基于有限元分析，通过纯弹性条件假设找出弹性区预紧力曲线随外力变化的一般规律，再以实际材料的有限元模型进行优化设计，得出螺纹联接最大应力与预紧力和外力的关系曲线。通过分析求出最佳预紧力和最大有效承载能力，并获得最佳预紧力设计的二个基本准则，既节省材料并满足极限载荷要求，又能保证有效寿命，对工程结构设计及校核具有重要的参考意义。

[1]成大先.机械设计手册[M].北京:化学工业出版社，2011.

[2]Huang Y H，Quan C，Tay C J，et al.Shape measurement by the use of digital image correlation[J].Optical Engineering，2005，44(8):1－7.

[3]Ghorashi M，Inman D J.Shape memory alloy in tension and compression and its application as clamping force actuator in a bolted joint:Part2-Modeling[J].Journal of Intelligent Material Systems and Structures，2004，15(8):589 －600.

[4]王旱祥，于艳艳，李增亮，等.锥度对油管螺纹联接应力影响的有限元分析[J].石油机械，2007，35(9):55 －58.

[5]赵曼.控制螺栓连接预紧力的方法[J].水力电力机械，2006，28(7):36－38.

[6]陈伟，冯小红，王进京.联接螺栓断裂失效分析[J].通用机械，2007(1):82－84.

[7]卜炎.螺纹连接设计与计算[M].北京:高等教育出版社，1995.

[8]王志礼.基于动态检测的螺纹拧紧设备的研制[D].合肥:合肥工业大学，2007.

[9]尹益辉，余绍蓉.基于3D有限元模拟的螺栓接头变形—内力关系及在设计中的应用[J].机械强度，2008，30(6):947－952.

[10]何玉林，雷增宏，石秉楠.MW级风力发电机组轮毂连接螺栓接触强度分析[J].现代制造工程，2011(4):102－102.