空间6R机械臂圆弧轨迹规划及仿真

吕 燕，安 凯

（山东航天电子技术所，山东 烟台 264003）

0 引言

传统轨迹规划分为关节空间的规划和在笛卡尔空间的规划两种。其中：关节空间的轨迹规划相对简单，且不会出现奇异位形，但末端的运动轨迹不直观；笛卡尔空间的轨迹规划较直观，但在规划过程中易产生奇异位形，同时其运动学逆解也相对复杂。圆弧运动是机器人完成点到点运动的常用运动方式，研究具有普遍意义。某6R机器人由6个回转关节组成，机器人末端装有机械手，用于完成操作任务，如安装相机执行拍摄任务，抓取物体，协助交会对接等。在机械臂末端执行任务时，为有效避开障碍物，防止抓手与障碍物碰撞、发生抓手或者障碍物的损坏等，本文基于文献［1］的机器人圆弧轨迹规划方法，对在笛卡尔空间的圆弧运动轨迹规划进行了研究。

1 运动学分析

用D－H法对机器人建模，如图1所示，杆件参数见表1［2］。其中：ai－1，αi－1，di，θi分别为D－H建模法中按运动顺序，由本坐标系变换至下一坐标系的旋转角度和平移长度。

图1 6R机器人模型Fig.1 6R－robot model

运动支架各连杆的参数为：d1＝135mm，d2＝50mm，d4＝－50mm，a2＝1 050mm，a3＝800mm。

机器人正运动学解是已知各关节的角度值，由运动学算法计算机械臂末端的位置和姿态。只要机器人的关节变量已知，就能根据运动学方程确定机器人的位置。

表1 D－H参数表Tab.1 D－H parameters

运动学逆解是已知关节末端期望的位置和姿态，由变量分离法求出各关节的转动角度。本文模型中，因构型特殊，求解较易。在多组解中，本文选取一组合适的解作为最终解。

2 圆弧运动轨迹规划

2.1 位置插补

空间圆弧轨迹的参数方程的编写难度极大，对空间圆弧轨迹方程进行插补也非常复杂。为便于计算圆的轨迹方程，须先将圆的轨迹方程由固定坐标系进行变换，在新坐标系中引入轨迹规划插值后，再反变换到基准坐标系中［3］。其轨迹规划流程如图2所示。

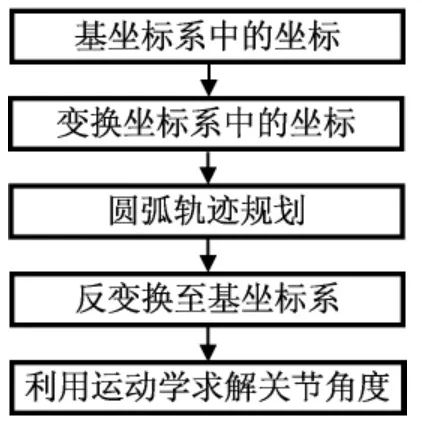
图2 机器人圆弧运动轨迹规划Fig.2 Robot’s round track programming

设已知起始点P1在基坐标系O－XYZ中的位置为（x1，y1，z1），终点P3在O－XYZ系中的位置为（x3，y3，z3），指定的路经点P2在O－XYZ系中的位置为（x2，y2，z2）。

此时，可由空间O－XYZ系中的P1，P2，P3三点确定一空间平面M，由线段P1P2的中点可确定与P1P2垂直的一平面T，由线段P2P3的中点可确定与线段P2P3垂直的一平面S，如图3所示。

图3 坐标空间关系Fig.3 Relationship of two reference frames

平面M的方程可表示为

平面T的方程可表示为

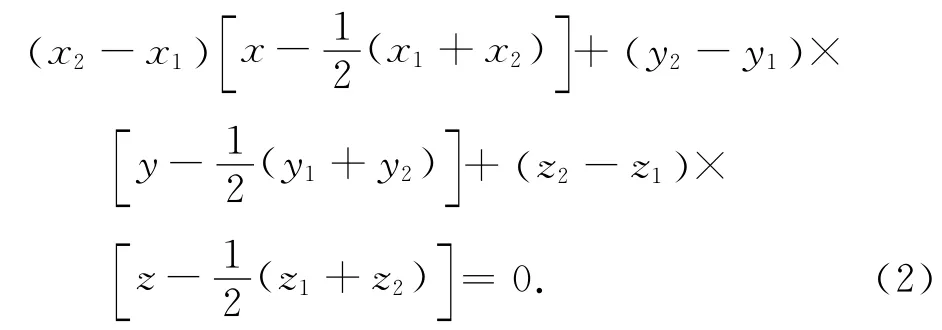
平面S的方程可表示为

联立式（1）～（3），用高斯消去法可求出圆心P0（x0，y0，z0），进而可求得半径

以P0为原点，将M平面法矢量方向作为新坐标系的Z0轴方向，P0P1方向作为新坐标系的X0轴方向，新坐标系的Y0轴的方向余弦为Z0轴的方向余弦叉乘X0轴的方向余弦，建立新坐标系P0－X0Y0Z0。只要求出P0－X0Y0Z0系在O－XYZ系中的变换矩阵A，就可通过坐标变换将三维空间的圆弧变换到二维平面的圆弧，如图4所示。图中：分别为点P1，P2，P3在P0－X0Y0Z0系中的坐标。

由式（1）可得平面M的法矢量方向数为

图4 M平面上圆示图Fig.4 Circle on M－reference－plane

以M平面法矢量方向作为新坐标系的Z0轴方向，Z0轴的方向余弦为

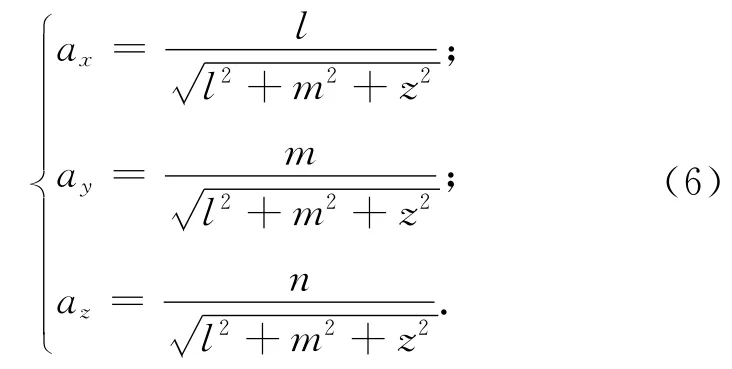
以P0P1方向作为P0－X0Y0Z0系的P0X0轴方向，则P0X0轴的方向余弦为

P0－X0Y0Z0系的P0Y0轴的方向余弦为

从而可求出P0－X0Y0Z0系与在O－XYZ系的变换矩阵分别为

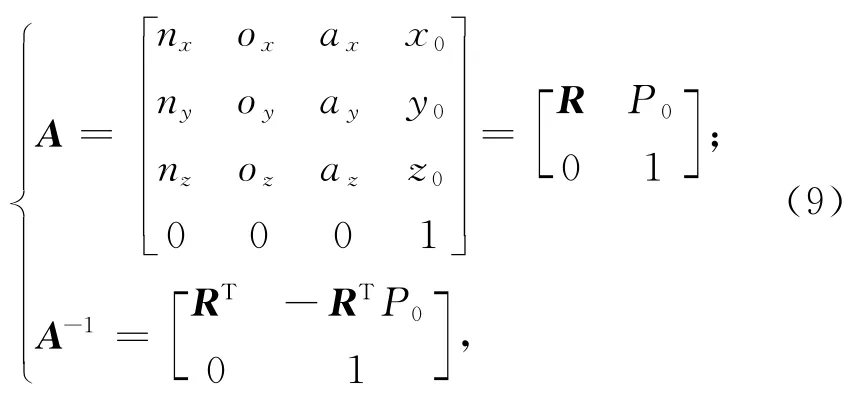
进而可得点P1，P2，P3在P0－X0Y0Z0系中的坐标为

式中：i＝1，2，3。在平面M上，已知Q1，Q2，Q3三点坐标，易求得P0Q1、P0Q2间的夹角θ1，P0Q2、P0Q3间的夹角θ2，以及由点Q1经点Q2到点Q3的弧s＝r（θ1＋θ2）。

在M平面上进行圆弧插补计算：由设定的末端线速度v可得运动时间t＝s／v和运行步数N＝tΔt。角速度ω＝（θ1＋θ2）／t。圆心角时间函数为θk＝ωΔtk。此处：Δt为时间步长；k＝1／N。

在每个采样周期，按上述规划可得轨迹点对应的圆心角θk。设点Qi为圆弧Q1Q2Q3上一点，其对应圆心角为θi，则第i个插补点在P0－X0Y0Z0系中的坐标为

式中：圆弧Q1Q2Q3在P0－X0Y0Z0坐标系中逆时针时ρ＝1，顺时针时ρ＝－1。

由式（10）、（11）可知：插补点在O－XYZ系中的坐标Pi（xi，yi，zi）满足

2.2 姿态插补

姿态插补采用均匀插补。位置插补中，已算得圆弧运动的总步数N，根据初始和期望姿态，可求得初始和结束时的欧拉角α1，β1，γ1和α2，β2，γ2，并平均分配在N步中。若角度以弧度表示，该返回值在－π～π之间（不包括－π），且在该范围内角度值唯一。

经计算，初始位置的欧拉角为

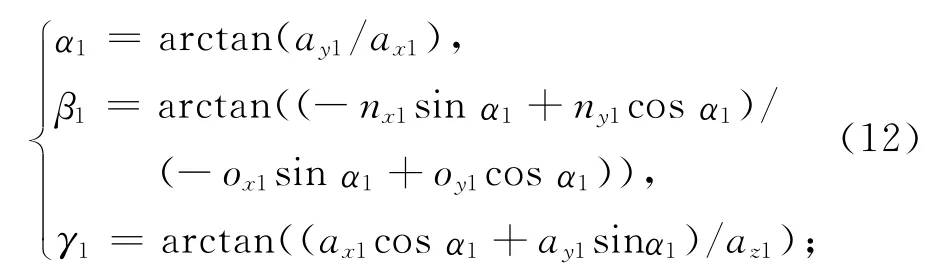
期望位置的欧拉角为

则，第i步的欧拉角为

由此，可得第i步时的姿态阵

式中：a11＝cosαicosβicosγi－sinαisinγi；a12＝－cosαisinβicosγi－sinαicosβi；a13＝cosαisinβi；a21＝sinαicosβicosγl＋cosαisinβi；a22＝－sinαisinβicosγi＋cosαicosβi；a23＝sinαisinγi；a31＝－cosβisinγi；a32＝sinβisinγi；a33＝cosαi。

这样，就获得了每个插补周期内机械臂末端的姿态阵。联合位置规划结果，由运动学反解可求得各关节值送下位机伺服。

3 圆弧轨迹规划仿真

运动学反解中，对同一位姿阵，存在多组解。本文中，从第一关节角开始，各关节角的选取原则为与初始关节角之差的绝对值最小，6关节初始位置均按0°计算。

设实验数据中：起始和终点位姿阵分别为

中间点位置P2为（700，800，400）；末端速度v＝50，T＝0.5s。由过曲线轨迹规划和轨迹姿态插补可得机械手末端起点和机械手末端终点间的运动轨迹如图5所示，差补所得轨迹上的离散点坐标见表2。

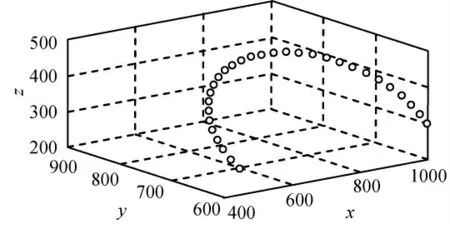
图5 空间中规划的末端三维轨迹Fig.5 Track of robot’s tip

表2 空间圆弧轨迹上的插值点坐标Tab.2 ？？？of space arc track

在此组数据中，解算出的各关节的角度序列如下：

a）关 节1：0.862 17，0.874 65，0.884 19，0.890 74，0.894 29，0.894 91，0.892 72，0.887 86，0.880 52，0.870 89，0.859 20，0.845 68，0.830 56，0.814 09，0.796 50，0.778 02，0.758 90，0.739 35，0.719 60，0.699 83，0.680 26，0.661 07，0.642 43，0.624 52，0.607 48，0.591 46，0.576 62，0.563 08，0.550 97，0.540 42。

b）关 节2：－0.776 84，－0.795 52，－0.813 87，－0.831 53，－0.848 14，－0.863 45，－0.877 20，－0.889 25，－0.899 45，－0.907 74，－0.914 10，－0.918 51，－0.921 04，－0.921 73，－0.920 68，－0.917 98，－0.913 77，－0.908 15，－0.901 26，－0.893 24，－0.884 21，－0.874 32，－0.863 69，－0.852 44，－0.840 69，－0.828 56，－0.816 13，－0.803 51，－0.790 79，－0.778 05。

c）关节3：2.129 5，2.117 7，2.103 6，2.087 4，2.069 5，2.050 1，2.029 5，2.007 9，1.985 8，1.963 4，1.940 9，1.918 8，1.897 1，1.876 4，1.856 6，1.838 2，1.821 3，1.806 1，1.792 9，1.781 7，1.772 7，1.765 9，1.761 6，1.759 7，1.760 3，1.763 3，1.768 7，1.776 5，1.786 5，1.798 6。

d）关 节4：－2.414 7，－2.375 6，－2.333 7，－2.289 7，－2.244 1，－2.197 5，－2.150 6，－2.103 8，－2.057 6，－2.012 6，－1.969 2，－1.927 7，－1.888 6，－1.852 2，－1.818 7，－1.788 3，－1.761 2，－1.737 7，－1.717 6，－1.701 2，－1.688 4，－1.679 3，－1.673 7，－1.671 5，－1.672 7，－1.677 2，－1.684 6，－1.694 9，－1.707 7，－1.722 9。

e）关 节5：－2.296 6，－2.306 8，－2.311 1，－2.309 4，－2.301 8，－2.288 7，－2.270 5，－2.247 7，－2.221 1，－2.191 3，－2.159 1，－2.125 0，－2.089 8，－2.053 9，－2.017 6，－1.981 4，－1.945 4，－1.909 6，－1.874 1，－1.838 8，－1.803 7，－1.768 5，－1.733 0，－1.697 1，－1.660 3，－1.622 4，－1.583 0，－1.541 6，－1.497 7，－1.450 6。

f）关 节6：0.875 94，0.872 86，0.870 15，0.867 93，0.866 33，0.865 42，0.865 26，0.865 89，0.867 31，0.869 51，0.872 45，0.876 09，0.880 34，0.885 14，0.890 39，0.895 99，0.901 82，0.907 78，0.913 75，0.919 61，0.925 23，0.930 50，0.935 29，0.939 47，0.942 93，0.945 52，0.947 12，0.947 61，0.946 84，0.944 69。

圆弧运动各关节的角度变化如图6所示。

图6 圆弧运动各关节的角度变化Fig.6 Angle change of joints when robot moving following a circle

由图5、6可知：用本文中的控制方法，机械臂末端进行点到点圆弧运动时，运动轨迹平滑，分解到各关节，各关节的角度变化平缓，不存在突变，保证了运动的稳定性。

4 结论

本文对空间6R机械臂圆弧轨迹规划方法进行了研究。该插补方法可控制插补精度，如减小末端运动速度和插差值时间间隔，插值点就会更密集，运动轨迹会更接近于圆，关节角变化也会更平缓。因此，应用时需在精度与运动速度间寻找平衡点。该轨迹规划方法可用统一的实时插补递推公式，使用方便，不仅可用于机械臂的圆弧轨迹规划，而且可用于需空间圆弧功能的数控机床系统。此轨迹规划方法满足机械臂点到点圆弧运动的要求，使机械臂能更灵活地抓取物体，或当机械臂在执行点到点运动遇到障碍物时，如障碍物的大概位置、尺寸已知时，可使机械臂末端经过指定空间中的第三点到达目标位置，从而有效避开障碍物。此方法还可用于需精确跟踪圆弧轨迹的场合。

［1］吴镇炜，谈大龙.机械手空间圆弧运动的一种有效轨迹规划方法［J］.机器人，1999（1）：9－12，46.

［2］尼库B（美）.机器人学导论——分析、系统及应用［M］.孙富春，等（译）.北京：电子工业出版社，2004.

［3］张 凯，刘成良，付 庄，等.6R机器人轨迹规划及其在焊接中的应用［J］.机械设计，2002，19（10）：20－23.