用于各向异性媒质的TLM算法

夏新仁，张国华，金贤龙，谢 辉

（空军驻合肥地区军事代表室，安徽 合肥 230000）

0 引言

近年来，各向异性媒质的电磁问题受到关注，出现大量用于处理各向异性媒质的算法，特别是用于处理各向异性媒质的改进FDTD算法。1990年，LUEBBERS提出一种用离散卷积处理色散媒质的RC－FDTD算法，并将此算法推广到各向异性的磁化等离子体，处理各向异性的磁化铁氧体及手征媒质［1－3］。1996年，KELLEY采用电场的分段线性近似——PLRC－FDTD改善了RC－FDTD算法的计算精度［4］。处理各向异性媒质的FDTD方法还有JEC法、DI法、分段线性电流密度递归卷积（PLJERC）法、ADE法等［5－8］。由于整个网格区间的离散化使所需的网格数巨大，尽管FDTD的计算复杂度相对较低，但所需的存储时间和CPU时间仍较长。

TLM算法是一种用于处理电磁问题的全新时域数值方法，该方法功能强大且计算精度高。2002年，YAICH运用TLM算法结合HSCN技术处理磁化等离子体的电磁问题，并扩展至磁化铁氧体［9－10］。本文在Z变换中引入TLM算法，对各向异性媒质的电磁性质计算进行了研究，并与解析法结果进行了对比［11］。

1 各向异性媒质的TLM算法

对一般各向异性媒质，麦克斯韦方程可写成

设电流密度和磁流密度为零，一般各向异性媒质的本构关系为

式中：H为磁场强度；E为电场强度；ε0为自由空间介电常数；μ0为真空磁导率；“＊”为时域卷积；，分别为电极化率和磁化率张量，两者均为3×3维张量的时间函数。本文研究一般各向异性媒质，非双各向异性媒质，故式（2）中的耦合项为零。

将式（2）代入式（1），可得

假设电磁波沿x向传播，以一维电磁问题为例，在电磁波传播的x方向无场分量，y、z向存在相互耦合的电磁场分量，场分量空间节点如图1所示［12］。

图1 一维各向异性媒质的TLM节点Fig.1 TLM node of one－dimensional isomerism medium

场分量空间节点为一个边长为Δl的立方体，4个场分量Ey，Ez，Hy，Hz设置在节点中心，连接相邻节点的端口为V4，V5，V10，V11，端口编号与三维空间一致。因此，在一维空间，电磁波沿x向传播，式（3）可转化为

式中：s为∂／∂t转变Laplace域生成；（▽×H）y为▽×H的y方向分量，其余旋度运算下标符号意义相同。电、磁极化率张量可表示为

将式（4）用场等效电路参数表示，可得

将式（6）变换成行波的形式为

此处，上标“i”为入射波量［11］。定义式（7）左边为外部激励，则

定义传输矩阵t＝2（2I＋sΔtM）－1，则式（9）转化为

对式（9），用双线性Z变换可得离散时域，其中sΔt对应到Z域为

由部分分式展开可得

式中：M2为z的函数；M0，M1为常数张量。

将式（12）代入式（9），整理可得

式中：T－1＝2I＋2M0；κ＝－2I－2M1。

式（13）可简化为

式中：S＝2Fe＋κF－2M2（z）F。

Z域中的z－1在时域对应为一个时延算子，式（14）转变到时域可得

对一般媒质，传输矩阵t因媒质的频率特性不同而改变。用迭代过程计算反射端口电压，即下一个时间步长邻近节点的端口电压，即

对一维各向异性媒质的TLM节点，传播速度

式中：Δl为TLM空间节点的边长；Δt为时间步长。

对磁化等离子体，若电磁波沿x向传播，且假设背景磁场方向平行于x向，则磁化等离子体的等效相对介电常数张量可表示为

式中：ε1＝1－；ε2＝－；ε3＝1－；j为虚数单位。此处：νc为电子的碰撞频率；ω为电磁波频率；ωp为等离子体频率；ωb为电子回旋频率，且ωb＝eB0／me。其中：B0为背景磁场强度；e，me分别为电子电荷数和质量［12］。

电磁波沿x向传播，电磁场在x向无耦合，则

式 中：χ1＝－；χ2＝－j。

为运用TLM算法，将χ1、χ2由频域变换到Laplace域，由Laplace域可变换到Z域。将χ1变换到Laplace域可得

运用部分分式展开，则式（20）可转化为

式（21）变形可得

同理，将χ2变换到Laplace域可得

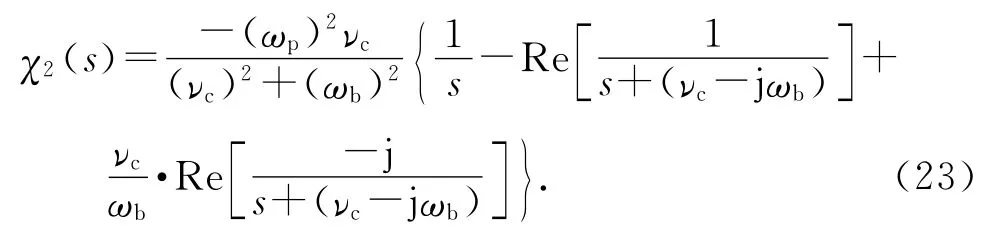
1／s由Laplace域变换到Z域为

用1－z－1乘式（24）右部可得

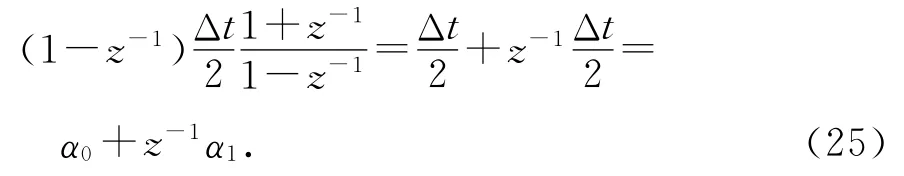
为得到式（12）形式，用1－z－1乘式（27）的右部，并用部分分式展开可得

将θ0、θ1、θ2乘以－j可将变换到Z域。用θ0，θ1，θ2，α0，α1可构建矩阵M0，M1，M2（z）。因此，可得（1－z－1）χ1（s）的Z域形式为

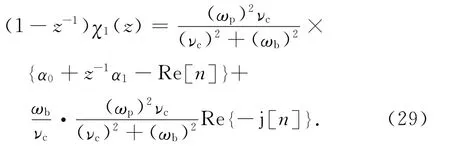
式中：n＝θ0＋z－1（θ1＋θ2）。

式中：m＝－θ1－jB1θ1。

对式（30）进行替代、简化可得

将（1－z－1）χ2（s）变换到Z域形式为

对式（32）进行替代、简化可得

构建矩阵

由式（13）、（14）可知

令M2（z）F＝Se，由M2（z），F可知Se的第一个元素，即Re［Se1］为

将θ2＝代入式（38），整理可得

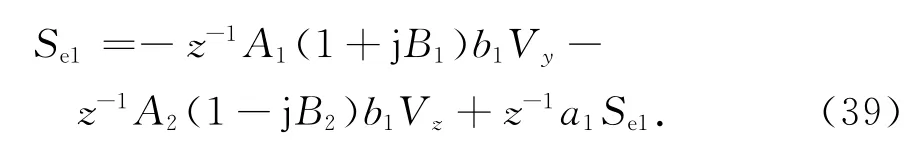
由式（39）可得时域的迭代关系为

同理可得Se的第二个元素，即ℜ［Se2］的时域的迭代关系为

因此，

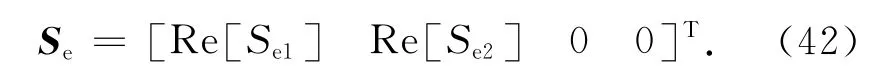
2 仿真

为检验TLM算法在各向异性媒质中的有效性和计算精度，对某一维实例用TLM算法模拟电磁脉冲垂直入射到各向异性磁化等离子体层中的传播。假设电磁波的传播方向和外加磁场的方向平行，等离子体层的两边为自由空间，入射源采用高斯脉冲。TLM计算空间分为500个空间节点元胞，空间节点编号0～300和420～500为真空，等离子体所占的空间节点编号取300～420，空间步长取Δ＝75μm，假设条件稳定，时间步长取Δt＝0.125ps。背景磁场强度B0＝1.7T，等离子体密度n0＝3.1×1019m－3，碰撞频率νc＝20GHz，磁化等离子体层厚度d＝9mm。

电磁波在各向异性磁化等离子体中传播时，其基本模式为左旋圆极化波（LCP）和右旋圆极化波（RCP）。为得到LCP和RCP的反射系数与透射系数的幅度及相位与频率的变化关系，实现过程为：对等离子体层的前后的电场强度值作离散Fourier变换［13］。将电场强度随时间的变化转换到频域，得到电场随频率的变化关系，有

用解析法和TLM算法计算各向异性磁化等离子体层中左、右旋圆极化波的反射系数和透射系数的幅度和相位结果分别如图2～9所示［14］。由图2～9可知：本文结果与解析的结果吻合得较好，表明TLM算法具有高效性和高精度。

图2 右旋极化波反射系数幅值Fig.2 Reflection coefficient magnitude for RCP polarization

图3 右旋极化波反射系数相位Fig.3 Reflection coefficient phase for RCP polarization

图4 左旋极化波反射系数幅值Fig.4 Reflection coefficient magnitude for LCP polarization

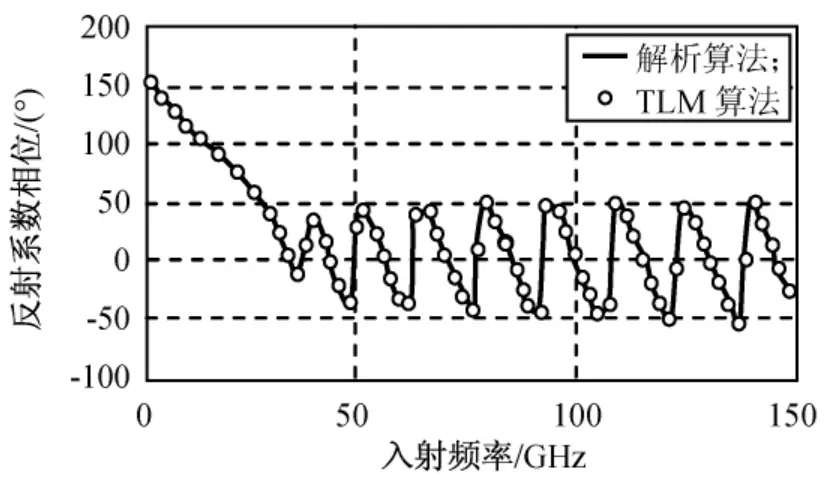
图5 左旋极化波反射系数相位Fig.5 Reflection coefficient phase for LCP polarization

图6 右旋极化波透射系数幅值Fig.6 Transmission coefficient magnitude for RCP polarization

图7 右旋极化波透射系数相位Fig.7 Transmission coefficient phase for RCP polarization

图8 左旋极化波透射系数幅值Fig.8 Transmission coefficient magnitude for LCP polarization

3 结束语

本文提出了一种用于各向异性媒质的全新时域数值方法。该法可对各向异性媒质进行建模，也可用于各向异性媒质中波的传播和散射分析。方法通过Z变换由频域变换到Z域，避免了时域的卷积运算，保证了计算的高效率。用本文方法计算了磁化等离子体平板对平行于磁场传播的电磁波的反射和透射系数幅度和相位，并与解析解的结果进行比对，两种方法吻合较好，验证了方法的高效性和高精度性。

图9 左旋极化波透射系数相位Fig.9 Transmission coefficient phase for LCP polarization

［1］LUEBBERS R，HUNSBERGER F P，KUNZ K S，et al.A frequency－dependent finite－difference time－domain formulation for dispersive materials［J］.Transactions on Electromagnetic Compatibility，1990，32（3）：222－227.

［2］HUNSBERGER F，LUEBBERS R，KUNZ K.Finite－difference time－domain analysis of gyrotropic media magnetized plasma［J］.Transactions on Antennas and Propagation，1992，40（12）：1489－1495.

［3］HUNSBERGER F P.Extension of the finite－difference time－domain method to gyrotropic media［D］.Nittany Valley：The Pennsylvania State University，1991.

［4］KELLEY D，LUEBBERS R J.Piecewise linear recursive convolution for dispersive media using FDTD［J］.Transactions on Antennas and Propagation，1996，44（6）：792－797.

［5］XU L J，YUAN N C.JEC－FDTD for 2－D conducting cylinder coated by anisotropic magnetized plasma［J］.IEEE Microwave and Wireless Components Letters，2005，15（12）：892－894.

［6］刘少斌，莫锦军，袁乃昌.各向异性磁化等离子体的JEC－FDTD算法［J］.物理学报，2004，53（3）：783－787.

［7］LIU S B，MO J J，YUAN N C.Piecewise linear current density recursive convolution FDTD implementation for anisotropic magnetized plasmas［J］.Microwave and Wireless Components Letters，2004，14（5）：222－224.

［8］刘少斌，莫锦军，袁乃昌.各向异性磁化等离子体的辅助方程FDTD算法［J］.物理学报，2004，53（7）：2233－2236.

［9］YAICH M I，KHALLADI M，ZEKIK I，etal.Modeling of frequency－dependent magnetized plasma in hybrid symmetrical condensed TLM method［J］.Microwave and Wireless Components Letters，2002，12（8）：293－295.

［10］YAICH M I，KHALLADI M.A SCN－TLM model for the analysis of ferrite media［J］.Microwave and Wireless Components Letters，2003，13（6）：217－219.

［11］LIU S，ZHONG S Y，LIU S B.Piecewise linear recursive convolution FDTD method for magnetized plasma［J］.Journal of Systems Engineering and Electronics，2006，17（2）：290－295.

［12］FURSE C M，GANDHI O P.Why the DFT is faster than the FFT for FDTD time－to－frequency domain conversions［J］.IEEE Microwave Guided Wave Letter，1995，9（5）：326－328.

［13］袁敬闳，莫怀德.等离子体中的波［M］.成都：电子科技大学出版社，1990.