两种南北位置保持控制策略研究

黄霄腾，张文雅，何伟平

（中国人民解放军63999部队，北京 100094）

0 引言

由于日、月引力和地球非球形摄动的影响，三轴稳定地球同步卫星轨道倾角和升交点赤经会不断变化，每年倾角矢量漂移率的变化为0.75°～0.95°［1］。为使卫星的南北位置误差保持在规定的范围内，必须定期实施南北位置保持（轨道倾角控制）。卫星的南北位置保持是在轨运行时最复杂的测控工作，在燃料量和倾角保持精度要求一定的前提下，选择目标轨道倾角，使卫星两次控制时间间隔最长，且消耗燃料最省是南北保持控制的关键。根据某三轴稳定地球同步卫星7年寿命期内的倾角变化，本文对其南北位置保持的短期策略和长期策略进行了研究。

1 倾角漂移原理

卫星倾角的漂移是太阳、月球摄动和地球非球形摄动引起的，其结果是使倾角矢量倒向春分点方向［2］。其中太阳谐动引起半年为周期的波动，月球摄动引起两星期为周期的较小波动，它们是倾角变化的主要因素。

1.1 太阳摄动

因静止卫星的轨道基本位于赤道面，与太阳视运动轨道的几何关系较为固定。设卫星轨道倾角为零，赤经为α，则太阳摄动法向引力

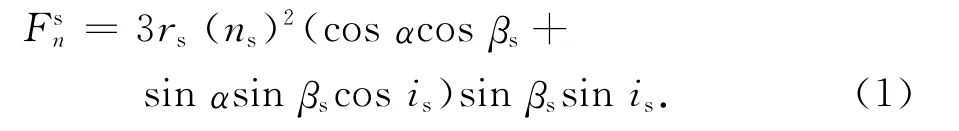
式中：rs为地球同步圆轨道半径；ns为太阳视运动的平均转速；βs，is分别为太阳视运动的黄经和黄道倾角。

当βs＝±90°即在夏至或冬至时，太阳处于赤道坐标的YZ平面。则式（1）可简化为

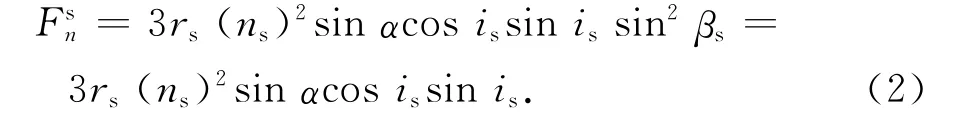
由式（2）可知：在赤经0°～180°的半圈内，卫星受北向引力；在赤经180°～360°的半圈内，卫星受南向引力，由此产生平均速率为每年0.27°的漂移［2］。春秋分日法向引力为零。

1.2 月球摄动

月球引力作用的基本规律与太阳引力作用类同。但在18.6年的周期中，月球轨道与赤道的夹角在23.45°±5.14°范围内变化，受力大小的变化使倾角矢量每年产生0.48°～0.68°的漂移［1］。

卫星轨道倾角矢量i的总漂移是太阳和月球摄动的影响总和，每年漂移率的变化为0.75°～0.95°，方向随月球轨道极的变化而变化，有

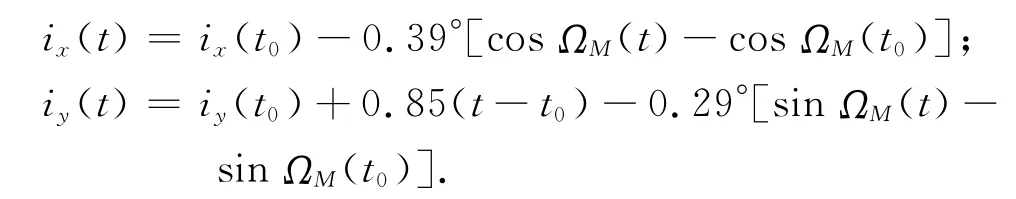
式中：ΩM为月球白道升交点的黄经；t0为初始历元时间；ix，iy为i的分量。

除太阳和月球摄动外，另外须考虑地球非球形摄动对轨道倾角影响产生的每年－0.005°的漂移，三者的综合影响可以平均近似地表示为倾角矢量绕坐标为（0，－7.4°）的极以54年为周期作负方向旋转。

实际上，倾角漂移与初始位置关系不大，不同频率的倾角机动，其位置保持的总速度增量几乎相同。2009～2016年的倾角矢量历年变化，以及克服倾角漂移所需的速度增量见表1。7年内的卫星倾角矢量漂移如图1所示，漂移方向近似指向iy轴向。

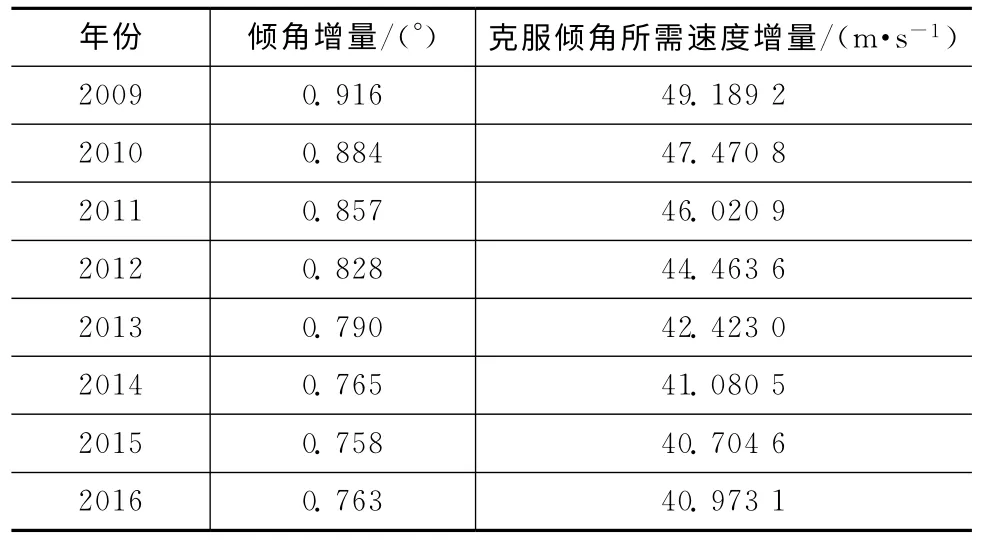
表1 2009～2016年卫星克服倾角漂移所需的速度增量Tab.1 Velocity increment to kill inclination evolution from 2009～2016

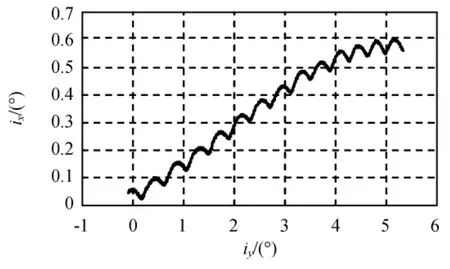
图1 7年内倾角矢量漂移Fig.1 Inclination vector evolution during seven years

2 南北位置保持策略

实际任务中，可认为倾角漂移与卫星的经度及经度机动无关，此时可单独制定倾角机动策略。通常，倾角位置保持的方法是让倾角自由漂移，到达保持环边界时执行机动，将倾角向反方向控制至保持环负边界（如图2所示），在任务寿命期内使倾角矢量始终在保持环内，且地面控制次数最少。由历年倾角矢量漂移量可知：当保持环半径为0.1°时，每年约需进行4～5次倾角机动。因此，倾角机动方向选择是南北控制的关键，可根据任务需要，综合星上燃料及卫星寿命时间确定倾角机动控制采用短期策略或长期策略。

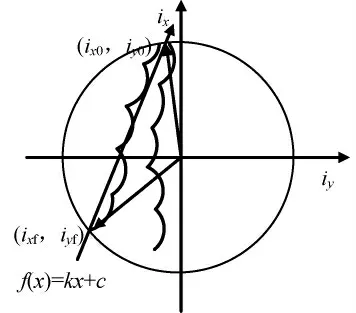
图2 目标倾角示意Fig.2 Target inclination

2.1 倾角控制短期策略

一般两次倾角机动的时间间隔为2～3月，为使保持间隔时间最长，采用倾角控制短期策略方法。考虑倾角长期漂移方向近似沿iy轴向，可对3月轨道预报中的轨道倾角变化进行线性拟合，拟合曲线方程为f（x）＝kx＋c，则负的曲线斜率即为短期控制的最优方向。如图3所示，控制前后轨道倾角矢量分别为［ix0iy0］，［ixfiyf］，解方程组

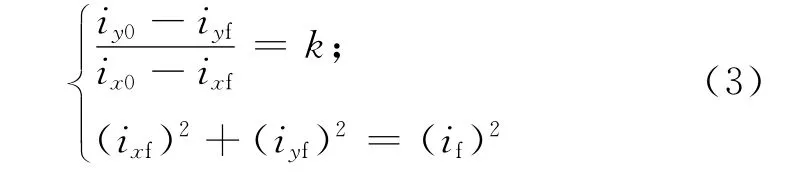
即可求得目标倾角矢量，再求得目标轨道升交点赤经Ωf＝arctan（iyf／ixf）。

2.2 倾角控制长期策略

卫星受日月摄动作用，在整个任务寿命期内，为使倾角矢量始终保持在精度范围内，须进行一系列机动控制。设寿命期内总共进行南北控制N次，每次机动的倾角控制量和控制时间分别为Δij，tj，j＝1，2，…，N，长期策略的目的就是到任务结束（t＝T）时刻，满足∀t≤T，

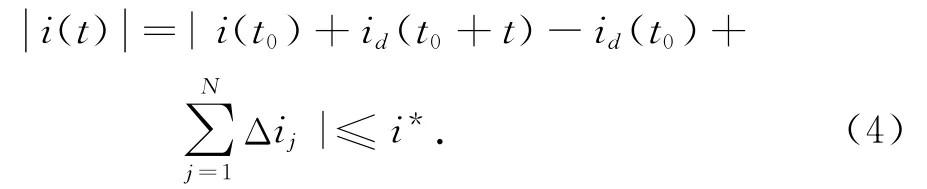
式中：id（t）为摄动引起的倾角矢量随时间的变化。当N次机动的倾角控制量达到最小，即Fmin＝时，燃料最优，即最优解是满足漂移曲线上的每点均在圆心为－Δij（tj＜t，j＝1，2，…，N）、半径为i＊的一组圆的包络线内［3］。

倾角控制最优解的简化模型如图3所示。当星上燃料一定时，为使倾角矢量维持在要求的精度范围内的时间最长，需使目标倾角在保持圆上，且升交点赤经满足方程组

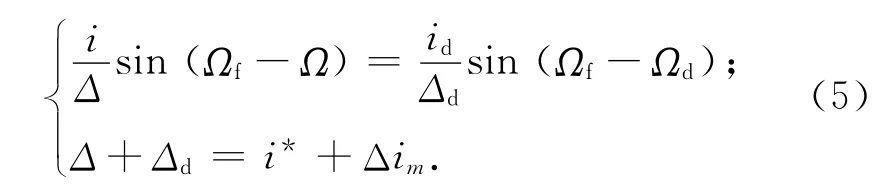
式中：i，Ω分别为控前轨道倾角和升交点赤经；id，Ωd为矢量id（t0＋T）－id（t0）的极坐标分量；t0为倾角控制时刻；T为最长保持时间；i＊为保持精度；Δim为最大倾角修正能力；

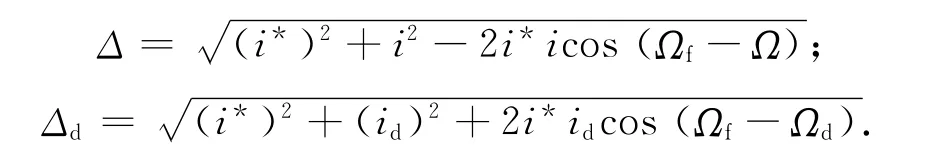
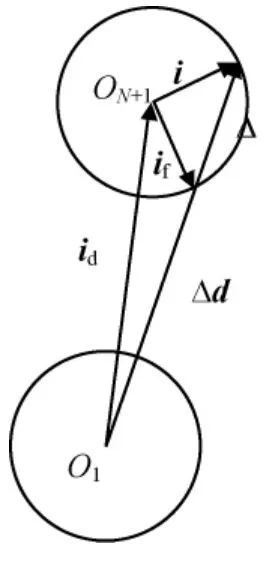
图3 倾角控制示意Fig.3 Control of inclination

适当选择求解方程组的门限，以保证方程组有唯一解Ωf或无解。若无解，则按燃料最省原则选取目标倾角和升交点赤经。

3 仿真

设2008年底开始对倾角初始位置为i＝0.1°，Ω＝52°的地球同步卫星进行第一次南北位置保持控制，卫星寿命期为7年。整个寿命期内南北方向控制精度为±0.1°。每次控制效率均为100%，不考虑东西方向耦合误差，分别采用倾角控制长期策略和短期策略进行南北位置保持控制参数计算。

寿命期内的倾角矢量变化分别如图4、5所示（直线反映倾角控制向），寿命期内的倾角幅值变化分别如图6、7所示。由图可知：两种方法均能保证寿命期内倾角矢量幅值始终控制在0.1°的保持圆内，满足控制精度要求，其中，短期策略倾角控制方向基本沿过坐标系原点直线方向，长期策略倾角控制方向大致沿同一方向。由上述两种方法得到的整个寿命期内历次倾角控制量柱状图分别如图8、9所示。统计结果表明：采用短期策略和长期策略两种方法，理想状况下需进行的机动次数分别为29，30次，倾角控制量分别为5.51°，5.28°。

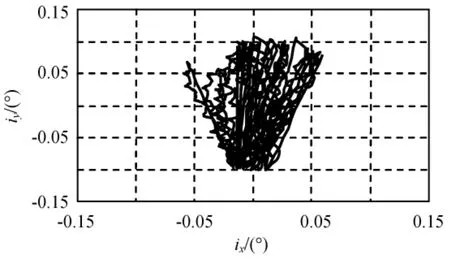
图4 短期策略倾角矢量Fig.4 Inclination vector evolution of short－term strategy

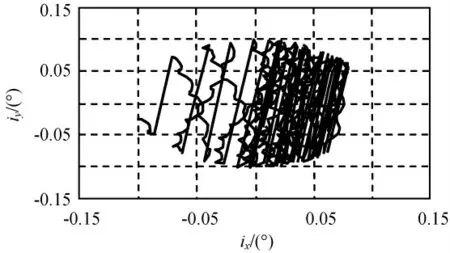
图5 长期策略倾角矢量Fig.5 Inclination vector evolution of long－term strategy

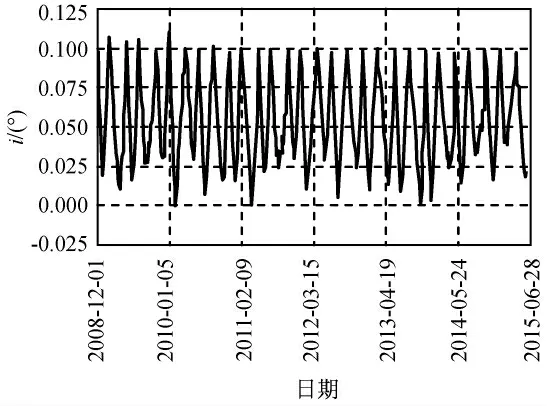
图6 短期策略轨道倾角Fig.6 Inclination evolution of short－term strategy

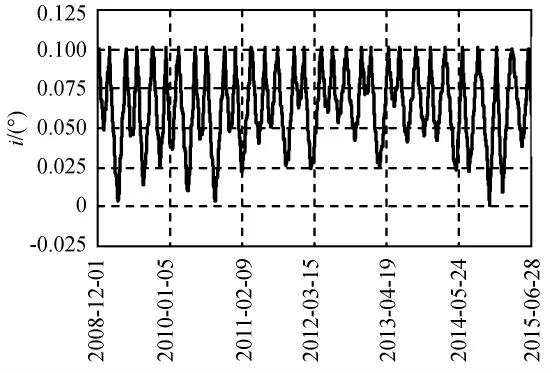
图7 长期策略轨道倾角Fig.7 Inclination evolution of long－term strategy

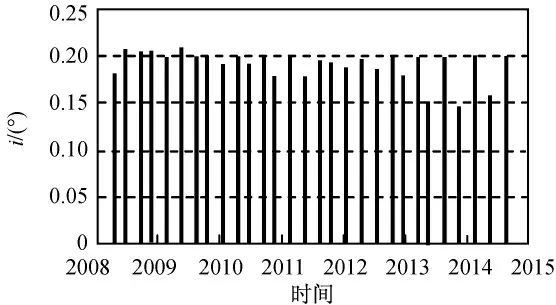
图8 短期策略倾角控制量Fig.8 Inclination controlling quantity of short－term strategy

为获知机动前后倾角向量变化，每次机动时将保持圆向漂移方向移动，使本次控制目标倾角矢量与控前倾角矢量重合，对应的倾角保持机动如图10、11所示。图中折线为保持圆圆心的连线，每段折线的长度反映燃料消耗状况，斜率对应当次保持倾角控制方向。由图10、11可知：采用短期策略控制时，受短周期摄动影响，机动方向呈Z字形，而采用长期策略控制时，历次控制方向基本一致，保持圆圆心折线连成一线，对应图7中的一系列平行直线，对所有圆心进行线性拟合得倾角控制方向斜率约为0.12。同样，对整个寿命期内倾角漂移进行线性拟合得倾角漂移斜率约为0.114 5，按此斜率用式（3）计算目标倾角，保持机动结果如图12所示。

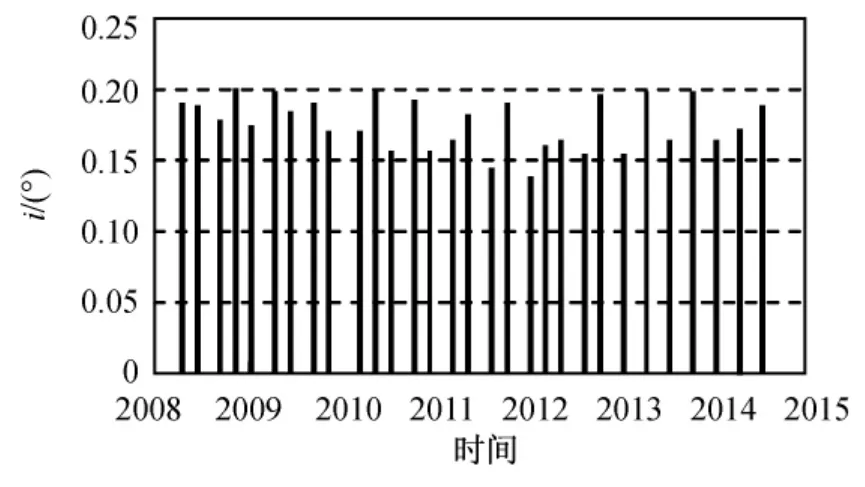
图9 长期策略倾角控制量Fig.9 Inclination controlling quantity of long－term strategy

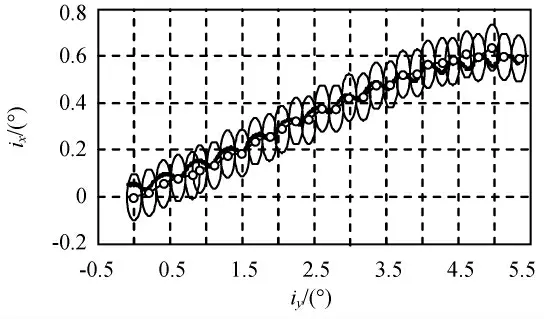
图10 短期策略倾角保持机动Fig.10 Inclination maneuver of short－term strategy

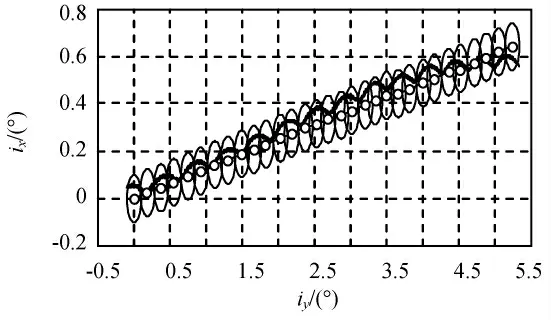
图11 长期策略倾角保持机动Fig.11 Inclination maneuver of long－term strategy

仿真表明：在满足控制精度要求的条件下，两种方法的控制次数基本相当，而长期控制策略因兼顾整个寿命期的倾角漂移而更省燃料，正常情况下可延长卫星寿命2～3月。特殊地，当拟合精度要求不高时，可直接拟合倾角长期漂移方向，取其反方向作为倾角控制的最优方向，在不多消耗燃料的前提下，满足精度要求的同时也简化计算。然而，当控制精度提高，即保持圆半径减小时，该拟合方法不能保证漂移曲线完全位于圆的包络线内。

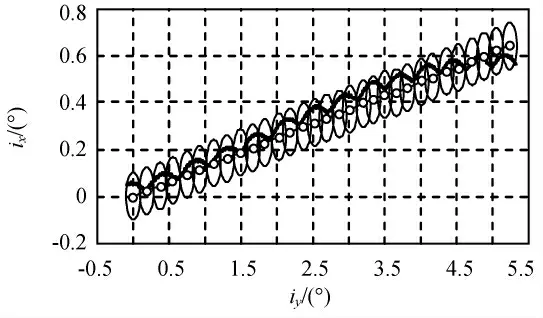
图12 长期策略倾角保持机动Fig.12 Inclination maneuver of long－term strategy by linear fitting

4 结束语

本文对采用倾角控制短期策略和长期策略的南北位置保持方法进行了仿真分析。结果表明：两种南北位置保持策略均能使倾角控制在既定的精度范围内，从长远角度看，短期策略的南北保持周期较长，卫星控制频度略低，而长期策略燃料消耗量更少，计算过程相对复杂。文中分析结果对同类卫星任务前的南北位置保持策略制定有一定的参考意义。

［1］SOOP E M.地球静止轨道手册［M］.王正才，等（译）.北京：国防工业出版社，1999.

［2］章仁为.卫星轨道姿态动力学与控制［M］.北京：北京航空航天大学出版社，1998.

［3］杨嘉摨.卫星系列·航天器轨道动力学与控制（下）［M］.北京：中国宇航出版社，2002.