考虑轨道摄动的外热流计算分析
王宇宁,魏 承,赵 阳
(哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001)
0 引言
作为航天器在轨道空间的主要热源,轨道外热流计算成为航天器热分析与热设计的基础。目前,外热流计算主要有能束均匀分布法、积分法、随机模拟法和蒙特卡洛法等。文献[1]基于兰贝特余弦定律和能量守恒定律,推导了均匀布置能束发射点和发射方向上能束的能量计算公式,但由于实际物体辐射不满足兰贝特定律,其实用性、可扩展性较差。积分法通过球面三角关系求解外热流角系数并积分,不能考虑多曲面间遮挡[2]。文献[3]采用随机模拟法,随机选取地球表面面积元,用球面三角关系计算该面元对空间飞行器表面上任一微元面的地球反照和红外辐射角系数,而后大量选取面元并以累加代替积分,但并未解决遮挡问题。蒙特卡洛法因其通用性、扩展性强,易解决遮挡问题,易与节点网络法结合,而成为外热流计算的主要方法,得到了广泛应用[4-5]。但目前多数文献均使用角系数计算外热流,仅考虑入射外热流被直接吸收部分,未对外热流的多次反射和吸收作深入研究。
在外热流计算中,国外热分析软件忽略了轨道摄动和太阳矢量变化的影响,导致其瞬态外热流计算存在较大误差。如Thermal Desktop软件,在确定入轨参数后只计算初始轨道由平近角或真近角确定的给定位置处的外热流,而计算瞬态温度场时,则反复输入已计算外热流进行迭代。应用热分析软件进行热设计时,一般根据瞬态温度场的计算结果验证热设计的有效性和合理性。因外热流计算不准确,导致瞬态温度场计算存在误差,致使热设计有效性的验证缺乏可靠依据。为弥补目前该领域的不足,便于与节点网络法结合,本文对考虑轨道摄动的外热流计算进行了研究。
1 外热流角系数及辐射传递因子定义
在辐射热传递相关领域中,曲面Ai到曲面Aj的角系数定义为曲面Ai投射到曲面Aj辐射热流量与曲面Ai发出的总辐射热流量之比。温度场数值计算中的节点网络法常用热流量建立热平衡方程,故该曲面间角系数定义方式可很好地与节点网络法结合。
由于轨道外热流的特殊性,太阳、地球总辐射热流量计算不易,传统外热流角系数均定义为外热流密度与外热流强度之比,为无量纲数,不利于辐射传递因子概念的导出以及与节点网络法结合。为此,本文将外热流角系数定义为投射外热流量与外热流强度之比。
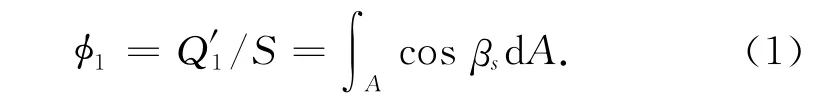
式中:βs为微元面dA外法线与太阳照射方向夹角。
定义地球红外辐射角系数为投射到航天器面元的地球红外辐射外热流量与地球平均红外辐射强度Ei0之比。对航天器面元A,地球红外辐射角系数可表示为
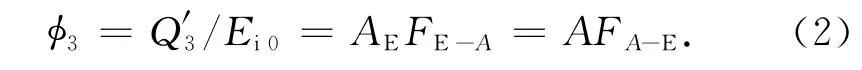
式中:AE为地球表面积;FE-A为地球表面到航天器面元的角系数;FA-E为航天器面元到地球表面角系数。另有
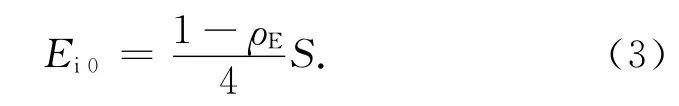
式中:ρE为地球表面平均反射率。地球反照辐射角系数定义为投射到航天器面元的地球反照辐射外热流量与地球平均反照辐射强度Er0之比。对航天器面元A,地球红外辐射角系数可表示为
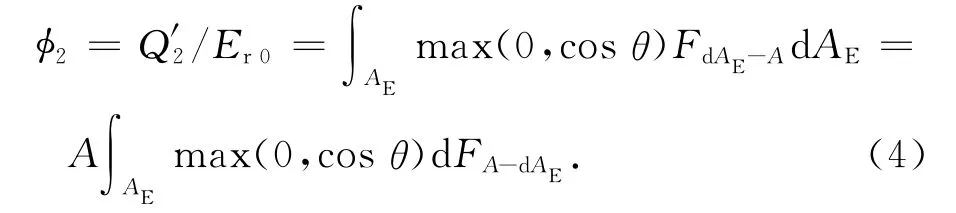
式中:dAE为地球表面任一微元面积;θ为太阳矢量与dAE外法线的夹角;为微元面dAE到航天器面元A的角系数;为A到dAE的角系数。FE-A,FA-E,均为一般意义的辐射换热角系数[6]。Er0=ρsS。
用外热流辐射传递因子可较好地计算考虑多次反射后航天器表面单元(简称面元)吸收外热流,其定义为航天器面元实际吸收外热流量与相应外热流辐射强度之比。根据研究对象不同,又分为太阳辐射传递因子、地球红外辐射传递因子及地球反照辐射传递因子。计算辐射传递因子时,传统蒙特卡洛法需跟踪能束直至其被某面元吸收,效率低。为此,本文结合Gebhart方法(即改进的蒙特卡洛法),先用蒙特卡洛法计算外热流角系数,再根据外热流角系数计算辐射传递因子。算法数据流如图1所示。
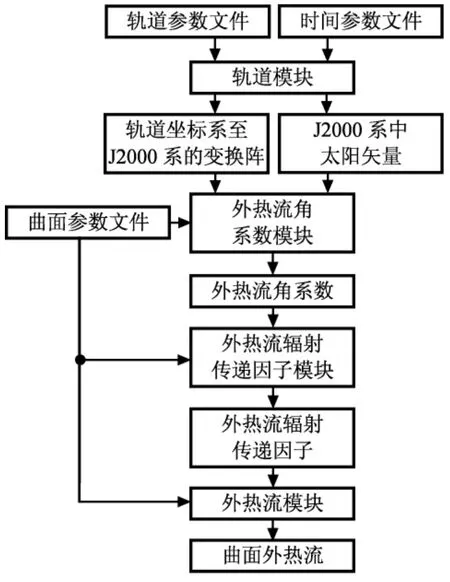
图1 算法数据流Fig.1 Data flowchart of algorithm
2 考虑摄动及太阳矢量变化的外热流算法
2.1 轨道及太阳位置确定
为计算外热流角系数,先须求解太阳、地球及航天器三者位置关系,本文用SGP4轨道模型确定轨道。SGP4摄动轨道模型采用Brower引力场模型和Lane大气密度模型,推导出简化解析式,可用于低轨卫星(轨道周期小于225min,高度低于6 000km)的轨道确定[7-8]。
J2000系中太阳矢量坐标(xs,ys,zs)可表示为
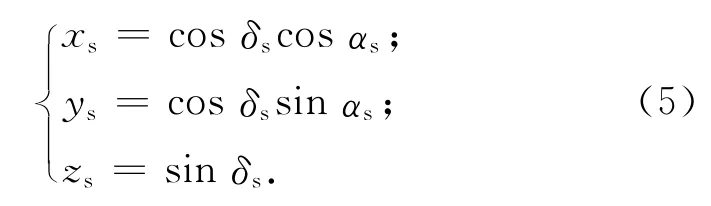
式中:αs,δs分别为太阳赤经和赤纬,且

另有
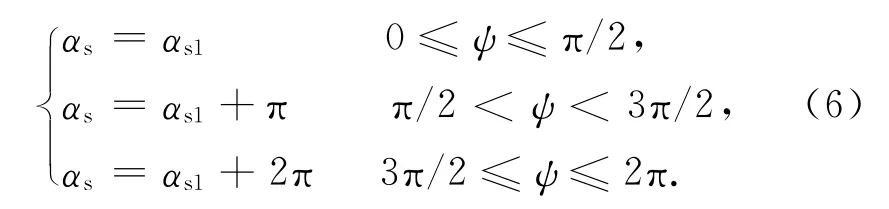
此处:αs1为天球赤道面内由春分点矢量转到太阳矢量在赤道面内的投影角;I为黄赤交角,且I=23.5°;ψ为太阳黄经,且

其中:t为航天器运行时间;为太阳黄经的平均变化率,且=7.168×10-4rad/h;ψ0为太阳黄经初值,且
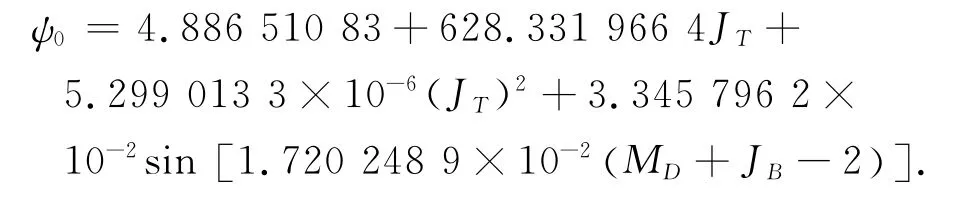
这里:JT为自2000年儒略年首算起的儒略世纪数;MD为从1月0日至卫星发射月份的儒略日;JB为卫星发射日期所在月份的日数[2、9]。
轨道确定后,先由J2000系中航天器的位置、速度矢量确定J2000系至轨道坐标系的坐标变换阵。为便于计算,选择轨道坐标系为蒙特卡洛法的系统坐标系。
传统方法通过求解地影椭圆方程判断航天器是否处于地球阴影区,计算繁琐[2]。考虑轨道摄动和太阳矢量变化后,地影椭圆实时变化,传统方法不再适用。由于已知J2000系中航天器位置矢量和太阳矢量,本文用文献[10]的矢量方法解算。
2.2 外热流角系数计算
用蒙特卡洛法计算太阳辐射角系数时,传统方法利用假定平面模拟太阳照射方向,以此平面到航天器面元的角系数替代太阳辐射角系数[4]。该法需保证假定平面的面积,通用性较差,无法估计假定平面形状及其到航天器面元距离对计算产生的影响。对此,本文提出改进方法:由航天器面元发射概率模型随机产生发射点,以太阳矢量为发射方向确定能束;根据精度要求确定大量能束,判断能束是否被其他面元遮挡;由未被遮挡能束发射点处法线矢量与太阳矢量夹角余弦与总能束数之比得到太阳辐射角系数。如将航天器划分为面元N个,每个面元发射能束Nr条,其中某面元(面积Ai)在某轨道位置处的太阳辐射角系数φ1i计算流程如图2所示。
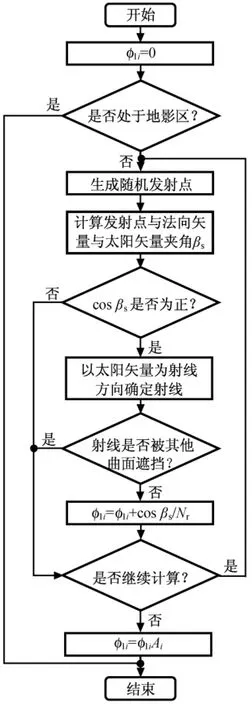
图2 太阳辐射角系数计算流程Fig.2 Flowchart of solar radiation view factor algorithm
文献[5]对应用蒙特卡洛法计算地球红外辐射角系数和反照辐射角系数进行了研究。由于两者计算时均需通过航天器面元能束发射概率模型生成能束,并判断能束是否被其他面元遮挡及是否到达地球表面,如单独计算,耗时较长,而文献[5]未对此提出改进方案。为提高计算效率,本文对该法作如下改进:用一次循环同时计算面元Ai地球红外辐射角系数φ3i和反照辐射角系数φ2i,方法流程如图3所示。
2.3 外热流辐射传递因子计算
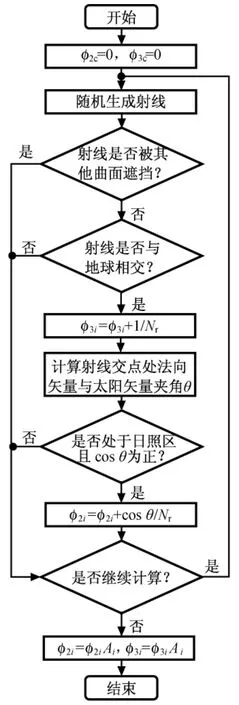
图3 地球红外及反照辐射角系数计算流程Fig.3 Flowchart of earth infrared and reflected radiation view factor algorithm
根据Gebhart方法,航天器面元吸收的外热流包含直接吸收和经其他面元反射后吸收两部分。由表面间辐射传递因子定义,航天器面元Ai吸收的外热流
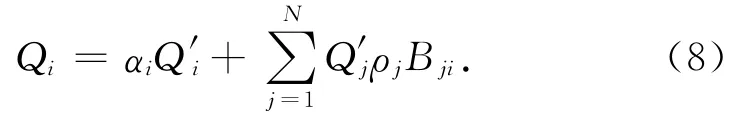
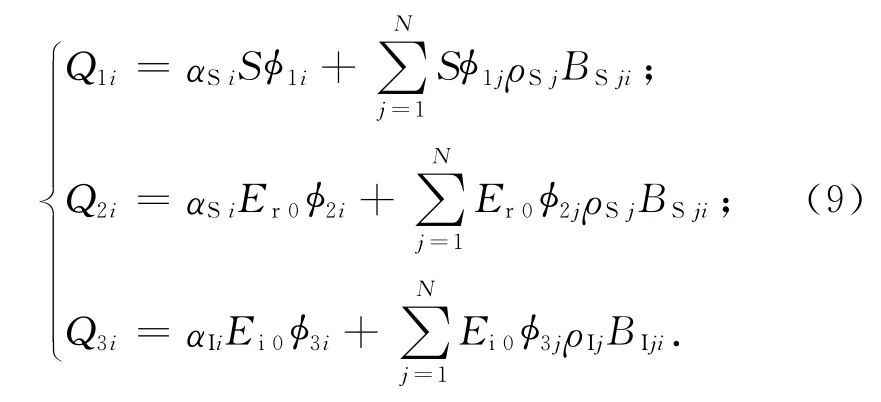
式中:Q1i,Q2i,Q3i分别为面元Ai吸收的太阳辐射、地球反照辐射和地球红外辐射外热流;αSi分别为面元Ai在太阳辐射光谱下的吸收率;ρSj为面元Aj在太阳辐射光谱下的反射率;BSji为太阳辐射光谱下的面元Aj到面元Ai的辐射传递因子;αIi为面元Ai在红外辐射光谱下的吸收率;ρIj为面元Aj在红外辐射光谱下的反射率;BIji为红外辐射光谱下的面元Aj到面元Ai的辐射传递因子。由外热流辐射传递因子定义,有
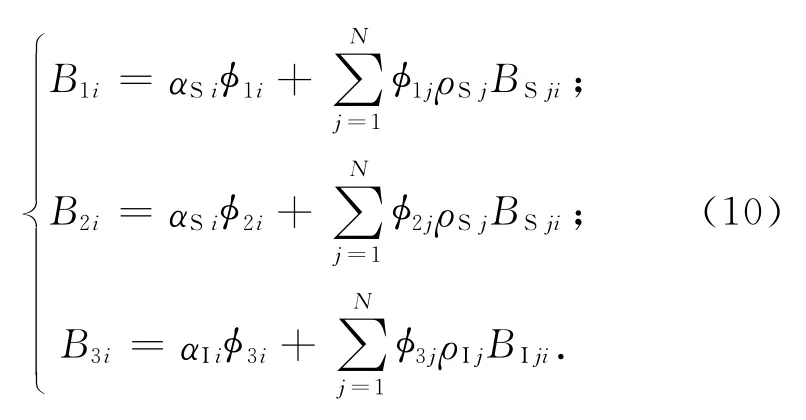
式中:B1i,B2i,B3i分别为面元Ai的太阳辐射、地球反照辐射和地球红外辐射传递因子。计算轨道外热流时,先求得各面元外热流角系数,再由式(10)计算各面元外热流辐射传递因子,最后根据辐射因子定义计算外热流。
3 仿真分析
本文以相互遮挡的一圆环面和一个三角形面(分别如图4、5所示)进行轨道外热流计算,并与商业软件Thermal Desktop对照,分析太阳矢量变化及轨道摄动对外热流计算的影响。设曲面姿态为对地三轴稳定时,轨道坐标系中三角形面三顶点坐标分别为(0,0,0),(1.5,1.5,0),(2,0,0);圆环面圆心坐标为(0,0,1);顶角60°;内外半径分别为1,2m;面元红外光谱发射率均为0.9;太阳光谱吸收率均为0.7。取入轨点轨道参数为轨道倾角30°,轨道周期5 400s,偏心率0.009,升交点赤经90°,近地点角距270°,平近角0°,入轨时刻2009-01-01零时整。
因三角形面-Z侧只受太阳辐射外热流作用,圆环面+Z侧仅受地球红外、反照辐射外热流作用,相互间不存在遮挡和反射关系,因此对其计算结果不作明确说明。
3.1 摄动及太阳矢量变化对外热流影响
Thermal Desktop软件根据入轨点参数确定轨道位置,不考虑轨道摄动和太阳矢量变化的影响,因此其轨道外热流在各轨道周期中随轨道位置变化,为时间的周期函数。使用外热流辐射传递因子计算入轨后、1d后、7d后及30d后1个轨道周期内圆环面背地侧(Z轴负向)外热流变化趋势如图6~9所示。
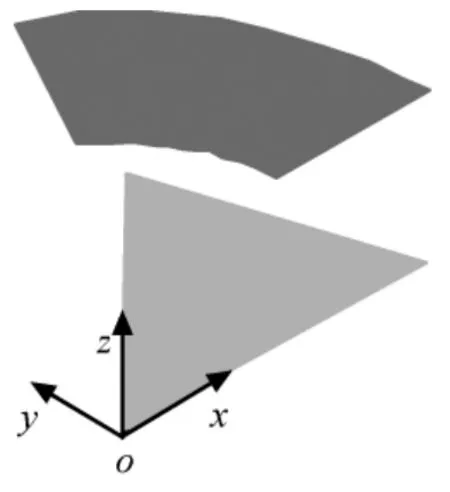
图4 西南等轴视图Fig.4 Southwest view
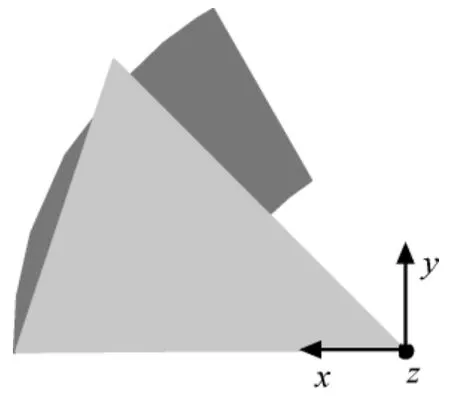
图5 仰视图Fig.5 Upward view
由图6~9可知:在第1周期(90min)内,由式(7)可得太阳黄经变化约0.06°;由式(5)、(6)所得太阳矢量变化极小,短时间内轨道摄动的影响亦可忽略,Thermal Desktop商业软件为NASA推广,不考虑太阳矢量变化和摄动影响时,其计算精度可有效保证,此时本文算法计算结果与其良好吻合,验证了本文算法体系的正确性;1d后,Thermal Desktop软件与本文算法的外热流变化趋势一致,但已开始偏离,同时太阳矢量变化对外热流影响较小;7d后,地球阴影区所对应的平近角变化大于30°,Thermal Desktop软件已完全不能反映外热流应有的变化趋势,同时太阳矢量变化也开始影响外热流计算精度,但并不明显;30d后,太阳矢量变化导致地影区对应的平近角变化大于60°,但未影响外热流变化趋势。

图6 入轨后1个周期外热流变化Fig.6 Periodic variation of external heat flux after epoch
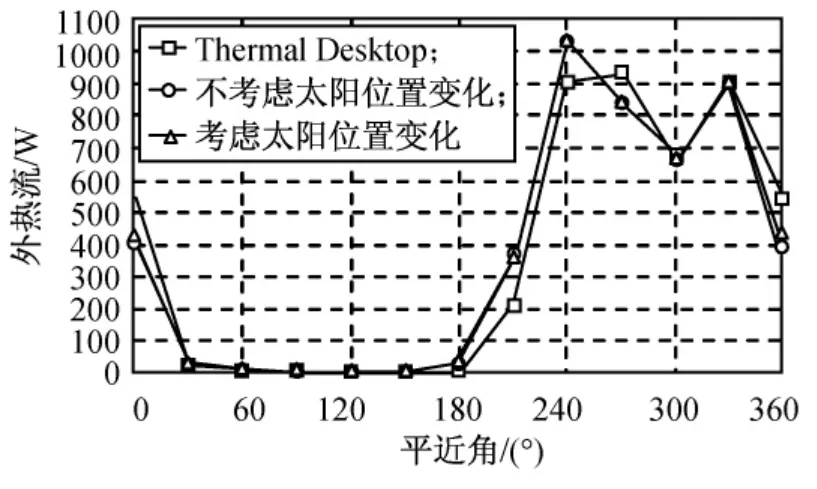
图7 1d后1个周期内外热流变化Fig.7 Periodic Variation of external heat flux after a day

图8 7d后1个内外热流变化Fig.8 Periodic variation of external heat flux after 7d
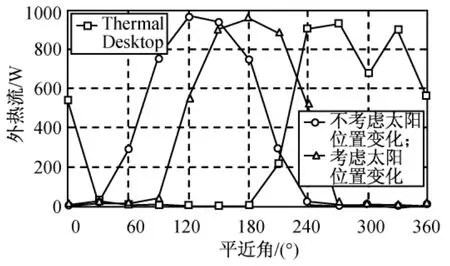
图9 30d后1个周期内外热流变化Fig.9 Periodic variation of external heat flux after 30d
当轨道倾角为80°时,考虑外热流辐射传递因子的7,30d后1周期内外热流变化分别如图10、11所示。
由图10、11可知:当轨道倾角为80°时,7d后,太阳矢量变化对地影区位置影响较小,并未影响外热流变化趋势,而外热流峰值受到一定影响;30d后,太阳矢量变化导致地球阴影区所对应的平近角变化大于30°,同时外热流变化趋势及峰值也产生明显变化。
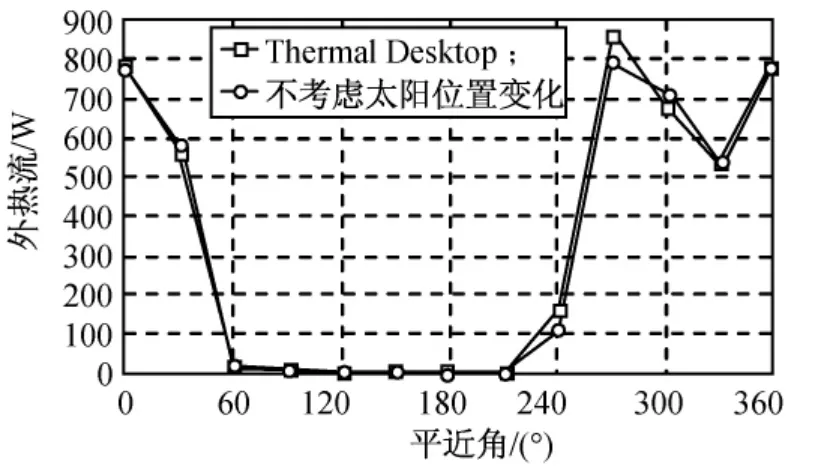
图10 7d后1个周期内外热流变化Fig.10 Periodic variation of external heat flux after 7d
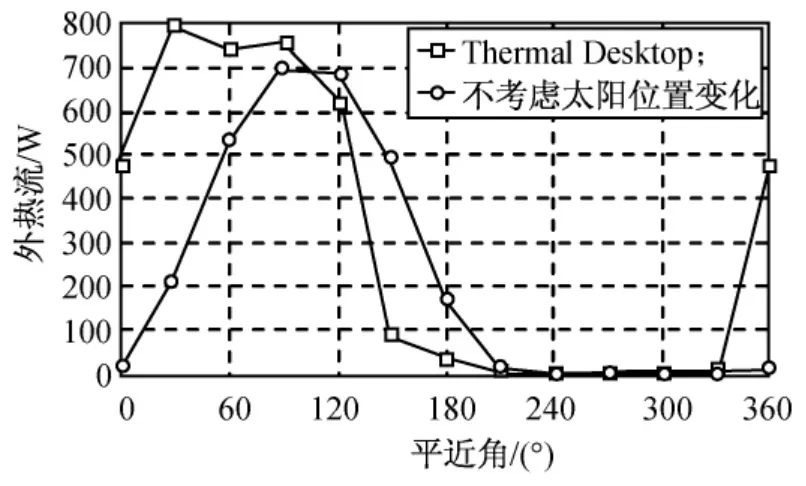
图11 30d后1个周期内外热流变化Fig.11 Periodic variation of external heat flux after 30d
3.2 多次反射对外热流影响
用外热流角系数和外热流辐射传递因子计算入轨后1个周期内三角形面+Z侧和圆环面-Z侧外热流,结果分别如图12、13所示。
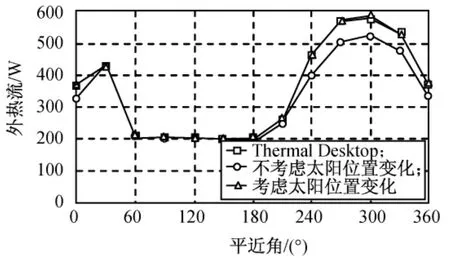
图12 三角形面+Z侧外热流变化Fig.12 Periodic variation of external heat flux of triangle+Zside after epoch
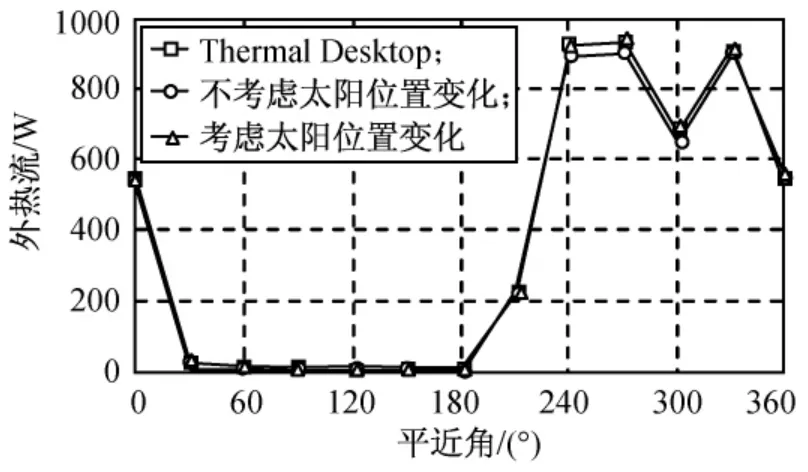
图13 圆环面-Z侧外热流变化Fig.13 Periodic variation of external heat flux of the ring-Zside after epoch
由图12、13可知:相对外热流角系数来说,用外热流辐射传递因子计算与Thermal Desktop软件更符合,相对偏差约1%。对三角形面+Z侧,直接投射的太阳辐射外热流为零,但会吸收部分圆环面-Z侧反射的太阳辐射外热流,在日照区,用角系数则无法考虑此影响,故与Thermal Desktop软件相比误差大于10%;对圆环面-Z侧,直接投射的地球红外辐射和反照辐射外热流为零,但会吸收三角形面+Z侧反射的地球红外辐射和反照辐射外热流,因其量级与太阳辐射外热流相比较小,在日照区影响不明显,但在地影区影响达20W,用角系数仍无法考虑此影响。
4 结论
本文对考虑轨道摄动的外热流计算进行了研究,重新定义了外热流角系数,采用辐射换热计算中的Gebhart方法,给出了外热流辐射传递因子概念,综合SGP4轨道模型,研究了考虑摄动与太阳矢量变化的外热流计算方法,并与Thermal Desktop软件结果进行对比。结果表明:(1)太阳位置变化及摄动影响可忽略时,本文算法计算结果与Thermal Desktop软件吻合良好,证明本文算法体系的正确性。(2)一般,航天器面元外热流存在相互遮挡与反射,用角系数计算外热流不能很好地反映真实状况,故须用辐射传递因子计算。(3)轨道摄动对外热流计算的影响随在轨运行时间而积累。运行时间较短时,不考虑摄动导致的误差较小,但随运行时间增加,摄动对外热流影响将逐步增大,不考虑摄动的计算结果将完全不能反映外热流真实变化状况。(4)与轨道摄动相比,太阳矢量变化对外热流的影响较缓慢,但随在轨运行时间增加其影响亦不可忽略,且具一定复杂性。根据入轨点轨道参数的不同,太阳矢量变化对外热变化趋势、外热流峰值及地影区位置均会产生影响。太阳辐射在外热流中所占份额极大,考虑太阳矢量变化的意义重要。(5)轨道摄动和太阳矢量变化均会对地影区位置产生严重影响。由于地影区只存在地球红外辐射外热流,进出地影区瞬间外热流会发生剧烈跳变。因此,为准确计算航天器所受外热流,须考虑摄动和太阳矢量变化的影响。综上,一般情况下决定航天器内部换热关系的导热热阻和红外辐射换热因子具定常性,航天器所受外热流是航天器瞬态温度场决定因素。准确计算外热流,可为热设计的有效性验证提供更可靠依据,本文方法有重要的工程应用意义。
[1]张 涛,孙 冰.计算近地轨道航天器空间外热流的RUD方法[J].宇航学报,2009,30(1):1-6.
[2]闵桂荣.卫星热控制技术[M].北京:中国宇航出版社,1991.
[3]赵立新.轨道空间外热流计算的一种新方法[J].光学精密工程,1995,3(6):80-85.
[4]安敏杰,程惠尔,李 鹏.空间对接机构太阳外热流的计算与分析[J].上海航天,2006,23(1):22-26.
[5]翁建华,潘增富,闵桂荣.空间任意形状凸面的轨道空间外热流计算方法[J].中国空间科学技术,1994,14(2):11-18.
[6]余其铮.辐射换热原理[M].哈尔滨:哈尔滨工业大学出版社,2000.
[7]HOOTS F R.A short efficient analytical satellite theory[R].AIAA,80-1659.
[8]VALLADO D A.Revisiting spacetrack report#3[R].AIAA,2006-6753.
[9]李万林.卫星空间外热流轨道参数ψ0,Ω0和ω0计算[J].中国空间科学技术,1993,(6):58-61.
[10]金学宽.近地航天器受照角系数的矢量计算法[J].宇航学报,1984,5(1):69-80.

