热声驱动的气-液双作用行波热声制冷机
张 爽 陈燕燕 罗二仓
(1中国科学院理化技术研究所低温工程学重点实验室 北京 100190)
(2中国科学院研究生院 北京 100049)
热声驱动的气-液双作用行波热声制冷机
张 爽1,2陈燕燕1罗二仓1
(1中国科学院理化技术研究所低温工程学重点实验室 北京 100190)
(2中国科学院研究生院 北京 100049)
提出了一种热声驱动的气-液双作用行波热声制冷机,对其性能进行了数值模拟分析。计算结果表明,在平均工作压力3.0 MPa,发动机定壁温加热温度440℃工况下,系统谐振频率为12.76 Hz,在-20℃制冷温度以及环境温度为27℃的情况下获得0.708 kW制冷量,整机的制冷系数(制冷量除以加热量)为0.512。在350℃、440℃以及550℃定壁温加热下,系统能够达到的最低制冷温度分别为-62.3℃、-68.3℃以及-70.8℃。系统整机相对卡诺效率在制冷温度变化范围内存在最大值。较低的发动机加热温度更有利于系统的热声转换,当发动机加热温度为350℃时,系统在-45℃制冷温度下达到25.30%最大相对卡诺效率。
热声驱动 双作用 行波热声制冷机 液体活塞
1 引言
蒸气压缩式制冷因其具有较高效率而在制冷及空调产业中广泛应用,然而其工质多为氯氟烃(CFC)和氢氯氟烃(HCFC),造成了臭氧层破坏、温室效应等诸多环境问题。随着人们对环境以及能源高效利用的逐渐重视,热声制冷机受到广泛关注。热声制冷机通过强声场条件下振荡气体与狭窄流道固体之间的热交换实现热量从低温向高温的输运,多采用氦气、氮气等惰性气体作为工质,对环境友好。热声制冷机可由电驱动,也可由热声驱动。热声驱动的热声制冷机可以实现完全无机械运动部件运行,具有可靠性高和使用寿命长的优点。在热声制冷机中,行波热声制冷机因其内在遵循斯特林循环而具有潜在高效率[1]。以上这些优点无疑使得热声驱动的行波热声制冷机具有很好的应用前景。
2006年,罗二仓等人采用高效聚能型行波热声发动机驱动行波热声制冷机,在发动机加热量为2.2 kW时获得最低制冷温度-64.4℃,在制冷温度为-22.1℃时获得了250 W的制冷量[2]。2011年,于波等人继续采用高效聚能型行波热声发动机驱动另一种结构的行波热声制冷机,在-20℃获得340 W制冷量,整机制冷系数(制冷量除以发动机加热量COP)达到0.16,在0℃获得469 W制冷量,整机制冷系数为0.216[3]。但是由于发动机和制冷机谐振管部分仍是以驻波声场为主,谐振管中贮存了一部分声功没有得到充分的回收利用,同时存在较大流动损失,限制了热声驱动行波热声制冷机的整机效率。
2012年,罗二仓、李东辉等人提出了一种气-液双作用行波热声发动机,这种发动机采用环路对称结构,并在U型谐振管中引入水作为液体活塞,声功在环路中得到充分地回收,使得发动机具有较高的效率[4]。在这一基础上,本文提出一种热声驱动的气-液双作用行波制冷机,采用数值模拟分析了制冷机的工作特性,并考察了发动机在不同加热温度下,制冷机制冷量以及整机相对卡诺效率随制冷温度的变化特性。
2 热声驱动的气-液双作用行波热声制冷机流程及结构参数
热声驱动的气-液双作用行波热声制冷机的结构如图1所示。为了使结构更加对称,在环路中串接入两个完全相同的发动机单元和两个完全相同的制冷机单元。发动机单元包括主水冷器、回热器、加热器、热缓冲管、次水冷器和U型谐振管,其结构尺寸参考文献 [4],为了查阅方便,表1给出了发动机单元的主要结构尺寸。制冷机单元包括主室温端换热器、回热器、冷头、热缓冲管、次室温端换热器以及U型谐振管,结构尺寸如表2所示。U型谐振管主要由连接管1、缓冲腔、U型管以及连接管2构成,由于发动机与制冷机的横截面积不同,连接管2包括一段等横截面积的弯管段和一段变横截面积的锥形管段。U型谐振管竖直放置,在U型管中充入水作为液体活塞,其他热声核心部件呈水平放置,充入氦气作为气体工质。在缓冲腔中,采用弹性膜将气液分开。
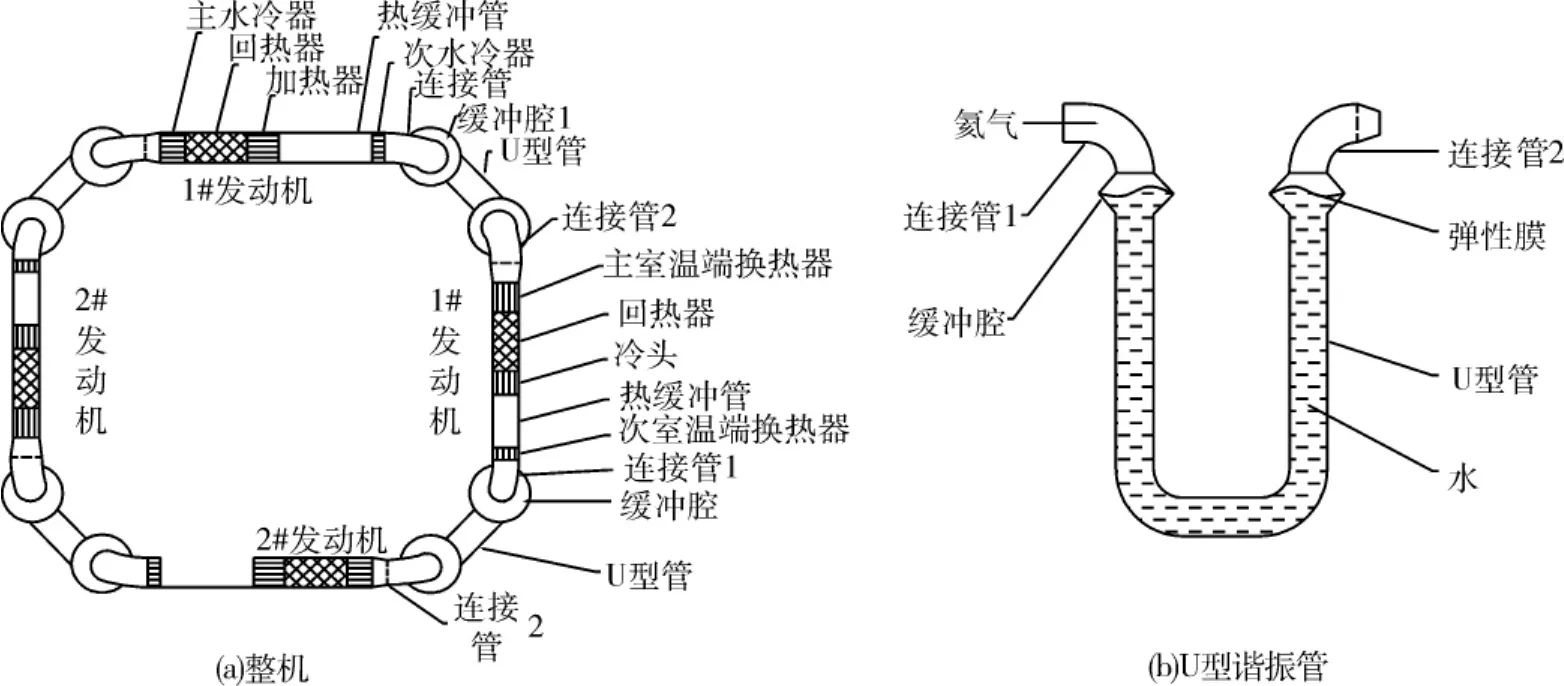
图1 热声驱动气-液双作用行波热声制冷机结构示意图Fig.1 Schematic of a thermoacoustically-driven double-acting traveling wave thermoacoustic refrigerator with liquid piston

表1 热声发动机单元主要结构参数Table 1 Dimensions of thermoacoustic heat engine unit

表2 热声制冷机单元主要结构参数Table 2 Dimensions of thermoacoustic regenerator unit
与文献[2-3]中的热声驱动行波热声制冷机相比,该制冷机在U型谐振管中充入水作为液体活塞,利用液体惯性,能够有效地降低谐振管的尺寸,使得系统结构更加紧凑,同时有利于降低系统的谐振频率;环形结构解决了声功回收的问题,发动机产生的声功,除了自身消耗的小部分外,绝大部分声功均进入到制冷机中,驱动制冷机工作,声功得到了有效利用,使得该热声驱动热声制冷机具有较高的效率;此外,对称结构也有利于发动机与制冷机相互之间的匹配。
3 热声驱动的气-液双作用行波热声制冷机性能分析
3.1 计算模型
根据经典热声学理论,本文对热声驱动的气-液双作用行波热声制冷机进行了数值模拟,模拟中采用了DeltaEC6.2软件[5]。对于气体工质,其控制方程如下[6]:
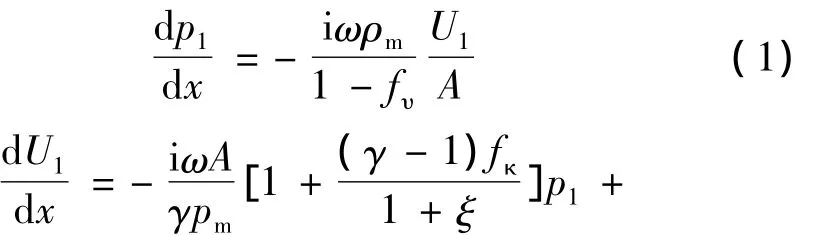
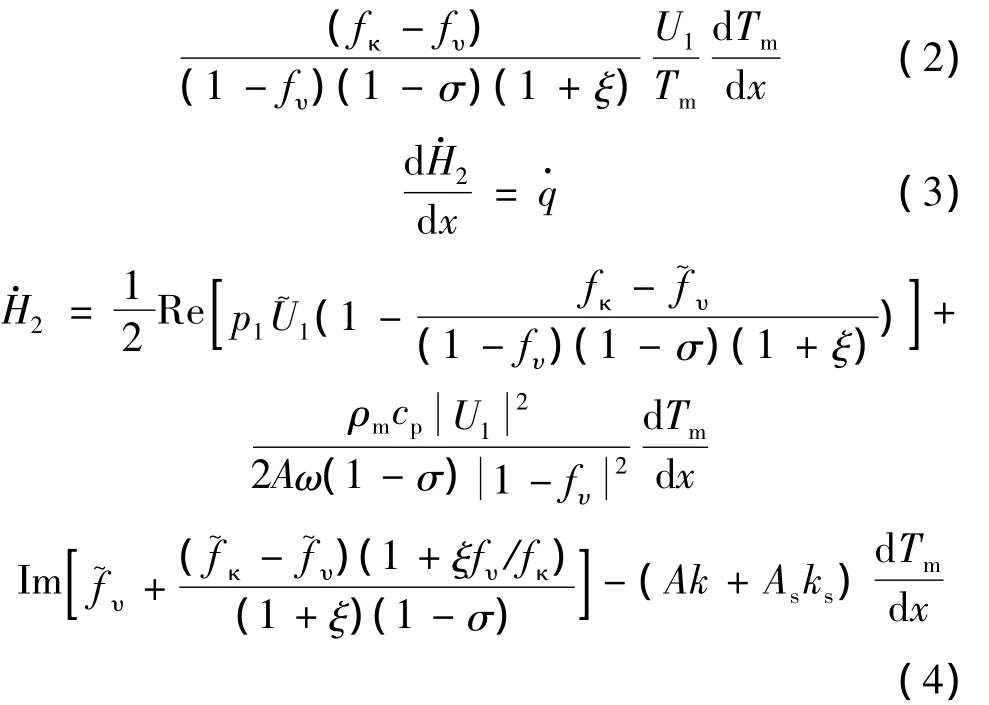
其中:p1和U1是一阶压力波动幅值和体积流率,i是虚数符号,ω是角频率,A为流道截面积,ρm,Pm,Tm分别表示气体的平均密度、压力和温度,γ,cp,k,σ为气体的比热比、比定压热容、热导率和普朗特数,复变量fυ和fκ与流道的几何参数和工质的物性参数有关,As和ks表示流道固体的截面积和热导率,ξ是壁面热物性参数的修正系数,Re和Im分别表示取实部和虚部,~表示取复数的共轭,||为复数的幅值,H·2为总功,q·为单位长度的加热量。
对于U型谐振管中的液柱,将其视为不可压缩流体,采用DeltaEC6.2软件中的IESPEAKER模块进行模拟,其控制方程为[5]:
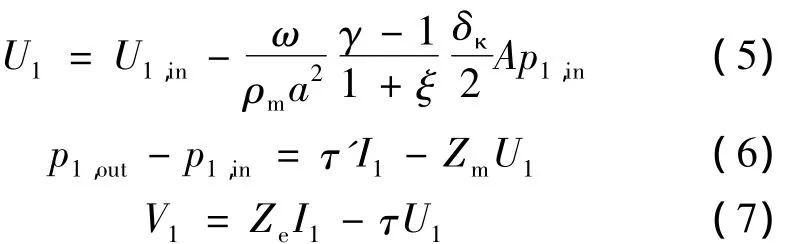
其中:U1,in为IESPEAKER入口体积流率,a为声速,δκ为热穿透深度,p1,out,p1,in分别为 IESPEAKER出口、入口处压力波动幅值,τ=-τ’为声电常数,模拟U型谐振管内液柱时为0,Zm为机械阻抗,Ze为电阻抗,模拟U型谐振管内液柱时取为0,V1、I1分别为IESPEAKER输入电压、电流,在模拟液柱时取为0。
由于系统是对称结构,在模拟中只对1#发动机主水冷器入口至1#制冷机连接管2出口这一区间进行了计算分析。在整个环路中,体积流率与压力波动的相位分别变化了360°,因此,1#制冷机连接管2出口处的体积流率与压力波动幅值,同1#发动机主水冷器入口处相比,相位分别变化了180°。计算中平均工作压力为3.0 MPa,发动机采用定壁温加热,主水冷器、次水冷器、主室温端换热器以及次室温端换热器均固定壁温为27℃。
3.2 热声驱动的气-液双作用行波热声制冷机性能分析
本节主要针对固定工况下(平均工作压力3.0 MPa,发动机定壁温加热温度440℃,制冷温度-20℃)热声驱动的气-液双作用行波热声制冷机性能参数沿程分布进行了分析,如图2-图6所示。由于模拟中采用IESPEAKER模块模拟水柱,没有体现出水柱的长度,因此在图2-图6中液柱的位置处出现某些性能参数的突变。(位置说明:发动机0—1.03 m,其中主水冷器0—0.04 m、回热器0.04 m—0.14 m、加热器0.14 m—0.19 m、热缓冲管0.19 m—0.34 m、次水冷器0.34 m—0.36 m、U型谐振管0.36 m—1.03 m;制冷机1.03 m—1.656 m,其中主室温端换热器1.03 m—1.074 m、回热器1.074 m—1.111 m、冷头1.111 m—1.161 m、热缓冲管1.161 m—1.311 m、次室温端换热器1.311 m—1.326 m、U型谐振管1.326 m—1.656 m)
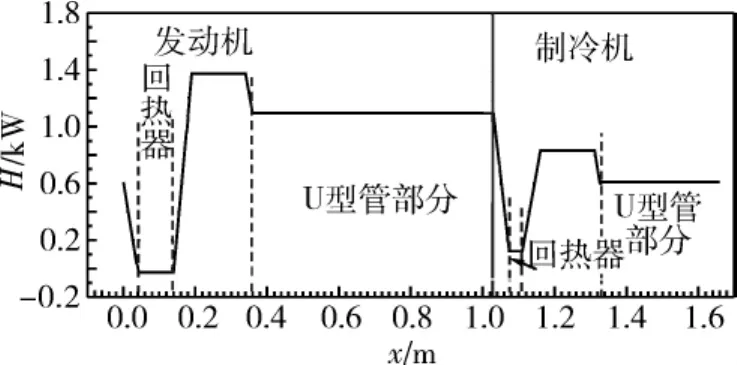
图2 总能流沿程分布Fig.2 Distribution of total energy
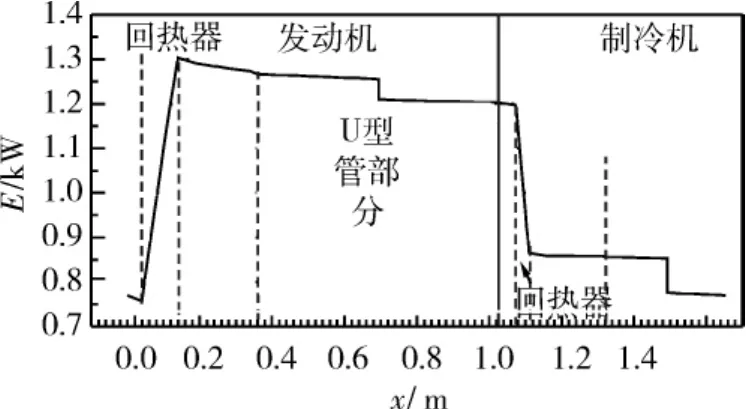
图3 声功沿程分布Fig.3 Distribution of acoustic power
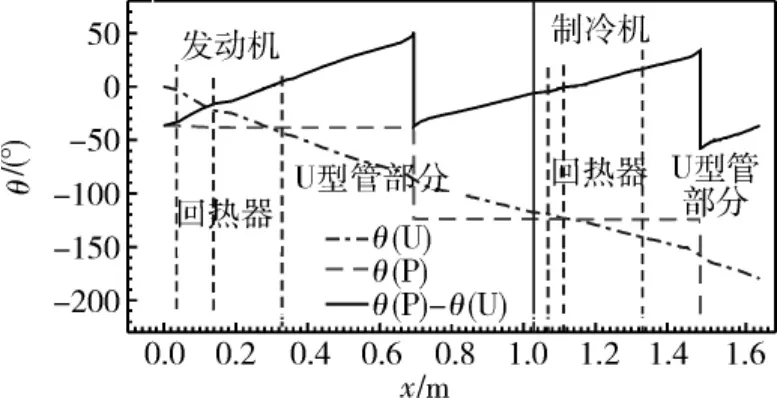
图4 相位沿程分布Fig.4 Distribution of phase angle
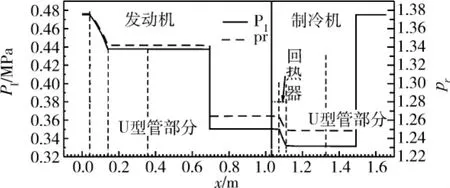
图5 压力波动幅值与压比沿程分布Fig.5 Distributions of pressure amplitude and pressure ratio
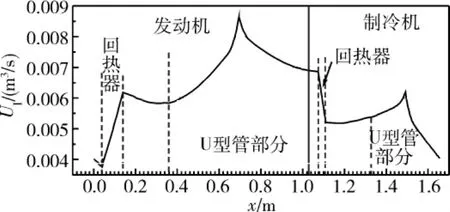
图6 体积流率沿程分布Fig.6 Distribution of volume flow rate
根据数值模拟结果,装置在工作时,系统谐振频率为12.76 Hz,发动机加热器加热热量为1.38 kW(定壁温加热,加热温度为440℃),制冷机制冷量0.708 kW(制冷温度为-20℃),如图2所示,H为总能流。
图3给出了声功流E沿装置长度x的沿程分布。从图中可知,0.757 kW的声功进入回热器室温端,在回热器中得到放大,回热器中产生净声功率0.546 kW。在热缓冲管、次水冷器、U型谐振管以及主水冷器中,均有声功的小幅损耗,共为0.113 kW(占回热器产生净声功率的20.6%),因此,在440℃定壁温加热下,发动机加热量为1.38 kW,产生净声功率0.433 kW,发动机第一热效率为31.37%。由此可知,发动机中回热器产生的净声功率,有79.4%用以驱动制冷机,声功得到了较充分的利用。在制冷机中,共消耗声功率0.433 kW,其中回热器消耗声功率0.332 kW,制冷温度为-20℃时制冷量为0.708 kW,制冷机COP达到1.64。故该热声驱动的气-液双作用行波热声制冷机的整机制冷系数为0.513。
对于热声热机来说,压力波动与体积流率之间的相位差决定着热声转换效率。体积流率可以表示为与压力波动同相的行波分量和与压力波动相位相差π/2的驻波分量之和,行波分量能更有效地产生声功[7]。因此,声场中的行波分量越大,越有利于热声之间的转换。图4给出了压力波动幅值P1与体积流率U1的相位θ之间的关系。从图中可知,压力波动与体积流率的相位在制冷机回热器中基本达到同相,因此可以认为,制冷机部分的结构比较理想;在发动机回热器中,压力波动与体积流率相位略偏离同相,但声场中的行波分量仍较大;总的来说,在给定的运行工况下,发动机与制冷机的结构均较为理想,但是仍有继续优化的空间。
图5-图6分别给出了压力波动幅值P1与体积流率U1的沿程分布。结合图4可知,在发动机和制冷机的回热器中,由于阻力的作用导致压力波动幅值线性下降,同时,由于液柱较大的惯性作用,压力波动的相位与幅值均会发生较大的变化。而U型谐振管中的液柱对体积流率的幅值与相位均无明显影响,体积流率在回热器中的也呈线性变化,且体积流率增大的方向与温度增加的方向相同。
3.3 制冷温度与制冷量
本节主要讨论发动机在不同加热温度下,制冷机制冷量以及整机相对卡诺效率随制冷温度的变化。
图7给出了在发动机不同加热温度下,制冷机制冷量随制冷温度的变化关系。从图中可知,制冷量随制冷温度近似呈线性变化。总体上,发动机的加热温度越高,制冷机能够获得的制冷量就越大,并且能够达到更低的制冷温度。在350℃、440℃以及550℃定壁温加热下,系统能够达到的最低制冷温度分别为-62.31℃、-68.34℃以及-70.84℃。在-20℃制冷温度下,350℃、440℃以及550℃定壁温加热所能获得的制冷量分别为434.46 W、707.92 W以及924.87 W。
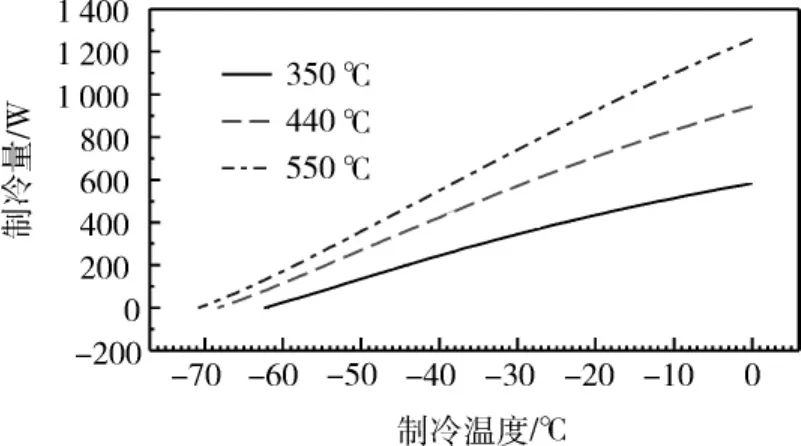
图7 制冷量随制冷温度变化关系Fig.7 Cooling power vs.cold-end temperature
对于制冷机的性能考察,除了制冷量,效率也是一个重要的指标。由于本节考察不同加热温度和不同制冷温度对效率的影响,为了更有比较性,系统的效率采用整机相对卡诺效率。对于热驱动的制冷机,其整机卡诺效率相当于工作在高温热源TH和室温T0之间的发动机卡诺效率与工作在室温T0与制冷温度TC之间的制冷机卡诺效率的乘积[8]。在本节中,发动机加热温度,即高温热源TH,分别为350℃、440℃以及550℃;室温T0为27℃;制冷温度TC由0℃变化至最低制冷温度。则整机的相对卡诺效率ζc可表示为:
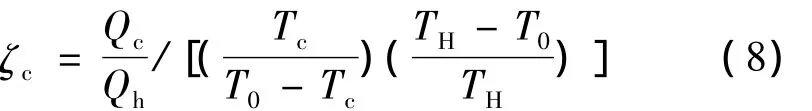
图8给出了发动机不同加热温度下,整机的相对卡诺效率随制冷温度的变化关系。总体上,当制冷温度降低时,系统的相对卡诺效率缓慢上升,达到最大值后急剧下降。发动机加热温度为550℃、440℃时,系统相对卡诺效率均在-47℃制冷温度下达到最大值,分别为16.51%、21.26%;发动机加热温度为350℃时,系统相对卡诺效率在-45℃制冷温度下达到25.30%最大相对卡诺效率。因此,当发动机加热温度较低时,系统能够获得的整机相对卡诺效率越高,系统的热声转换性能更为理想。可以认为,现有的系统结构更适用于较低加热温度下工作,这也有利于系统利用废热或太阳能驱动。
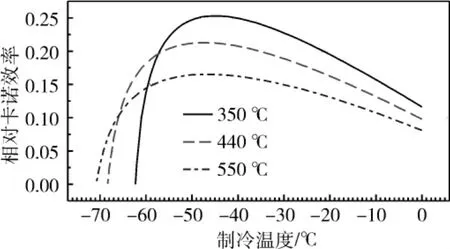
图8 相对卡诺效率随制冷温度变化关系Fig.8 Relative Carnot efficiency vs.cold-end temperature
4 结论
提出了一种热声驱动的气-液双作用行波热声制冷机,并对其性能进行了分析,该制冷机能够有效回收声功,具有较为理想的整机效率:
(1)计算结果表明,在平均工作压力3.0 MPa,发动机定壁温加热温度440℃工况下,系统谐振频率为12.76 Hz,在-20℃制冷温度下获得了0.708 kW制冷量,整机效率(制冷量除以加热量)为0.513。压力波动与体积流率的相位沿程分布较为理想。
(2)讨论了发动机不同加热温度下,制冷机制冷量以及整机相对卡诺效率随制冷温度的变化。在350℃、440℃以及550℃定壁温加热下,系统能够达到的最低制冷温度分别为-62.31℃、-68.34℃以及-70.84℃。系统整机相对卡诺效率在制冷温度变化范围内存在最大值。发动机加热温度为550℃、440℃时,系统相对卡诺效率均在-47℃制冷温度下达到最大值,分别为16.51%、21.26%;发动机加热温度为350℃时,系统相对卡诺效率在-45℃制冷温度下达到25.30%最大相对卡诺效率。
(3)系统还存在优化的空间。此外,对该制冷机的实验研究为下一步工作的重点。
1 Ceperley P.Gain and efficiency of a short traveling wave heat engine[J].J.Acoust.Soc.Am.,1985,77(3):1239-1244.
2 Luo E C,Hong L.Thermoacoustically driven refrigerator with double thermoacoustic-Stirling cycles[J].Appl.Phys.Lett.,2006,88(7):074102.
3 Yu B,Luo E C,Li S F,et al.Experimental study of a thermoacoustically-driven traveling wave thermoacoustic refrigerator[J].Cryogenics,2011,51:49-54.
4 Li D H,Zhang L M,Wu Z H,et al.Numerical simulation and experimental investigation of a gas-liquid,double-acting traveling-wave thermoacoustic heat engine[C].International Conference on Applied Energy ICAE 2012,Suzhou:2012.
5 Ward B,Clark J,Swift G.Design environment for low-amplitude thermoacoustic energy conversion,DELTAEC Version6.2 Users Guide,2008.
6 Swift G W.Thermoacoustics:a unifying perspective for some engines and refrigerators[M].New York:AIP Press,2002.
7 Yazaki T,Iwata A,Maekawa T,et al.Traveling wave themoacoustic engine in a loop tube[J].Phys.Rev.Lett.,1998,81(15):3128-3131.
8 陈光明,陈国邦.制冷与低温原理[M].北京:机械工业出版社,2009.
A thermoacoustically-driven double-acting traveling wave thermoacoustic refrigerator with liquid piston
Zhang Shuang1,2Chen Yanyan1Luo Ercang1
(1Key Laboratory of Cryogenics,Technical Institute of Physics and Chemistry,Chinese Academy of Sciences,Beijing 100190,China)
(2Graduate University of Chinese Academy of Sciences,Beijing 100049,China)
A thermoacoustically-driven double-acting traveling wave thermoacoustic refrigerator with liquid piston was proposed and analyzed.At the operating point with 3.0 MPa mean working pressure and 440℃ heating temperature,the resonant frequency was 12.76 Hz and the refrigerator provide 0.708 kW cooling power at-20℃cooling temperature and 27℃surrounding temperature.The COP of whole system was 0.512.Under different heating temperature with 350℃,440℃ and 550℃,the system could provide the lowest cooling temperatures of-62.3℃,-68.3℃ and-70.8℃.There was a maximum value of relative Carnot efficiency when the cooling temperature changed.Lower heating temperature was more suitable to this system.The highest relative Carnot efficiency of 25.30%at-47℃was achieved when the heating temperature was 350℃.
thermoacoustically-driven;double-acting;thermoacoustic refrigerator;liquid piston
TB651
A
1000-6516(2012)06-0005-05
2012-09-19;
2012-12-05
国家自然科学基金重大项目(No.50890181)、国家科技部973项目(No.2010CB227303)支持。
张 爽,女,23岁,硕士研究生。

