温度计的热响应时间对动态测温的影响

董 斌 周 刚 刘立强 熊联友 张 祥 张 亮

(1中国科学院理化技术研究所低温工程学重点实验室 北京 100190)

(2中国科学院研究生院 北京 100190)

温度计的热响应时间对动态测温的影响

董 斌1，2周 刚1刘立强1熊联友1张 祥1，2张 亮1

(1中国科学院理化技术研究所低温工程学重点实验室 北京 100190)

(2中国科学院研究生院 北京 100190)

基于导热模型分析了真空环境下使用陶瓷封装的铑铁温度计测量固体表面或内部温度的热响应时间，并进一步分析了在动态测温中，温度计的热响应时间对测量的影响。分析计算结果及实验表明，在动态测温中，热响应时间会使温度计测得的温度波动幅值小于被测温度，并且热响应时间越大，测得的温度波动幅值越小。

铑铁温度计 热响应时间 动态测温

1 引言

Gifford-McMahon(G-M)制冷机广泛应用于低温恒温器中，但是其冷头的温度波动较大，在4.2 K时波动幅值约有300 mK［1］。样品架处的温度会受此温度波动的影响，为了准确的测量样品架处的温度，需要分析温度计的热响应时间对测量的影响。

在低温下，铑铁温度计是常用的一种宽温区温度传感器。常见的铑铁温度计的封装形式与工业铂电阻温度计类似，内部是直径为0.05 mm的铑铁合金丝缠绕在骨架上，外部为陶瓷套管，中间填有增强导热的填料［2-3］。这种封装结构的温度计尺寸较大，热响应时间也比较大。在动态测温中，热响应时间对测量的影响一方面表现为，温度计需要一定的时间才能与被测温度达到平衡;另一方面表现为，若被测温度是周期性波动的，那么所测得的结果中，温度的波动幅值会小于被测物体的温度波动幅值。本文对导热模型下的温度计热响应时间做了理论分析，通过数值计算获得了热响应时间对周期性波动的温度的测量影响，并用实验验证了这一分析计算结果。

2 理论模型

温度计的时间常数通常定义为，温度计自身温度和被测物体温度之间的过余温度达到初始过余温度的 36.8%时［4］，所经过的时间，即:

式中:θ为温度计的过余温度，T为温度计的温度，T0为温度计的初始温度，T∞为被测物体的温度，τ为时间常数，t为时间。实验中使用了LakeShore的温度计，根据其产品说明，温度计的热响应时间定义为一倍的时间常数(Temperature Measurement and Control Catalog，LakeShore)。

对于在低温恒温器内测量样品架温度的情况，低温恒温器内的真空度约为1×10-5Pa，并且铑铁温度计是安装在一个小孔内的，残余气体的导热和热辐射对温度计的影响均可以忽略不计，因此温度计的传热可以简化为2维轴对称的导热模型，如图1所示。

图1 温度计的2维轴对称导热模型Fig.1 Two dimensional axisymmetric heat conduction model of thermometer

图1中，a为温度计内铑铁合金丝的半径，b为温度计的半径，长度为h。假设温度计的初始温度为T0，在t＞0时刻，温度计外表面处的温度为T1。铑铁丝在低温下的导热系数大于陶瓷，并且体积很小，在理论分析中暂不考虑温度计的自热效应，这样简化后，温度计的内壁a处的边界条件可视为绝热边界，并且a处的温度即为温度计的测量温度。这一传热问题可以表示为［5］:

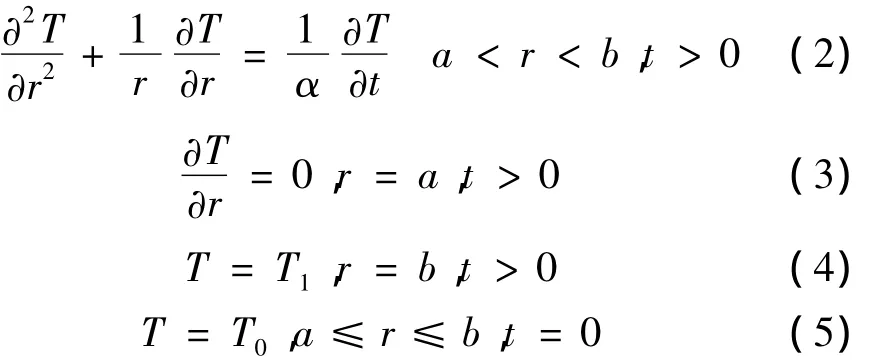
上述各式中:α为温度计外壳材料的热扩散系数，α =k/ρc，k为导热系数，ρ为密度，c为比热容。引入过余温度θ，对上式求解可得:

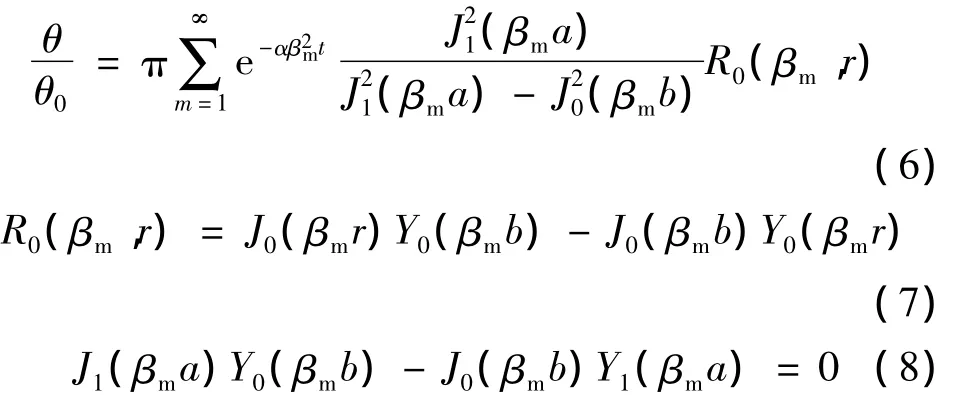
式中:J和Y分别为第一类和第二类贝塞尔函数，βm是方程(8)的正根。把 r=a和 θ/θ0=36.8%以及陶瓷封装材料的热扩散系数α代入上式，即可采用数值解法求得温度计的热响应时间t。但在低温下，材料的热扩散系数并不容易获得，因此通常是通过实验的方法来获得温度计在不同温度下的热响应时间。

当被测物体的温度是周期性波动时，即r=b处的边界条件为T=f(t)，假设该温度为一正弦波，即:

f(t)=Tm+Tfsin(ωt+ φ) (9)

式中:Tm为温度波动的平均值，Tf为波动幅值，ω/2π为频率，t为时间，φ为相位。导热微分方程(2)的解可表示为:

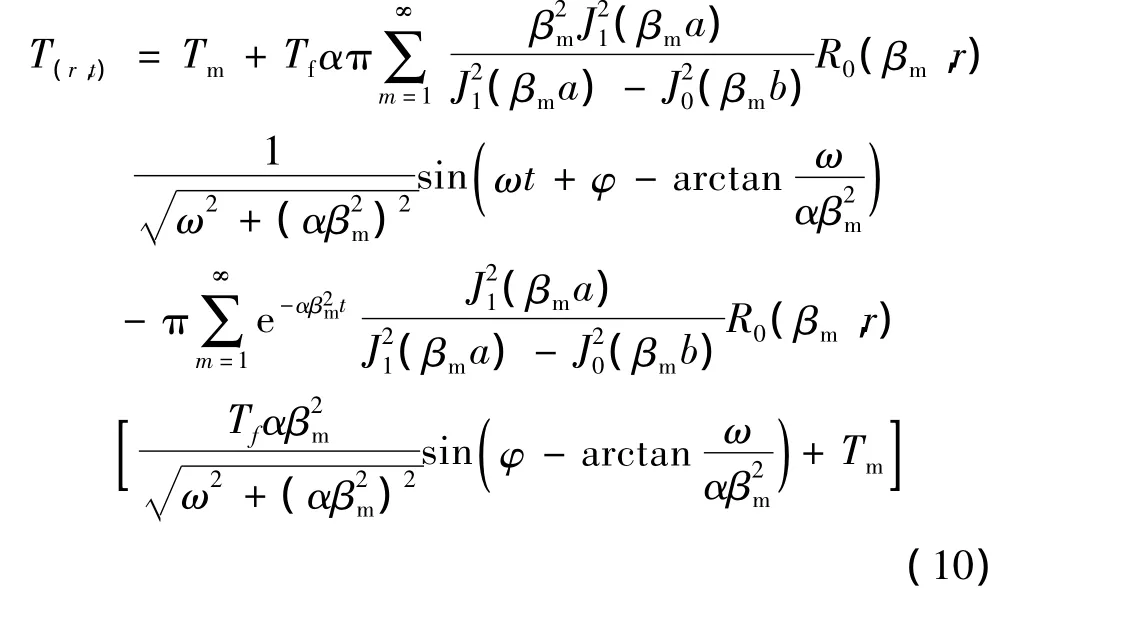
从式(10)中可以看出，第一项为稳态项，表明温度稳定后的平均值与被测物体一致;第二项为随时间变化的温度，表明稳定后的温度与被测物体是以相同的频率随时间变化，但是幅值和相位均不同;第三项随时间增加而衰减，当t→∞时，第三项逐渐趋于零。

G-M制冷机的二级冷头在4.2 K时的温度波动幅值大于300 mK，波动频率约为1 Hz，假设其温度波动曲线为:

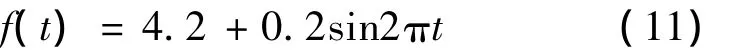
假设温度计的热响应时间分别为0.8 s和1.2 s，初始温度也为4.2 K，可得T(a，t)在5 s内的计算结果，如图2所示。图2中，Tb为温度计的边界b处的温度，Ta1和Ta2分别是热响应时间为0.8 s和1.2 s时，温度计边界a处的温度。从图中可以看出，经过1 s后，温度计的温度就进入了稳定状态。在热平衡后，热响应时间为0.8 s和1.2 s时，温度计测得的温度波动幅值分别为230 mK和190 mK，为被测温度波动幅值的57.5%和42.3%。这表明，温度计的热响应时间会使温度计在动态测温过程中，测得的温度波动幅值小于被测物体的温度波动幅值，并且热响应时间越大，测得的幅值越小。

图2 温度计内外表面温度-时间曲线Ta1:热响应时间0.8 s;Ta2:热响应时间1.2 sFig.2 Temperature-time curves of inner and outer surface of thermometer

3 动态测温实验

实验在一个使用G-M制冷机冷却的低温恒温器中进行。制冷机冷却的低温恒温器具有简单的结构，其主要结构有G-M制冷机、低温恒温器筒体、辐射屏、样品架以及一些附件(真空抽嘴、引线接头等)组成，低温恒温器的结构简图如图3所示。样品架直接与制冷机的二级冷头相连接，样品架靠近冷头的一端，缠绕有康铜加热丝，用于调节样品架的温度。样品架的另外一端安装有标定过的铑铁温度计和Cernox温度计。铑铁温度计安装在小孔内，孔内填充有阿皮松脂 N脂(Apiezon N Grease)，以增强导热。Cernox温度计是贴片式封装，使用清漆粘在样品架的表面，外面包扎多层绝热材料来减弱热辐射对温度计的影响。加热器引线和温度计测量引线分别在制冷机的一级冷头和二级冷头上缠绕制作热沉，以减小引线漏热对测量的影响。Cernox温度计的测量信号同时作为控温仪的反馈信号，用于控制样品架的温度。分别设定样品架的温度为4.2 K和20 K，待样品架的温度稳定后，记录两支温度计的测量数据。

图3 制冷机冷却的低温恒温器Fig.3 Cryostat equipped with cryocooler

4 理论与实验结果比较

在4.2K温度下，铑铁温度计和Cernox温度计的热响应时间分别为0.8s和15ms(Temperature Measurement and Control Catalog，LakeShore)。由于 Cernox温度计的热响应时间非常小，它测量的温度结果也非常接近真实值，因此使用Cernox温度计的测量结果作为基准，铑铁的测量结果与其进行对比。图4和图5分别是样品架的温度控制在4.2 K和20 K附近时，温度稳定后两支温度计的测量结果。

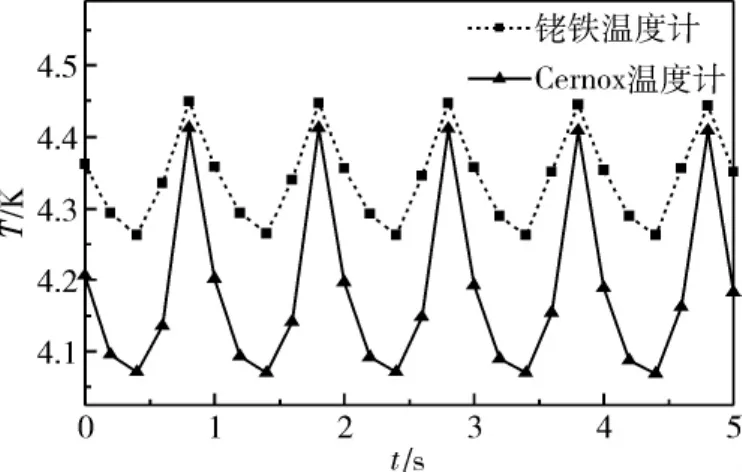
图4 样品架温度为4.2 K时两支温度计的测量结果Fig.4 Measurement result of two thermometerswhen sample holder at 4.2 K

图5 样品架温度为20 K时两支温度计的测量结果Fig.5 Measurement result of two thermometers when sample holder at 20 K

从图4中可以看出，Cernox温度计测量的温度约为4.06—4.41 K，波动的峰峰值约为350 mK，铑铁温度计的测量结果为4.26—4.46 K，波动的峰峰值为200 mK。铑铁温度计测得的温度波动峰峰值与Cernox测得的峰峰值比值为57.1%，与理论计算结果相符，误差主要来自于铑铁温度计的安装方式引起的接触热阻，以及使用Cernox温度计的测量结果代替真实的样品架处温度波动。图4中还可以看出，铑铁温度计的测量结果平均值高于Cernox的测量结果，这主要是由于铑铁温度计的标定不确定度为0.1 K，而Cernox温度计在4.2 K下的测量不确定度为8.4 mK。

图5中，铑铁温度计和Cernox温度计的测量结果中，温度波动的峰峰值分别为160 mK和470 mK，比值为34%。这是因为随着温度的升高，陶瓷材料的导热系数和比热容均增大，但是比热容增加的更快，因而导致20 K下的热扩散系数小于4.2 K下的，表明铑铁温度计在20 K时的热响应时间变长了。与图2中的数值模拟结果相比，可知此时铑铁温度计的热响应时间已经大于1 s。图5中，铑铁温度计测得的温度平均值小于Cernox温度计的测量结果，这也是由于两支温度计的标定精度不同而导致的。

5 结论

在使用温度计测量真空环境下的固体表面或内部温度时，温度计的热响应时间主要与其封装材料的热物性参数和封装尺寸有关。在动态测温中，热响应时间会使温度计的测量结果中温度波动幅值小于被测物体的实际温度波动幅值，并且热响应时间越大，测得的幅值越小。对导热模型下的温度计热响应时间进行了理论分析和数值计算模拟，并通过实验验证了这一结果。

1 Nakamura Daiki，Hasegawa Yasuhiro，Murata Masayuki，et al.Reduction of temperature fluctuation within low temperature region using a cryocooler［J］.Review of Scientific Instruments，2011，82(4):044903.

2 阎守胜，陆果编著.低温物理实验的原理与方法［M］.北京:科学出版社，1985.

3 毛玉柱，姚全发.RF27型陶瓷铑铁电阻温度计的稳定性［J］.自动化仪表，1994，15(5):12-14.

4 杨世铭，陶文铨.传热学［M］.北京:高等教育出版社，1998.

5 Ozisik M N著，余昌铭主译.热传导［M］.北京:高等教育出版社，1983.

Effect of thermal response time for thermometer on dynamic temperature measurement

Dong Bin1，2Zhou Gang1Liu Liqiang1Xiong Lianyou1Zhang Xiang1，2Zhang Liang1
(1Key Laboratory of Cryogenics，Technical Institute of Physics and Chemistry，Chinese Academy of Sciences，Beijing 100190，China)(2Graduate University of Chinese Academy of Sciences，Beijing 100190，China)

Thermal response time of ceramic packaging rhodium-iron thermometer was analyzed when used to measure the surface or inner temperature of solids in vacuum based heat conduction model.The influence of thermal response time on dynamic temperature measurement was analyzed too.The numerical simulation and experiment results show that the thermal response time causes a little amplitude of temperature oscillation in dynamic temperature measurement.Furthermore the larger thermal response time it is，the smaller amplitude becomes in measurement results.

rhodium-iron thermometer;thermal response time;dynamic temperature measurement

TB663

A

1000-6516(2012)06-0033-04

2012-11-07;

2012-12-03

中国科学院知识创新工程重要方向项目资助(YYYJ-1124)。

董 斌，男，27岁，博士研究生。