考虑剪切变形的圆弧深拱参数共振稳定性分析

赵洪金，刘 超，2，董宁娟，吴敏哲

(1.西安建筑科技大学 土木工程学院，西安 710055;2.西安建筑科技大学 理学院，西安 710055;3.中国飞机强度研究所，西安 710065)

圆拱是一种被广泛应用于土木工程实际中的建筑结构.在外部压力作用下，圆拱的受力分析和稳定计算是工程设计所关心的主要问题，现有文献多针对浅拱动力稳定性分析［1－5]。这些研究成果代表了拱结构动力稳定问题的研究现状，但是这些研究工作都没有考虑剪切变形的影响。目前高速公路中的小跨径拱桥有相当一部分是大曲率深拱桥。当拱的圆心角较小、弧长较短时，截面尺寸相对于跨径来说较大，剪切变形［6]的影响不能忽略，此时是深拱［7]问题。

在土木、机械等实际工程中两端铰支边界条件是很少采用的，采用较多的固支边界条件。但是铰支边界条件的研究可以为固支边界的研究提供理论上的借鉴。本文根据能量法，建立以位移为基本未知量的圆拱总势能，从Hamilton原理出发，建立了考虑剪切变形的圆弧深拱的动力稳定微分方程，利用Galerkin方法将其转化为二阶常微分Mathieu型参数振动方程，求得周期解所包围的动力不稳定区域。探讨了圆弧深拱发生参数振动的动力稳定性问题，分析了剪切变形、圆弧半径、圆心角等参数对圆弧深拱动力稳定性的影响，为结构工程动力分析与设计提供参考依据。

1 圆弧深拱微分方程

如图1所示，深拱截面形心沿切向方向的位移为u、沿径向方向的位移为v、横截面绕轴的转角为ψ。

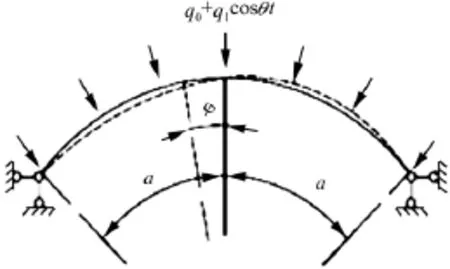
图1 两铰圆弧深拱反对称失稳Fig.1 Asymmetrical buckling of hinged circular deep arch

拱轴的轴向应变ε由两部分组成:由于截面形心位移u引起的轴向应变为由于径向位移v引起的应变为则:

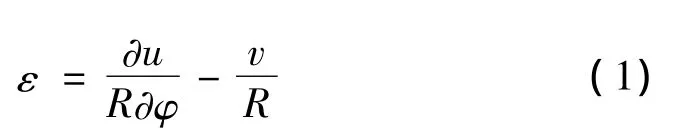
假设拱轴不可压缩，即ε=0，得到:

因截面转角ψ引起的曲率增量为:

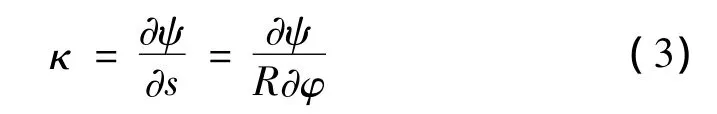
截面剪应变为:

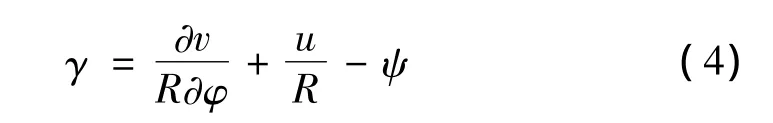
因此圆弧深拱应变能为:

外力势能为:

系统的动能为:

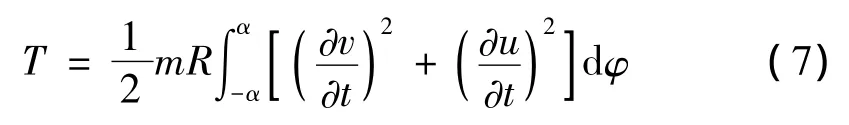
根据Hamilton原理，有:

分别对u，ν，ψ进行变分，得到径向周期荷载作用下圆弧深拱的动力稳定微分方程:

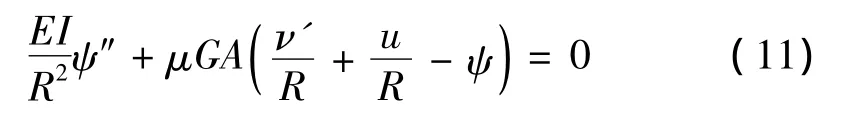
式中:m为单位长度拱的质量;E为拱的弹性模量;G为拱的剪切模量;A为截面面积;I为截面惯性矩;μ为截面的剪切变形系数。

考虑两铰圆弧拱在径向均布荷载作用下的弹性失稳为反对称失稳［8]，位移取如下级数形式:

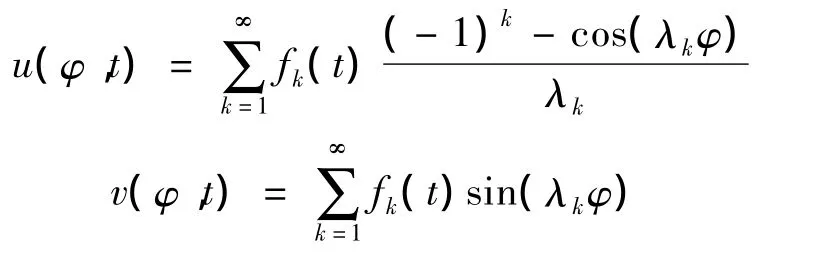
其中λk=/α，α为拱的圆心角，满足拱的边界条件，消去变量ψ方程转化为:

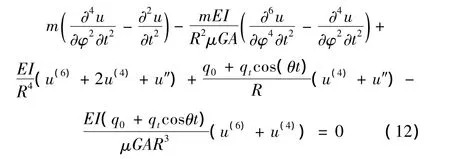
根据正交性条件［1]:

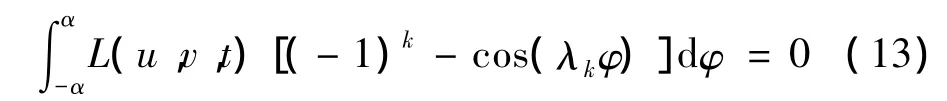
将式(13)代入式(12)后，利用Galerkin方法进行离散，可得到以下常微分方程

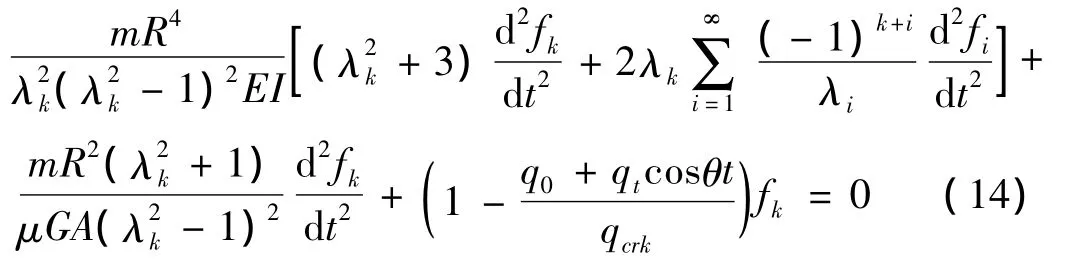
式中qcrk表示第k个临界荷载值:

考虑一阶弹性失稳为反对称失稳，临界系数λ1=π/α，对应的一阶临界荷载为:

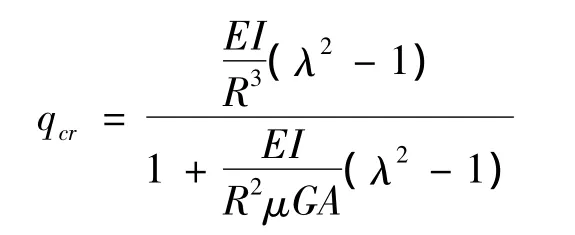
结果与文献［7] 计算的相同。将式(14)写成矩阵形式:

为了确定由周期解所包围的不稳定区域，设式(15)有周期4π/θ的周期解为:

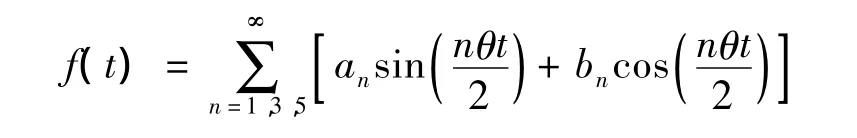
代入式(15)整理合并同类项，根据周期解存在的条件得到临界频率方程为:

式中:

在求主动力不稳定区域时，可取方程式(17)第一阶主子式:

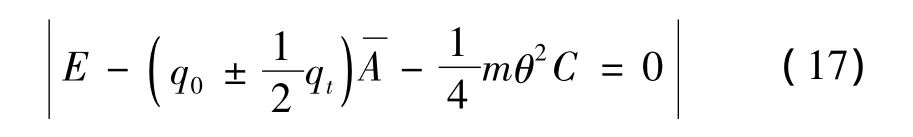
第一近似得到临界频率公式为:

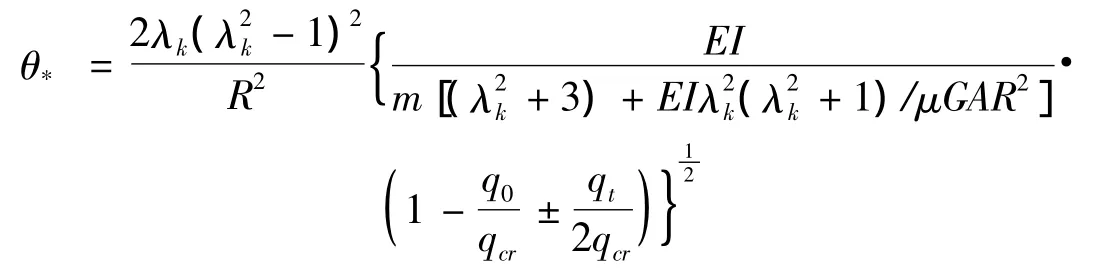
由此即可确定出位于θ=2Ω附近的动力不稳定区域，便有足够的精确度。

对于周期2π/θ的周期解为:

偶数决定的动力不稳定区域，也可得到相似的方程，求解过程从略。

3 算例分析

模型拱参数:两铰圆弧拱，横截面为矩形截面，结构尺寸b×h=1 m×1 m，面积A=1 m2，材料的弹性模量 E=2.1 ×105MPa、剪切模量 G=8.4 ×104MPa，截面的剪切修正系数 μ =5/6［12]，截面面积二阶矩I=bh3/12=1/12 m4。

图2 两铰圆弧模型深拱Fig.2 Hinged circular model deep arch

由图3可知，当圆心角为固定值时，随着圆弧深拱半径增加，结构发生参数共振时的频率降低，动力不稳定区域迅速扩大，说明半径越大，发生参数共振的可能性也越大，因此圆弧半径是决定拱结构动力不稳定区域的重要因素。

由图4可知，当半径一定时，随着圆心角的增加，相应的结构发生参数共振时的频率也降低，动力不稳定区域扩大，说明圆心角越大，发生参数共振的可能性也越大，可见圆心角也是决定拱结构动力不稳定区域的重要因素。但对动力不稳定区域的影响相比半径要小一些。

由图5和图6可知，圆弧拱发生参数共振时，考虑剪切变形的动力不稳定区域要小于不考虑剪切变形时的动力不稳定区域。

在矢跨比较小时，剪切变形对深拱的临界荷载值以及结构发生参数共振时的频率影响较大，因此对动力不稳定区域的影响比较明显，但随着失跨比增加，对动力不稳定区域的影响逐渐减小。

图3 半径对圆弧深拱动力不稳定区域的影响Fig.3 Effect of radius on principal regions of dynamic instability for circular deep arch

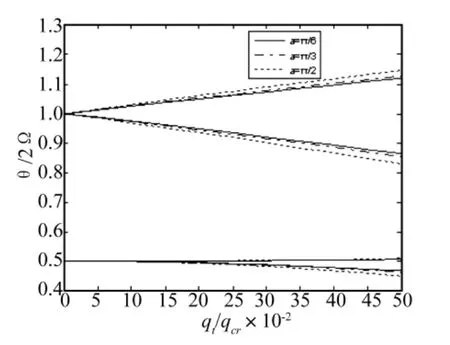
图4 圆心角对圆弧深拱动力不稳定区域的影响Fig.4 Effect of central angle on principal regions of dynamic instability for circular deep arch

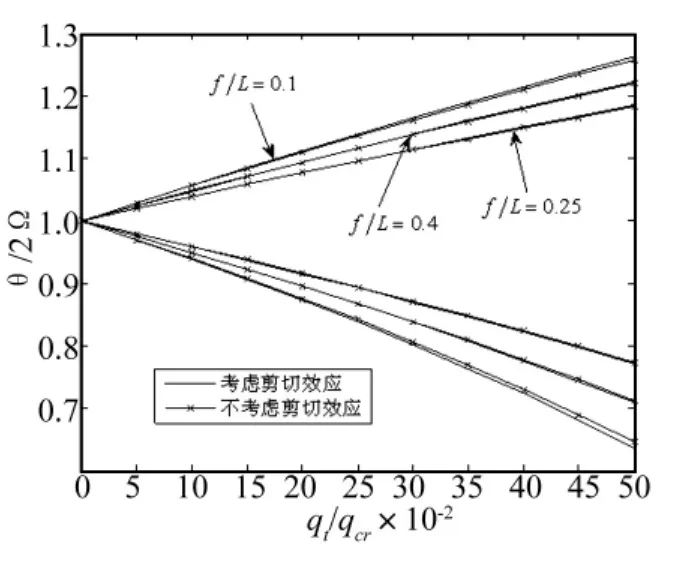
图5 随着矢跨比改变剪切变形对圆弧深拱动力不稳定区域的影响Fig.5 Effect of shear deformation with the change of rise－span ratio on principal regions of dynamic instability for circular deep arch

在长细比较小时，剪切变形对深拱的临界荷载值以及结构发生参数共振时的频率影响较大，因此对动力不稳定区域的影响比较明显，但随着长细比的增加，对动力不稳定区域的影响逐渐减小。

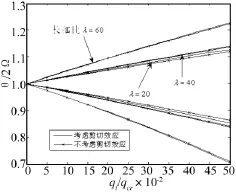
图6 随着长细比改变剪切变形对圆弧深拱动力不稳定区域的影响Fig.6 Effect of shear deformation with the change of slenderness ratio on principal regions of dynamic instability for circular deep arch

4 结论

根据能量法计算的静力临界荷载与平衡法计算的结果相同，表明本文方法是正确的。考虑剪切变形时圆弧拱弹性屈曲时的临界荷载小于不考虑剪切变形时的临界荷载。

随着圆弧半径和圆心角的增加，结构发生参数共振时的频率降低，动力不稳定区域迅速扩大，因此圆弧半径是决定拱结构动力不稳定区域的重要因素。

剪切变形不仅能减小拱弹性屈曲时的临界荷载，降低静力稳定性，同样能够增大拱发生参数共振时的动力不稳定区域，降低动力稳定性。因此对于圆弧深拱来说，无论是静力稳定问题还是动力稳定问题，剪切变形的影响都不可忽略。

［1] 鲍洛金，符 华，著.弹性体系的动力稳定性［M] .林砚田，等译.北京:高等教育出版社，1960.

［2] 王连华，易壮鹏，张 辉.周期荷载作用下几何缺陷拱的动力稳定性［J] .湖南大学学报，2007，34(11):16－19.

［3] 易壮鹏，赵跃宇，朱克兆.几何缺陷浅拱的动力稳定性分析［J] .计算力学学报，2008，25(6):932－938.

［4] Bi Q，Dai H H.Analysis of non-linear dynamics and bifurcations of a shallow arch subjected to periodic excitation with internal resonance［J] .Journal of Sound and Vibration，2000，233(4):557－571.

［5] Tien W M，Namachchivaya N S，Bajaj A K.Non-linear dynamics of a shallow arch under periodic excitation-I.1∶2 internal resonance［J] .International Journal of Non-Linear Mechanics，1994，29(3):349－366.

［6] Huang C S，Yang M C，Nieh K Y.In-plane free vibration and stability of loaded and［J] .Journal of Sound and Vibration，2000，233(4):557－571.

［7] 夏桂云，李传习，曾庆元.大曲率圆弧深拱平面弹性稳定分析［J] .工程力学，2008，25(1):145－149.

［8] 刘鸿文.高等材料力学［M] .北京:高等教育出版社，1985.