群空区危险度的结构尺寸效应灰关联神经网络模型

(中南大学 资源与安全工程学院，湖南省深部金属矿开发与灾害控制重点实验室，湖南 长沙，410083)

地下金属矿产资源的大规模开采，产生的大量采矿空区对人类和生态环境造成了严重威胁，这种群空区环境下的空区危险度状况直接影响井下矿山的安全生产[1]。目前对空区危险度的评价，常见方法有通过实际监测[2−3]或数值模拟方法[1,4−6]获得采空区周边的力学特征和形变量，与岩体的抗拉、抗压强度等参数进行比较得出评价结果，但不能快速对空区的危险度作出判定；或选择空区赋存的地质、水文条件及空区特征参数运用层次分析方法预测空区的危险度情况[7−8]。影响群空区危险度的空区尺寸、矿柱宽度、空区埋深等因素中，各自的影响程度亦具有不确定性和模糊性，很难找出确定的数学模型反映其关联程度。灰关联分析作为灰色系统的分析方法之一，能通过计算反映各因素的亲疏关系，在优化矿井通风系统、建立安全指标评价体系、综合评价煤与瓦斯突出的控制因素等案例中成功应用，取得了良好的效果[9−13]。而BP神经网络作为一种典型的大规模并行分布处理非线性信息处理系统的神经网络模型，可通过学习和存储大量的输入层−输出层映射关系并进行推理，找出输入层与输出层之间的对应关系[14]，解决了矿山安全评价、采空区地基稳定性、爆破引起的地面冲击及采空区塌陷预测等工程问题[15−18]。在矿山生产中，由于受采矿过程的影响，力学分析过程复杂，难以快速实现空区危险度的判定。但是，采空区的结构参数易于测量和管理，为适应矿山的安全生产要求，需要在分析危险度与空区结构参数的关系基础上，建立基于采空区结构参数的危险度评价，实现采矿结构参数的优化选择和安全分析。

1 加权灰关联模型

1.1 加权灰关联模型构建

灰色关联度分析是灰色系统理论的重要组成部分，其基本思路是在系统发展过程中，根据序列曲线几何形状的相似程度来判断因素间发展态势是否一致，曲线形状越相似，表明相应序列之间的关联度越大，反之就越小。对于一个系统的分析，首先要构建反应系统行为特征的数据系列，作为系统行为的映射量，用映射量间接地表征系统行为[9−10]。

设评价体系的集合X=(x1，x2，…，xn)为待评价的对象，每个对象又由m个因素指标表示其性态，Xi观测值为(xi1，xi2，…，xim)(i=1，2，…，n)，可得矩阵X=(xij)n×m[11−12]。记最佳决策方案X0的因素指标值为X0j，其值满足：

当因素指标为效益型指标时，X0j=max(x1j，x2j，…，xnj)；

当因素指标为成本型指标时，X0j=min(x1j，x2j，…，xnj)。

则将综合了最佳决策方案X0j及矩阵X所得的矩阵A=(xij)(n+1)×m称为方案集X的评价矩阵。

系统中不同因素表示的物理意义不同，使得不同的数据一般有不同的量纲，不便于比较。为满足灰色关联度分析要求，需将选择的指标进行无量纲化处理，获得可进行比较的数据列。以X0j为母因素，Xij(i=1，2，…，n；j=1，2，…，m)为子因素，对数列的所有数据均用最佳决策方案即第1列的数据X0j去除，得到A的初始化序列，即：

灰色关联系数表征各子因素与母因素的关联程度，通过下式计算可获取灰色关联度评判矩阵R。

子因素与母因素各指标的关联程度有多个，信息分散，不便于进行整体比较，需将各因素指标的关联系数集中为1个值。采用专家赋权法对待评价单元中各评价因素的权重进行赋值[11]，得加权系数W=(W1，W2，…，Wm)T，通过下式计算Xi与X0之间的加权关联度：

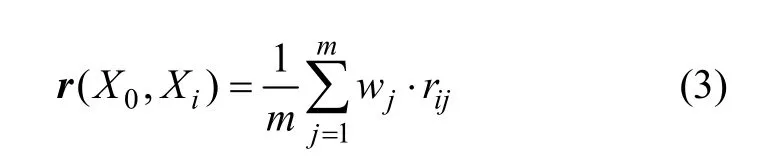
1.2 危险度灰关联分析

空区危险度是指井下大范围矿体实施空场采矿法中，由于存在大量的未处理采空区，受井下采空区的力学条件、变形特性和回采工艺的差异，使空区存在不同程度的剥离、冒顶、失稳等危险性的力学行为，通过对结构特征、力学分析等进行综合评价判定空区的危险程度，获得危险度指标和级别。按照5级的空区危险度分级方法，可以分为高危险度、较高危险度、一般危险度、较低危险度和低危险度。

空区危险度的影响因素有很多，包括空区的暴露面积、体积、埋深、相邻空区间距等，但这些指标只能对空区的危险度作出定性评价。为进行空区稳定性的定量评价，在掌握岩体力学性质的基础上，计算空区的应力、位移等，与岩体的抗拉、抗压强度等参数进行比较，综合评价空区的危险度。赛什塘铜矿经过几年的开采，井下5个中段形成了大量采空区，根据空区目前赋存情况，在前期现场 CMS空区探测的基础上，运用数值模拟软件FLAC 3D计算80个空区的最大拉应力、最大压应力及顶板最大沉降位移作为空区危险度的评价因子，并定义最大拉应力(MPa)、最大压应力(MPa)、顶板最大沉降位移(cm)的绝对值均为最大值的空区为最危险空区特征值，即X0=(−2，13.65，31.75)，建立该矿山空区危险度的评价矩阵为：

采用式(1)对A进行无量纲化处理，得矩阵A′：

由式(2)得灰色关联度评判矩阵R：

根据评价空区危险度的3个评价因子，采用专家赋权法得到加权系数：

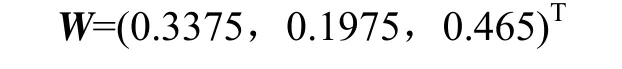
按照式(3)计算各空区与最危险空区特征值的关联度：

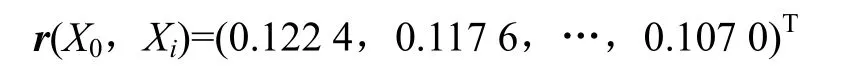
为便于比较不同空区的危险度，利用式(4)对关联度数据进行归一化处理，获得0～1范围的空区危险度，并将空区运用危险度进行分级，即：0～0.2为低危险度，0.2～0.4为较低危险度，0.4～0.6为一般危险度，0.6～0.8为较高危险度，0.8～1.0为高危险度。各空区危险度的关联度、关联序及空区的应力、位移值、危险度等级见表1。

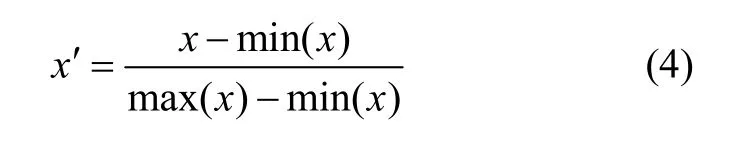
由表1可知：空区危险度越大的空区，应力、位移等力学状况也相应较差，空区越危险；而空区危险度较小的空区，应力、位移等力学状况相应较好，空区稳定性好。表明运用灰关联分析，得出各空区的危险度关联度与空区的实际危险度相符。

2 危险度灰关联神经网络模型

为通过实测的空区结构尺寸参数快速判定采空区的危险度，进而指导生产实践，建立灰关联神经网络模型，预测结构尺寸参数与空区危险度的非线性关系，从而快速判定采空区的危险度。

2.1 危险度灰关联神经网络预测模型

空区的暴露面积、高宽比、矿柱宽度和埋深4个因素中，包含了影响空区危险度的所有结构尺寸效应，如暴露面积和高宽比能够反映空区的长度、高度、宽度、体积及暴露面积。因此，选择70个空区样本，运用式(4)对暴露面积、高宽比、矿柱宽度、埋深4个因素进行归一化处理后作为输入层因子，将关联度作为模型的学习输出因子，运用神经网络软件 Easy NN-plus建立空区尺寸效应的灰关联神经网络预测模型(见图 1)。

设置学习率、惯性系数和目标训练误差的取值分别为0.6，0.8和0.01[14]，建立具有推理功能的神经网络模型，并得到表征4个输入因子对输出因子的相对重要性和相对敏感性的训练结果，分别见图2和图3。

相对重要性是输入层节点与隐含层节点连接的绝对权重值的总和，间接表明输入层节点对输出层的影响程度。由图2可知：不同的尺寸效应对空区危险度的影响度不同，相对重要性由大至小依次为矿柱宽度、暴露面积、高宽比、埋深，表明在以上4个空区危险度的影响因素中，矿柱宽度对危险度的贡献最大，埋深的贡献最小。

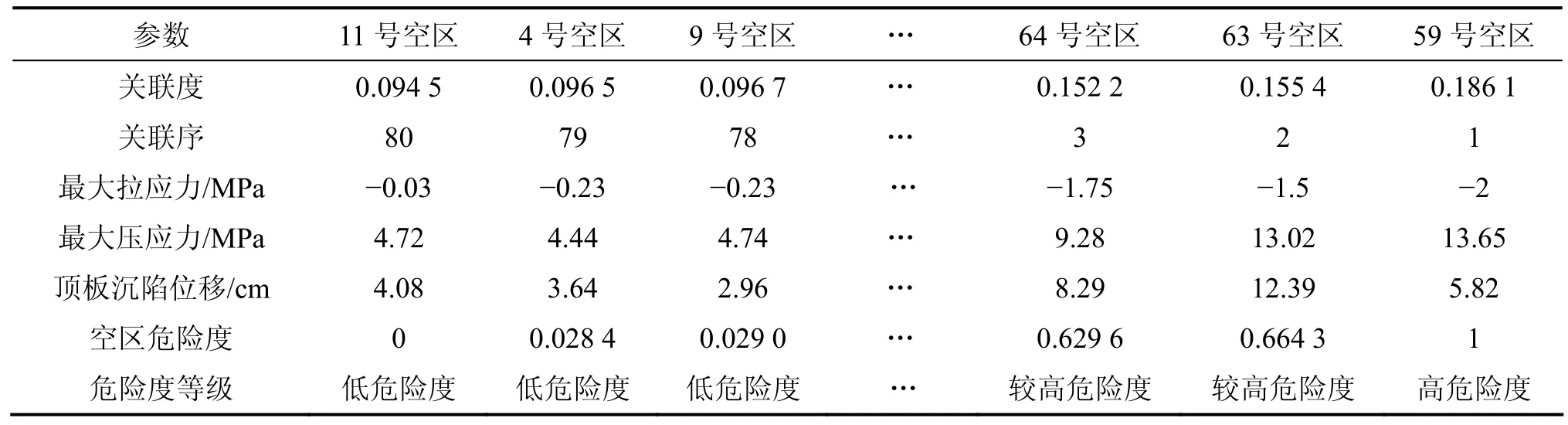
表1 空区关联度及关联序Table 1 Correlation and associated sequence of mine goafs

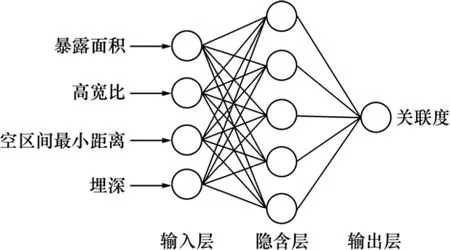
图1 神经网络预测模型Fig.1 Neural network prediction model

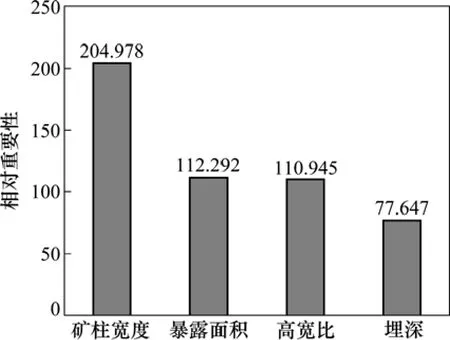
图2 影响因素的相对重要性Fig.2 Relative importance of factors

相对敏感性表征输出层节点随输入层节点的变化情况。图3所示为不同的尺寸效应对空区危险度变化的敏感度不同，相对敏感度由大至小依次为矿柱宽度、暴露面积、埋深、高宽比。

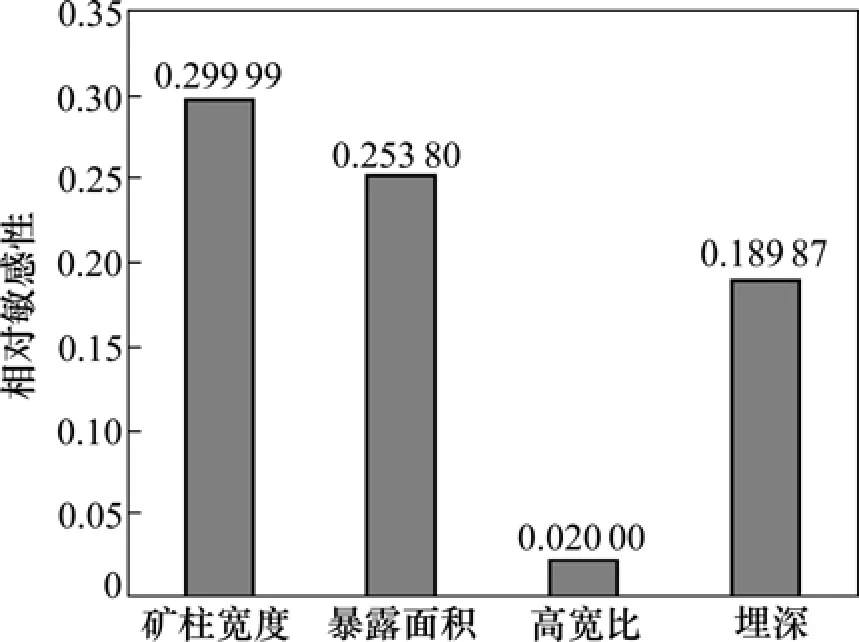
图3 影响因素的相对敏感性Fig.3 Relative sensitivity of factors

2.2 危险度神经网络预测

选择 15个空区作为预测样本，经式(4)对样本的暴露面积、高宽比、矿柱宽度和埋深4个因素进行归一化处理后，运用Easy NN-plus建立的神经网络模型预测空区危险度的关联度，并根据预测结果判定空区危险度情况，见表2。

表2所示的预测结果数据显示：基于灰关联分析结果建立的空区结构尺寸效应神经网络模型，预测误差范围为0.082 3%～6.748 3%，平均误差为3.054 6%，表明该神经网络模型能对该矿空区的危险度进行较准确预测。

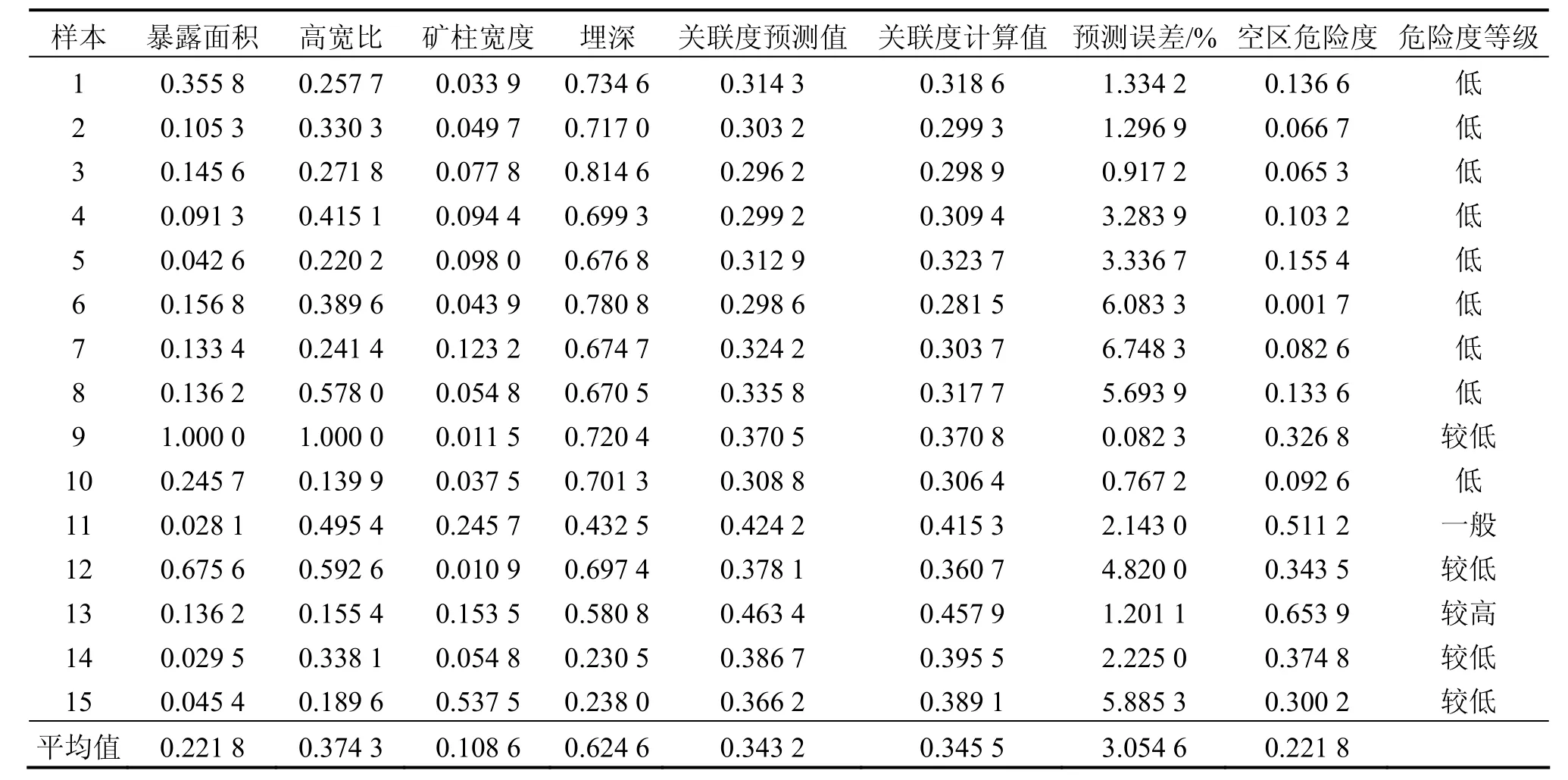
表2 预测样品的归一化参数及预测结果Table 2 Normalized parameters and prediction results of prediction samples

3 危险度结构尺寸效应

采空区的结构尺寸是影响危险度的重要因素，运用建立的结构尺寸效应灰关联神经网络模型，选取暴露面积、高宽比、矿柱宽度和埋深4个因素进行分析，选取其中1个因素指标为变量，假定其他3个因素恒定的条件下，分析空区危险度随暴露面积、高宽比、矿柱宽度、埋深的单值变化，预测结果见图4～7。

对暴露面积而言，在单一变化的条件下，由291 m2变化至4 350 m2，关联度随空区暴露面积的增大而增加，其关系近似为线性正相关，如图4所示。这是由于在矿体开挖后，空区顶板部分自重应力传递到周边未经采动的岩体，顶板岩层形成减压区，两帮围岩形成增压区，使顶板发生类似弹性恢复那样的膨胀变形，两帮围岩发生压缩变形，在其他因素不变的情况下，顶板膨胀变形以及两帮围岩压缩变形随暴露面积的增大而增大，使空区顶板所受的拉应力更大，两帮围岩所受的压应力更大，导致空区危险度增加。

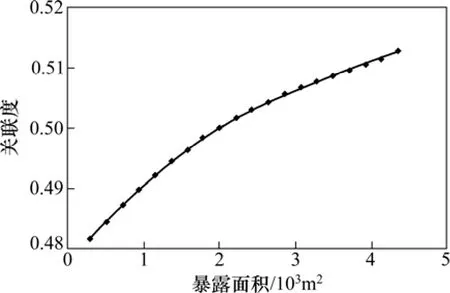
图4 关联度随暴露面积变化Fig.4 Relationship between relational degree and exposed area

由图5可知：在单一因素高宽比由1变化至2.14时，关联度随高宽比增加而急剧增加，至高宽比为2.14时，关联度达到最大值0.467 9；在高宽比由2.14变化至3.19时，关联度随高宽比增加而减小，最小减小至0.349 3；之后关联度不再随高宽比增加而变化，其值均为0.349 3。这是由于在高宽比为1的理想情况下，空区顶底板中心和两帮中点的周边应力分布比较均匀，且随着高宽比的增大，顶底板及两帮的应力分布逐渐变差，空区危险度增大；在高宽比增大到一定程度时，空区形状与受力情况越类似于巷道等线性工程，空区危险度减小并趋于稳定。

由图6可知：在单一因素矿柱宽度由1.4 m增加至8.3 m时，关联度随间距的增大显著减小，最小值为0.311；矿柱宽度大于8.3 m时，关联度不再随矿柱宽度的增大而变化。这是由于矿柱宽度即空区间间柱宽度由1.4 m增加至8.3 m时，空区间间柱的受力情况得到显著改善；而空区间间柱宽度大于8.3 m时，间柱的受力情况趋于稳定，导致关联度不再随间柱宽度的增大而变化。

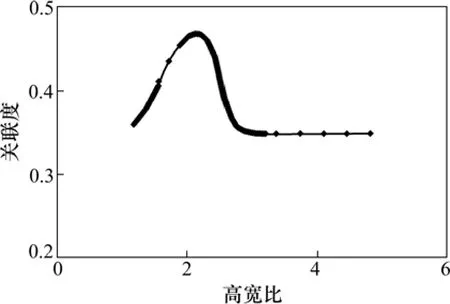
图5 关联度随高宽比变化Fig.5 Relationship between relational degree and aspect ratio

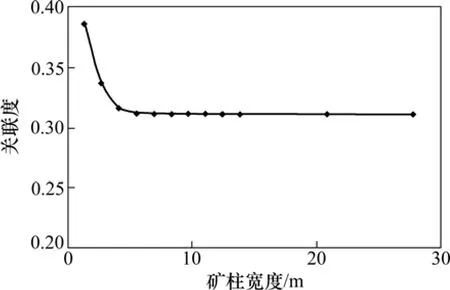
图6 关联度随矿柱宽度变化Fig.6 Relationship between relational degree and pillar width

图7 关联度随埋深变化Fig.7 Relationship between relational degree and depth

由图7可知：在单一因素埋深变化时，关联度随埋深的增加而增大，表明随着空区埋深的增加，空区危险度增加。这是由于随着空区埋深增大，上覆岩层的自重应力增大，对空区周边围岩的应力作用增大，导致空区的危险度增加。

4 结论

(1) 选择最大拉应力、最大压应力和顶板最大沉陷位移3个评价因子，建立空区危险度灰关联分析模型，通过关联度计算判定空区危险度状况，实现了 5级的危险度分级评价，其危险度与空区的实际应力、位移情况反映的危险度一致。

(2) 基于神经网络软件Easy NN-plus建立空区危险度的结构尺寸效应灰关联神经网络模型，研究了空区危险度影响因素的相对重要性，结果显示相对重要性由大至小依次为矿柱宽度、暴露面积、高宽比、埋深。对15个空区样本危险度进行神经网络预测，得出该神经网络模型的预测误差范围为 0.082 3%～6.748 3%，平均误差为3.054 6%。

(3) 在其他影响因素不变的情况下，空区的危险度与暴露面积、埋深呈正相关性，与矿柱宽度呈负相关性，而与高宽比的关系式随着高宽比增大先增大后减小并最终趋于定值。

[1] 张耀平, 曹平, 袁海平, 等. 复杂采空区稳定性数值模拟分析[J]. 采矿与安全工程学报, 2010, 27(2): 233−238.ZHANG Yao-ping, CAO Ping, YUAN Hai-ping, et al.Numerical simulation on stability of complicated goaf[J]. Journal of Mining & Safety Engineering, 2010, 27(2): 233−238.

[2] 陈颂文. 广西某矿特大采空区稳定性的监测[J]. 采矿技术,2009, 9(2): 22−23, 44.CHEN Song-wen. A large mining area stability monitoring of the mined in Guangxi[J]. Mining Technology, 2009, 9(2): 22−23,44.

[3] 尹彦波. 采空区稳定性监测预警新技术研究与应用[J]. 采矿技术, 2008, 8(5): 33−37.YIN Yan-bo. Gob stability monitoring and early warning of new technology research and application[J]. Mining Technology,2008, 8(5): 33−37.

[4] 吴亚斌. 基于CMS实测的采空区群稳定性数值模拟研究[D].长沙: 中南大学资源与安全工程学院, 2007: 1−66.WU Ya-bin. CMS-based group measured the stability of mined-out area of numerical simulation[D]. Changsha: Central South University. School of Resources and Safety Engineering,2007: 1−66.

[5] 陈庆发, 周科平, 胡建华, 等. 碎裂矿段开采与空区处理协同研究[J]. 中南大学学报: 自然科学版, 2010, 41(2): 728−735.CHEN Qing-fa, ZHOU Ke-ping, HU Jian-hua, et al. Synergism study of mining and goaf treatment in cataclastic ore section[J].Journal of Central South University: Science and Technology,2010, 41(2): 728−735.

[6] 陈赞成, 侯克鹏, 杨八九. 某矿采空区稳定性三维有限元数值模拟[J]. 有色金属, 2010, 62(3): 142−145.CHEN Zan-cheng, HOU Ke-peng, YANG Ba-jiu. 3D finite element numerical simulation on gob stability of some mine[J].Nonferrous Metals, 2010, 62(3): 142−145.

[7] 杨扬, 冯乃琦, 余珍友. 层次分析和隶属函数在采空区稳定性评价中的应用[J]. 矿冶工程, 2008, 28(5): 23−26.YANG Yang, FENG Nai-qi, YU Zhen-you. Application of AHP and fuzzy membership function in stability evaluation of mine-out areas[J]. Mining and Metallurgical Engineering, 2008,28(5): 23−26.

[8] 王新民, 谢盛青, 张钦礼, 等. 基于模糊数学综合评判的采空区稳定性分析[J]. 昆明理工大学学报: 理工版, 2010: 35(1):9−13.WANG Xin-min, XIE Sheng-qing, ZHANG Qin-li, et al.Stability analysis of mined-out area based on fuzzy mathematical comprehensive evaluation[J]. Journal of Kunming University of Science and Technology: Science and Technology, 2010, 35(1):9−13.

[9] 李中才, 刘刚. 矿井安全指标的灰色关联评价模型及应用[J].矿业工程, 2006, 4(4): 57−59.LI Zhong-cai, LIU Gang. Gray relevancy assessment model used to analyze safety-influencing indexes of underground mining[J].Mining Engineering, 2006, 4(4): 57−59.

[10] 伍爱友, 肖红飞, 王从陆, 等. 煤与瓦斯突出控制因素加权灰色关联模型的建立与应用[J]. 煤炭学报, 2005, 30(1): 58−62.WU Ai-you, XIAO Hong-fei, WANG Cong-lu, et al.Establishment and application of weights and gray association model based on coal and gas outburst controlled factors assessment[J]. Journal of China Coal Society, 2005, 30(1):58−62.

[11] 吕锋, 崔晓辉. 多目标决策灰色关联投影法及其应用[J]. 系统工程理论与理论, 2002, 22(1): 103−107.LÜ Feng, CUI Xiao-hui. Multi-criteria decision grey relation projection method and its application[J]. Systems Engineering:Theory & Practice, 2002, 22(1): 103−107.

[12] 支学艺, 江小华, 黄洪祥. 基于灰色关联投影分析的矿井通风方案优化研究[J]. 黄金, 2010, 31(3): 27−29.ZHI Xue-yi, JIANG Xiao-hua, HUANG Hong-xiang. Based on the grey relation projection method for optimization of mine ventilation system[J]. Gold, 2010, 31(3): 27−29.

[13] 曹树刚, 徐阿猛, 刘延保, 等. 基于灰色关联分析的煤矿安全综合评价[J]. 采矿与安全工程学报, 2007, 24(2): 141−145.CAO Shu-gang, XU A-meng, LIU Yan-bao, et al.Comprehensive assessment of security in coal mines based on grey relevance analysis[J]. Journal of Mining & Safety Engineering, 2007, 24(2): 141−145.

[14] 蒋复量, 周科平, 李书娜, 等. 基于粗糙集-神经网络的矿山地质环境影响评价模型及应用[J]. 中国安全科学学报, 2009,19(8): 126−132.JIANG Fu-liang, ZHOU Ke-ping, LI Shu-na, et al. Study on the model of mines’ geological environmental impact assessment based on rough set and artificial neural network and its application[J]. China Safety Science Journal(CSSJ), 2009, 19(8):126−132.

[15] 王志, 郭勇. 基于BP神经网络的非煤地下矿山安全评价模型[J]. 中国安全科学学报, 2009, 19(2): 124−128.WANG Zhi, GUO Yong. Safety assessment model of underground non-coal mine based on BP neural network[J].China Safety Science Journal(CSSJ), 2009, 19(2): 124−128.

[16] 慎乃齐, 杨建伟, 郑惜平. 基于神经网络的采空塌陷预测[J].煤田地质与勘探, 2001, 29(3): 42−44.SHEN Nai-qi, YANG Jian-wei, ZHENG Xi-ping. Prediction of mining collapse based on neural network[J]. Coal Geology &Exploration, 2001, 29(3): 42−44.

[17] YONG Lu. Underground blast induced ground shock and its modeling using artificial neural network[J]. Computers and Geotechnics, 2005, 32(3): 164−178.

[18] 丁陈建, 汪吉林. 神经网络法的采空区地基稳定性评价[J].采矿与安全工程学报, 2009, 26(2): 208−211.DING Chen-jian, WANG Ji-lin. Using artificial neural network to assess the stability of goaf foundation[J]. Journal of Mining &Safety Engineering, 2009, 26(2): 208−211.