基于“P－模糊－PI”多模控制器的热导池温度控制系统

郭稳涛，何怡刚

（1.湖南机电职业技术学院电气工程系，湖南 长沙 410151；2.湖南大学电气与信息工程学院，湖南 长沙 410082）

热导检测器（Thermal Conductivity Detector，TCD）是一种常见的气相色谱法分析仪器，它具有结构简单、性能稳定、响应速度快、线性范围宽、对无机气体和各种有机物都能做出响应等优点，同时又是非破坏性检测器，故广泛应用于化学工业和电厂的气体分析.［1］

热导检测器是利用被测气体组分或者浓度与载气的热导系数不同而做出响应的浓度型检测器，当通过热导池孔道的气体组分或者浓度发生变化时，孔道中的热敏元件向热导池壁传导的热量发生变化，从而引起热敏元件电阻值的变化.通过电桥将这种电阻值变化转化成电信号，便可以反映出气体组分或者浓度的变化.［2］本文首先分析热导池温度稳定性对热导检测器灵敏度的影响，然后设计了一种基于模糊PID控制器的热导池温度控制系统，实验结果表明，该系统有效地提高了热导池温度控制系统的响应速度和稳态精度，避免了因热导池温度的不稳定而造成的热导检测器灵敏度下降.

1 热导池温度波动对灵敏度的影响

TCD的响应是热平衡的结果，它的定量精度和稳定性主要取决于温度波动的大小.［3］当通过热导池的载气、电桥电流及池温达到恒定时，电桥电流在热敏元件上产生的热量与散失的热量相等，具体可描述为

其中：I为热敏元件上流过的电流；R为热敏元件的电阻值；J为焦耳当量；G为几何因子，是热导池孔道和热敏元件几何形状的函数；λ为气体的热导率；Tf和Tw分别为热敏元件的温度和热导池池壁的温度；θ为由热丝辐射、冷端散热等方式造成的热流失，不属于气体热导系数的响应，这里不予考虑.［4］

当被测气体进入测量臂孔道，就会引起气体热导率的变化；气体热导率的改变，引起热敏元件温度的变化；热敏元件温度的改变，引起热敏元件阻值的变化；热敏元件阻值的变化，引起测量电桥输出电信号的变化.故电桥输出是热导检测器中各个变量相继变化的结果.

（1）组分浓度X2对热导率λ的影响

设载气和被测气体的相对分子质量分别为M1和M2，其横截面积为σ1和σ2，组分浓度对热导率的

影响可近似表达为

（2）热导率λ对热敏元件温度Tf的影响

根据热导池热平衡公式（1），显然有

（3）热敏元件温度Tf对电阻值R的影响

热敏元件与其温度的关系可近似地写成

其中R0为热敏元件在0℃时的阻值，α为电阻的温度系数，单位为Ω／（Ω·℃）.那么显然有

（4）热敏元件电阻值R对电桥输出电压Eg的影响

对于检测电阻为R1与R4的双臂恒流式惠斯顿电桥检测电路，电桥的输出电压可近似的写成

当R2＝R3＝R时，可以得到热敏原件电阻变化对检测电路输出电压的影响为

根据（2），（3），（5）与（7）式，组分浓度对检测电路输出电压的影响可表述为

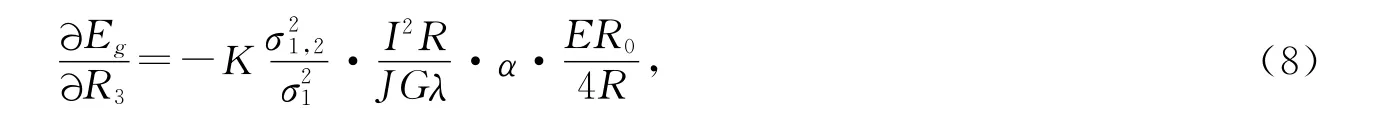
单位为 V／mol，若将输出电压换成E′g（单位：mV），质量浓度换为c（单位：mg／mL），那么（8）式可表述为通用的TCD灵敏度（单位：mV·mL／mg）

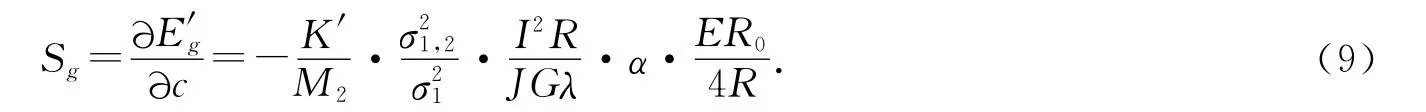
其中：K′＝5.1×104，M2为组分气体相对分子质量.再根据（1）式，Sg可表述为

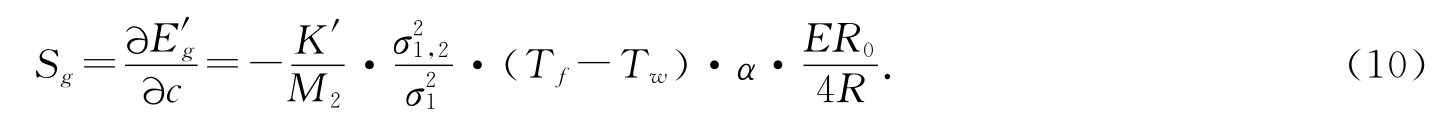
由于K′，σ1，σ2，M2和α均为常数，当电桥电压E采用10－5／℃的高精度电压基准时也可认为是常数，热敏元件在0℃时的阻值R0也是常值，那么由（10）式可知，池体温度Tw的控制精度是影响热导检测器灵敏度的唯一因素，提高热导池池体温度的控制精度是提高热导检测器灵敏度的根本方法.

2 热导池温度控制系统硬件组成

该热导池温度控制系统的硬件组成如图1所示.

图1 热导池温度控制系统硬件结构

热导池温度的检测由Pt100热敏电阻完成，检测电桥将Pt100的电阻变化转换为电压信号后经AD620仪表放大器放大50.4倍，然后通过24位A／D转换器转换为数字信号，再通过SPI总线送入32位ARM7微控制器LPC2132，程序首先对数字温度信号进行平滑滤波，然后将实际温度值与设定温度值的偏差e（t）以及偏差变换率ec（t）作为温度控制器的输入，控制器按照一定的控制规律计算出控制量PWM信号的占空比，从而调节加热元件的输出功率，实现对热导池温度的精密控制.

3 热导池温度控制系统的辨识

我们采用阶跃响应法来对热导池温度控制系统的数学模型进行辨识.［5］对系统注入占空比为100%的阶跃信号，检测到的系统响应如图2所示.

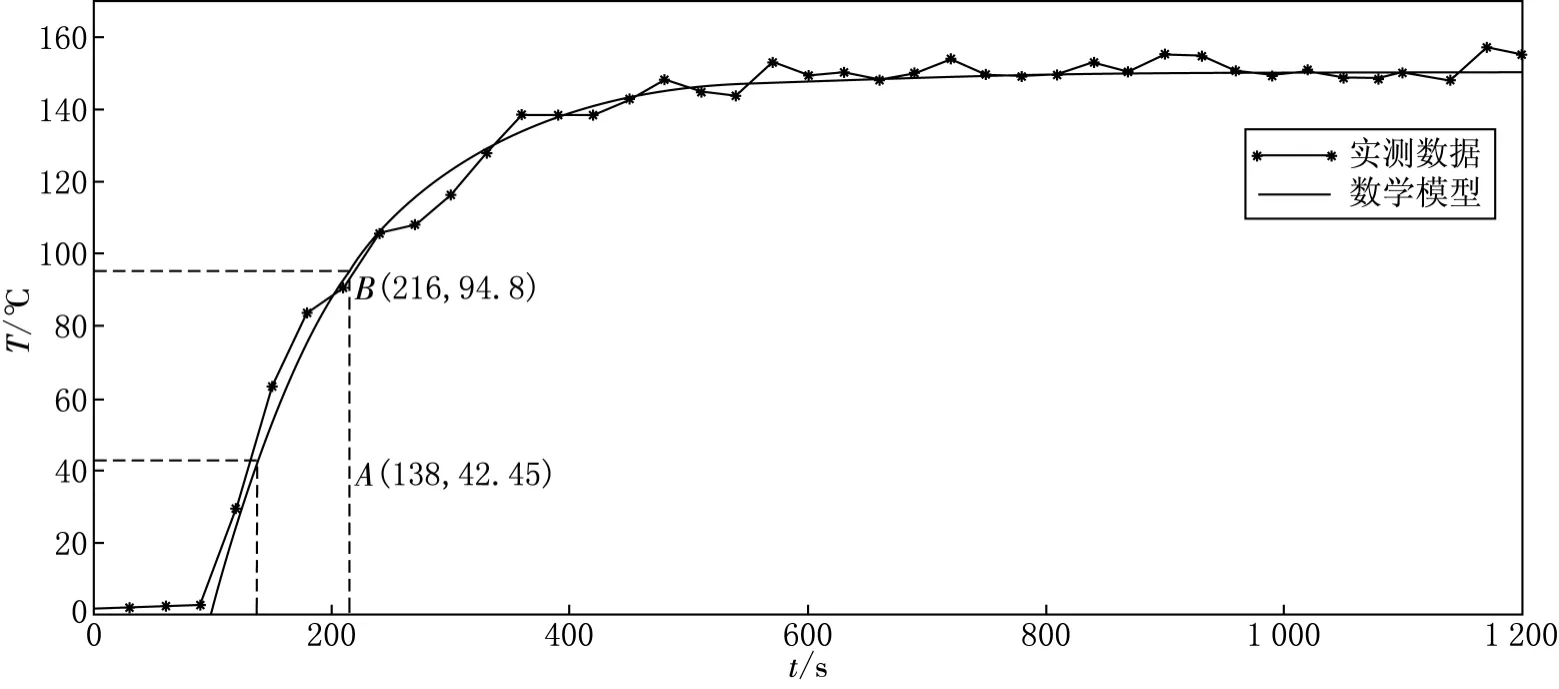
图2 热导池温度控制系统的阶跃响应

根据图2中实测数据曲线可知，热导池体温度T最高可达150℃，根据系统响应达到稳态值的28.3%和63.2%时的坐标A和B，采用一阶纯滞后数学模型来模拟热导池温度控制系统［6］，可得热导池温度控制系统的传递函数为

4 “P－模糊－PI”多模控制器设计

模糊控制器是一种模拟人类控制行为的语言控制器，它具有很强的鲁棒性和控制稳定性，尤其适用于非线性时变、滞后系统的控制.但是由于控制器不具备积分环节，因而稳态精度不高.而且在变量分级不够细的情况下，在平衡点附近会出现振荡现象.［7］PID控制器是工程中最为广泛应用的一种控制器，具有结构简单、稳定性好、稳态误差小等特点.PID控制器控制性能的优劣严格取决于控制器Kp，Ki和Kd三个参数的整定，然而工程中很难对常规PID控制的三个参数进行精确计算，尤其是对非线性、时变的复杂系统［7］.将模糊控制和PID控制结合起来就可以构成兼具两者优点的“P－模糊－PI”控制器.其构建思想是：在偏差较大的情况下，采用比例控制，以提高系统的响应速度；在偏差较小的情况下，采用模糊控制，以提高系统的阻尼性能；在偏差更小的情况下，采用PI控制，以消除稳态误差，提高系统的稳态精度，从而构成了图3所示的“P－模糊－PI”多模复合控制器.

图3 P－模糊－PI控制器框图

当｜e（t）｜≥eh时，采用P控制；当el≤｜e（t）｜＜eh时，采用模糊控制；当｜e（t）｜＜el时，采用PI控制.三种控制方式在控制过程中是分段切换使用的，不会相互影响，可以分别调试和设计，在系统的设计过程中，模糊控制器的设计和切换阈值的确定是关键.

4.1 模糊控制器的设计

借助Matlab软件提供的FIS图形化模糊控制器开发工具，模糊控制器的开发遵循以下步骤［8］：

（1）确定模糊控制器的输入变量和输出变量.这里我们选取偏差E和偏差的变化率EC作为控制器的输入变量，控制器的输出为增量式输出U.

（2）语言变量的论域设计.令E，EC和U 的论域均为｛－6，－5，－4，－3，－2，－1，0，1，2，3，4，5，6｝.语言变量的论域确定后便可根据实际的误差e（t）、误差变化率ec（t）和u（t）的范围来确定量化因子ke，kec和ku将实际连续域信号转化到有限整数离散域.由于模糊控制器仅在el≤｜e（t）｜＜eh作用，故这里可以适当减小e（t）的范围，以提高控制效果.根据实验数据，选取e（t）∈［－5，t］，那么可得ke＝1.2；选取ec（t）∈［－0.26，0.26］，那么可得kec＝23；选取控制器输出增量u（t）∈［－6，6］，那么可得ku＝1.

（3）确定各语言变量的语言值及其隶属函数.结合控制系统的复杂程度以及控制效果，将E，EC和U 划分为｛“正大（PL）”，“正中（PM）”，“正小（PS）”，“零（ZO）”，“负小（NS）”，“负中（NM）”，“负大（NL）”｝7档，均选用三角形隶属函数.

（4）创建控制规则.根据专家控制经验以及实验数据，总结出的控制规则如表1所示.

（5）确定模糊推理方法.这里选取Mamdani推理方法.

（6）清晰化接口.这里选取加权平均法.清晰化处理后得到的模糊控制器的精确输出量U，通过比例因子ku可以转化为实际作用于控制对象的控制增量.

表1 模糊控制规则表

经过反复的仿真与现场调试，不断地修改控制规则，为了便于单片机处理，利用Matlab提供的evalfis函数，生成了模糊查询表，如表2所示.

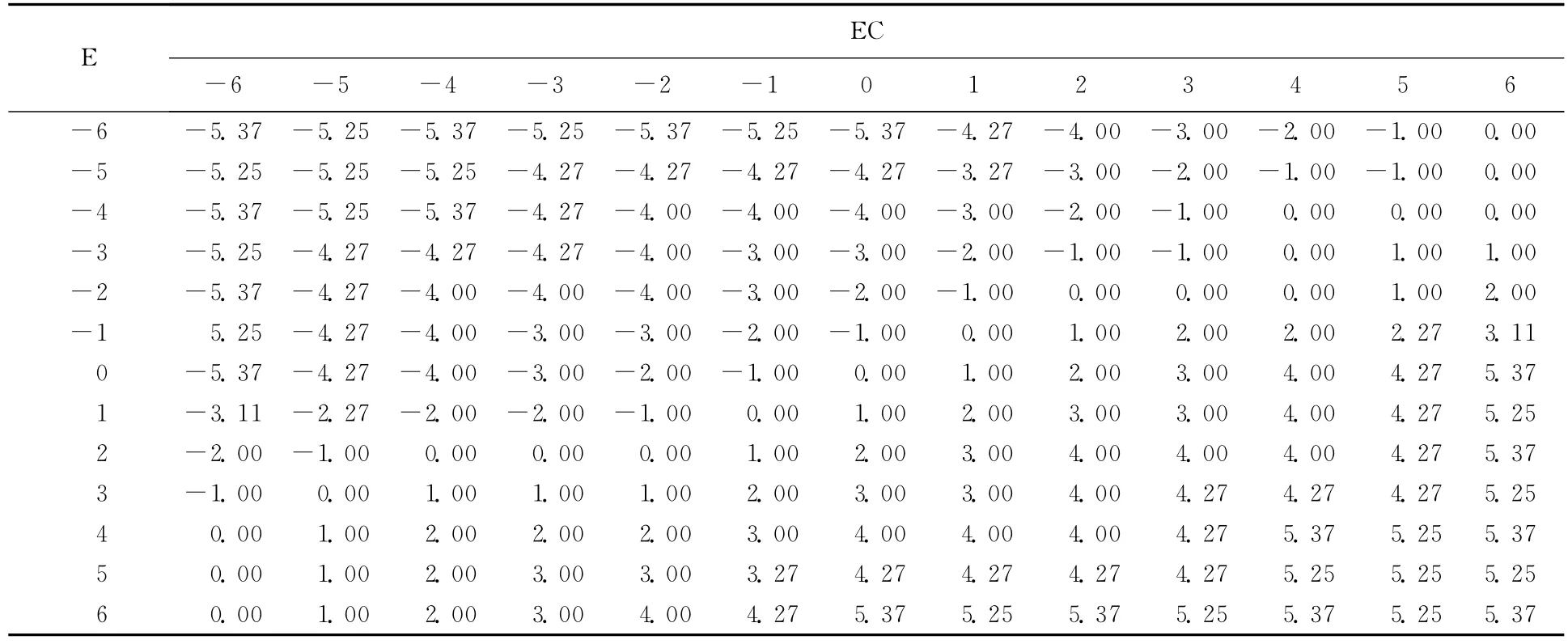
表2 模糊查询表

4.2 模式切换阈值的确定

模式切换阈值eh和el的大小对“P－模糊－PI”多模控制器的控制效果有着重要的影响.切换阈值eh决定着控制器从P控制到模糊控制的切换点，如果eh过大，那么控制器就会过早地由P控制切换到模糊控制，对控制器的响应速度造成影响；如果eh过小，控制器则有可能产生较大的超调量.切换阈值el决定着控制器从模糊控制到PI控制的切换点，如果el过大，那么PI控制会较早的进入控制过程，模糊控制器鲁棒性强的优势就难以体现；如果el过小，系统则可能出现稳态误差.

由于在设计模糊控制器时，偏差e（t）∈［－5，5］，故合理的eh应该大于5，结合实验过程中，偏差e（t）的波动范围，选取eh＝20.

在模糊控制中，当语言变量的语言值为“零（ZO）”时，实际的偏差e（t）并不一定为零，这也正是模糊控制器存在稳态误差的原因.为了消除稳态误差，当｜e（t）｜＜el时，控制器切换至PI控制，PI控制中的积分环节发挥作用以消除稳态误差.选取偏差语言变量的语言值为“零（ZO）”时切换至PI控制器，故这里e（t）＝0.83.

4.3 多模控制器的Simulink仿真

在控制器的设计过程中，为了验证模糊控制规则以及各项参数对控制器性能的影响，在Simulink软件中搭建了热导池温度控制系统的仿真模型［9］，如图4所示.

图4 仿真模型

为了比较控制器的性能，图5给出了PI控制器、模糊控制器以及“P－模糊－PI”多模控制器在设定值为100℃的响应曲线.从图5中可以看出，PI控制器响应速度较快，但超调量较大；模糊控制器响应速度较慢且存在稳态误差；“P－模糊－PI”多模控制器在响应速度、超调量以及稳态误差等方面均比较理想，可以明显看出温度上升到80℃时，由于误差小于20℃，控制器从P控制切换到模糊控制.

图5 控制效果对比

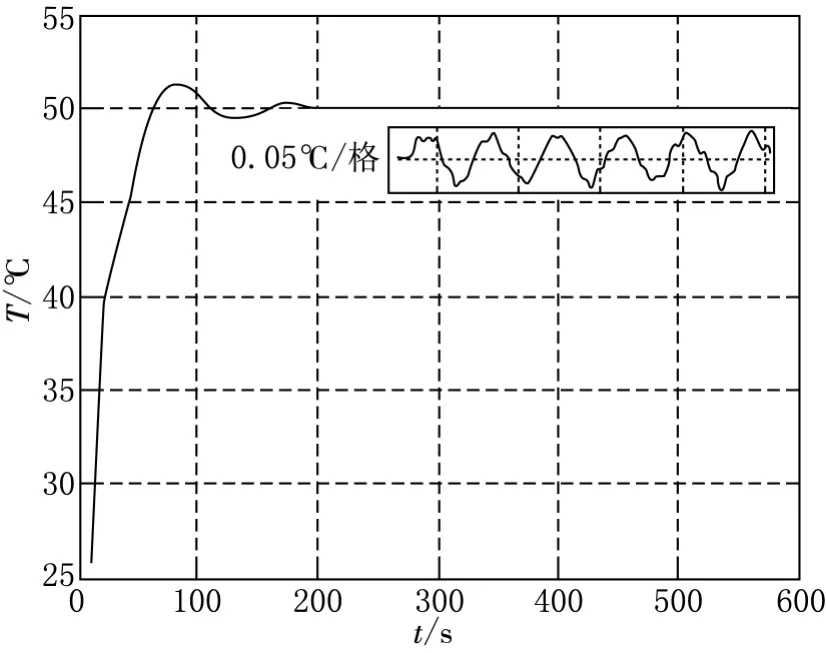
图6 温度控制曲线

5 控制效果分析

为验证温度控制系统的实际控制效果，将研制的温度控制系统装入爱尔兰AGC公司生产的GC－1803型热导池，温度采集选用福禄克8508A数字多用表，选用100ΩPRT／SPRT型探头，该探头标称电阻100Ω、标称温度0℃、测量精度0.0025℃，设定池体温度为50℃，实验记录到的10min的温度曲线如图6所示.由此图可以看出，从室温26℃左右到达稳定温度50℃时间约为200s，温度的控制精度为0.05℃.对比文献［10］提出的方法得到的温度控制精度0.1℃，文献［11］中提出的方法得到的温度控制精度0.5℃，系统预热时间15min，可见本文设计的基于“P－模糊－PI”多模热导池温度控制系统无论在上升时间还是稳态精度方面都显著优越于已有算法.

6 总结

稳定的热导池温度是保证热导检测器定量精度及稳定性的重要因素.“P－模糊－PI”多模控制器结合了比例控制、模糊控制以及PI控制的优点，具有响应速度快、超调量小、无稳态误差、鲁棒性好等特点，能为热导池温度控制系统提供可靠的控制.本文设计的热导池温度控制系统成功运行于某热导池氢气浓度变送器，温度控制精度达到了0.05℃，保障了变送器的灵敏度及稳定性.

［1］李浩春，卢佩章.气相色谱法［M］.北京：科学出版社，1998：43－45.

［2］尹立明.提高气相色谱仪分析性能探讨［J］.特钢技术，2010，16（1）：55－57.

［3］KOLESAR E S，RESTON R R.Review and summary of a silicon micro machined gas chromatography system［J］.IEEE Trans on Components，Packaging and Manufacturing Technology，1998，41（3）：324－328.

［4］LITTLEWOOD A B.Gas Chromatograph［M］.2ndedition.New York：Academic，1996：62－66.

［5］方崇智，萧德云.过程辨识［M］.北京：清华大学出版社，1987：99－102.

［6］KATSUHIKO OGATA.现代控制工程［M］.第4版.北京：电子工业出版社，2003：102－160.

［7］李世勇.模糊控制、神经控制和智能控制论［M］.哈尔滨：哈尔滨工业大学出版社，1998：254－391

［8］李丽芳，董秀娟.基于 T－S模糊模型的新型非线性系统控制器设计［J］.东北师大学报：自然科学版，2011，43（3）：54－59.

［9］薛定宇，陈阳泉.基于 Matlab／Simulink的系统仿真技术与应用［M］.北京：清华大学出版社，2002：235－323.

［10］刘京诚，靳斌，杨冠玲，等.一种智能型色谱仪温度控制器研究［J］.宇航计测技术，1999，19（3）：51－55.

［11］杨志勇，管伊春，严利民.一种热导式在线分析仪的温度控制方法［J］.仪器仪表学报，2005，26（8）：248－249.