横桥向地震作用下简支梁桥偏心碰撞反应参数研究

石 岩，王军文，李建中，艾庆华

(1.石家庄铁道大学 土木工程学院，石家庄 050043;2.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，石家庄 050043;3.同济大学 桥梁工程系，上海 200092)

在历次地震中，桥梁落梁破坏的情况时有发生。为了避免横桥向落梁等灾难性损坏或为保证支座的抗震安全性，通常在横桥向设置挡块等抗震措施。在强震作用下，桥梁上下部结构的不同相振动极易导致梁体与抗震挡块间发生碰撞。汶川大地震中，较多桥梁抗震挡块遭到严重破坏［1－2］，其中部分是由于梁体与其发生碰撞所致。目前，国内外学者对地震引起的横桥向碰撞效应进行了一些研究［3－6］，结果表明横向碰撞对结构的抗震性能有较大影响，但以上研究大都建立在对心碰撞的基础上，且假定墩柱在弹性范围内工作，而桥梁上部结构的质心与挡块质心实际上不在同一水平面上，即梁体与挡块间的碰撞属偏心碰撞，在强震作用下墩柱也往往会进入塑性区域。为此，本文根据我国梁式桥的特点，建立了考虑上部结构与挡块间偏心距、支座非线性和墩柱弹塑性的横向单墩碰撞模型，并对偏心距、碰撞刚度、初始间隙、桥墩线刚度、上部结构与盖梁质量比、上下部结构周期比及墩柱弹塑性等因素对横向碰撞效应的影响进行了参数研究。

1 横向碰撞模型

本文以城市高架桥中典型的30 m简支T梁桥为例进行横桥向地震碰撞反应分析，其中上部结构宽7.96 m，横断面由4片T梁组成，桥墩为直径1.5 m的圆柱形墩;上部结构、桥面铺装及防撞栏总重283 t，盖梁重40 t。全桥共设8块圆板式橡胶支座(GYZ325×88 mm)，单个支座的水平刚度为1.3×103kN/m。分析时将结构离散为图1所示的力学分析模型，其中m为上部结构质量，e为梁体与抗震挡块间偏心距，k为碰撞刚度，ΔG为梁体与抗震挡块间初始间隙，k0表示桥墩线刚度。c为结构碰撞阻尼，代表碰撞时的能量损失，其大小与碰撞过程中的恢复系数、接触刚度等有关［4－5］;但由于碰撞发生在极短的瞬间，所消耗的能量有限，故本文不考虑碰撞过程中的能量损失［6－7］。c0为结构阻尼，混凝土结构的阻尼比取5%，并采用瑞利阻尼。

为了考虑板式橡胶支座与墩顶和梁底接触面之间产生的滑动，采用双线性模式来模拟支座的力学特性［8］，其水平方向的恢复力模型如图2所示;F为支座所受水平方向的合力，d为支座的水平位移，k1为支座发生滑动前的刚度，k2为滑动后的刚度，Fcr为板式支座水平方向的滑动临界力。盖梁两端均设置了钢筋混凝土抗震挡块，挡块长×宽×高为200 cm×30 cm×50 cm。应用结构分析软件SAP2000进行非线性时程反应分析，墩柱采用弹塑性梁柱单元模拟，支座采用Bouc-Wen单元模拟，上部结构的质量采用集中质量代表;假定不考虑挡块与盖梁的破坏和屈服，碰撞单元采用非线性间隙单元模拟，其非线性力—位移关系为:

式中，k为碰撞刚度，ΔG为梁体与抗震挡块间初始间隙，Δd为地震作用下梁体与挡块间的横向相对位移。

表1 选用的地震波Tab.1 Selected ground motions

2 横向碰撞反应参数研究

在分析过程中，假设桥梁位于地震烈度9度区，选取表1中的10条地震波，将每条地震波的加速度峰值调整到0.4 g，沿结构横向输入。每次地震碰撞是瞬间的过程，其计算精度与时间步长有关，通过变积分步长对比分析发现:步长为0.01 s时既能保证较高的精度，又具有较高的计算效率，故本文步长取值为0.01 s。在尽量少的参数变化下，得到了桥梁结构发生横向碰撞时模型参数对碰撞反应的影响。

2.1 偏心距的影响

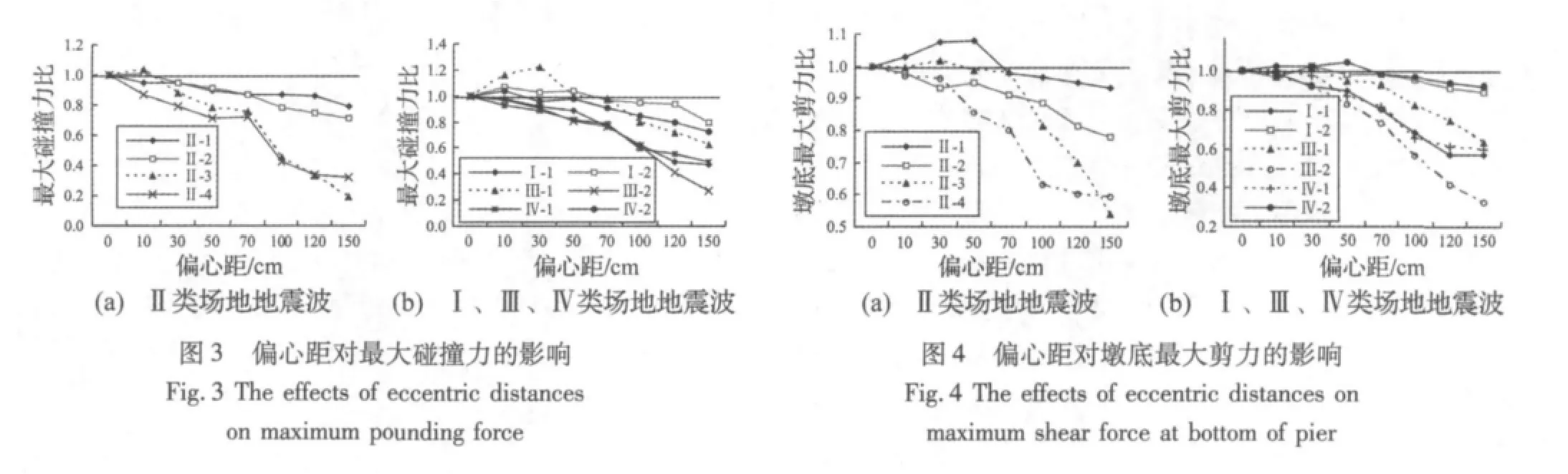
为了分析桥梁上部结构与挡块偏心距的影响，假设碰撞单元刚度5×105kN/m、初始间隙为5 cm，墩高为5 m，通过改变偏心距的大小，来考察结构地震响应随其的变化。图3为各类场地地震波作用下，不同偏心距对应的最大碰撞力比(定义为Ppi/Pd)，其中下标pi代表不同偏心距对应的地震响应量，下标d表示对心碰撞时相应的地震响应量;图4给出了各类场地地震波作用下墩底最大剪力比(定义为Vpi/Vd)随偏心距的变化关系，下标定义同前。

由图3与图4可知，考虑偏心碰撞效应时，偏心距对最大碰撞力和墩底最大剪力的影响与输入地震波的特性密切相关，输入地震动的特征周期接近于结构周期时，偏心对碰撞效应的影响更加显著。当偏心距e＜70 cm时，考虑偏心可能放大、也可能减小碰撞效应，即对于低高度梁(如空心板梁、低高度箱梁等)不考虑偏心的碰撞可能导致不保守的结果;当梁截面较高，与挡块质心的偏心距较大(e≥70 cm)时，考虑偏心减小了碰撞效应，且最大碰撞力和墩底最大剪力随偏心距的增大而减小。另外，随着偏心距的增大，计算耗时成倍增加，说明时程分析中的迭代次数明显增多，系统的非线性显著增强。

2.2 碰撞刚度的影响

目前，桥梁工程中常用的钢筋混凝土挡块，其高度相对于平面尺寸较小，抗震挡块破坏属脆性的剪切破坏［9］。汶川大地震中抗震挡块的破坏形式主要表现为:剪裂、剪断、碰撞(撞裂、撞断、撞碎)，都表现出了脆性破坏的特征。为了分析接触单元碰撞刚度对碰撞响应的影响，将碰撞刚度分为k1～k6共六个等级，根据混凝土弹性模量以及挡块的结构尺寸［5］，六个等级的碰撞刚度分别取值为5×108，5 ×107，5 ×106，5 ×105，5 ×104及5×103。碰撞单元初始间隙取5 cm，墩高为5 m，偏心距e=120 cm。经分析得出最大碰撞力与墩底最大剪力随碰撞刚度的变化如图5所示。

由图5(a)可见，在4条地震波作用下，碰撞刚度变化对碰撞力的影响非常敏感，且最大碰撞力均随碰撞刚度的增大而增大;因此，通过改变接触刚度来减小碰撞力是一种比较有效的措施，比如在间隙处设置橡胶缓冲垫［10］。从图5(b)可以看出，当碰撞刚度在5×103～5×105(kN/m)时，墩底最大剪力随着碰撞刚度的增大而单调递增，但碰撞刚度介于5×106～5×108(kN/m)时，墩底最大剪力变化波动较大，没有明显的规律。

2.3 初始间隙的影响

碰撞是一种非线性运动过程，结构在相邻构件的相对靠近位移没有达到初始间隙时，接触单元不起作用，当结构在碰撞点的相对靠近位移超过初始间隙时，接触单元被瞬时激活，结构体系中随之加入了碰撞刚度和阻尼，直到碰撞分离。在典型的El－Centro地震波作用下，Maleki［3］分析了挡块对简支梁桥地震响应的影响，发现忽略间隙会导致非常不保守甚至错误的结果。可见，初始间隙是碰撞问题中的一个重要参数。在初始间隙对横向地震反应的影响分析中，碰撞刚度取5×106kN/m，其余参数同2.2中的取值。通过改变初始间隙，得到4条地震波作用下最大撞击力和墩底最大剪力随初始间隙的变化关系，如图6所示。

由图6可知，随着初始间隙的增大，最大碰撞力和墩底最大剪力的变化波动较大，总体呈下降趋势。但文献［5］认为初始间隙是一个较不确定的影响因素。

2.4 桥墩线刚度的影响

为了适应地形等需求，通常需要设置不同高度的桥墩，桥墩线刚度随之变化。为了考察桥墩线刚度对碰撞效应的影响，以墩高12 m桥墩的线刚度i0(i0=6.73×105kN·m)为基准来改变桥墩线刚度，其余参数同2.2节。分析得到桥墩线刚度对最大碰撞力和墩底最大剪力的影响，如图7所示。

由图7可以看出，在不同地震波作用下，随着墩柱线刚度的增大，最大碰撞力的变化没有明显规律，而墩底最大剪力则单调递增，即碰撞对墩身的冲剪作用增强。因此，对于桥墩高度相差较大的桥梁，需重视碰撞作用对矮墩的冲剪破坏。

2.5 上部结构与盖梁质量比的影响

在桥梁工程中，上部结构的质量会因桥梁跨径、建筑材料(钢桥、组合结构桥、钢筋混凝土桥等)、结构形式(空心板梁、T型梁等)及铺装类型的不同而不同。为了分析上部结构与盖梁质量比对结构横向碰撞效应的影响，假定盖梁的质量mb不变，碰撞单元刚度为5×105kN/m、其余参数同2.2节。通过改变上部结构的质量ms，使上部结构与盖梁质量比α=ms/mb分别取4、5、6、7、8、9，分析质量比的变化对所考察结构响应量的影响。图8为Ⅱ类场地波作用下最大碰撞力和墩底最大剪力随质量比的变化曲线图。

由图8可知，桥梁上部结构的质量变化对结构的地震碰撞反应影响较大，随着上部结构与盖梁质量比的增大，碰撞力和墩底截面的剪力相应递增。

2.6 上、下部结构周期比的影响

分析时碰撞单元刚度取5×105kN/m，其余参数同2.2节。假设下部结构的周期 Tsub=0.11 s，通过改变上部结构的周期，使上、下部结构的周期比Tsup/Tsub分别为 6，7，8，9，10，11，12。计算出Ⅱ类场地波作用下上、下部结构周期比对最大碰撞力和墩顶位移峰值的影响如图9所示。

由图9可知，桥梁上、下部结构的周期对结构振动影响较大，上、下部结构的周期比越大，地震作用下的不同相振动趋势越明显，挡块与梁体间的碰撞力和墩顶位移越大。

图9 上、下部结构周期比的影响Fig.9 The effects of period ratio of supstructure and substructure on pounding response

2.7 墩柱弹塑性的影响

在强震作用下，桥梁结构的墩柱往往会发生屈服进入弹塑性范围。当进入弹塑性工作阶段时，墩柱存在滞回耗能，其地震响应与线弹性响应有很大不同［11］。为了分析墩柱弹塑性的影响，取碰撞刚度为5×105kN/m，其余参数同2.2节;假设塑性铰发生于墩底截面，其M－φ曲线采用UC－Fyber软件计算得到，如图10所示。不同地震波作用下，左右侧挡块的碰撞力如表2所示，图11(a)、图11(b)分别给出了Elcentro地震波作用下墩顶、梁体的横向位移时程曲线。

图10 墩柱M－φ曲线Fig.10 Moment-curvature curves of pier cross section

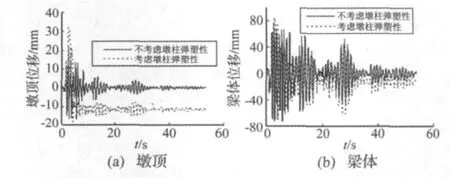
图11 横向位移时程曲线Fig.11 Time history curves of transverse displacements

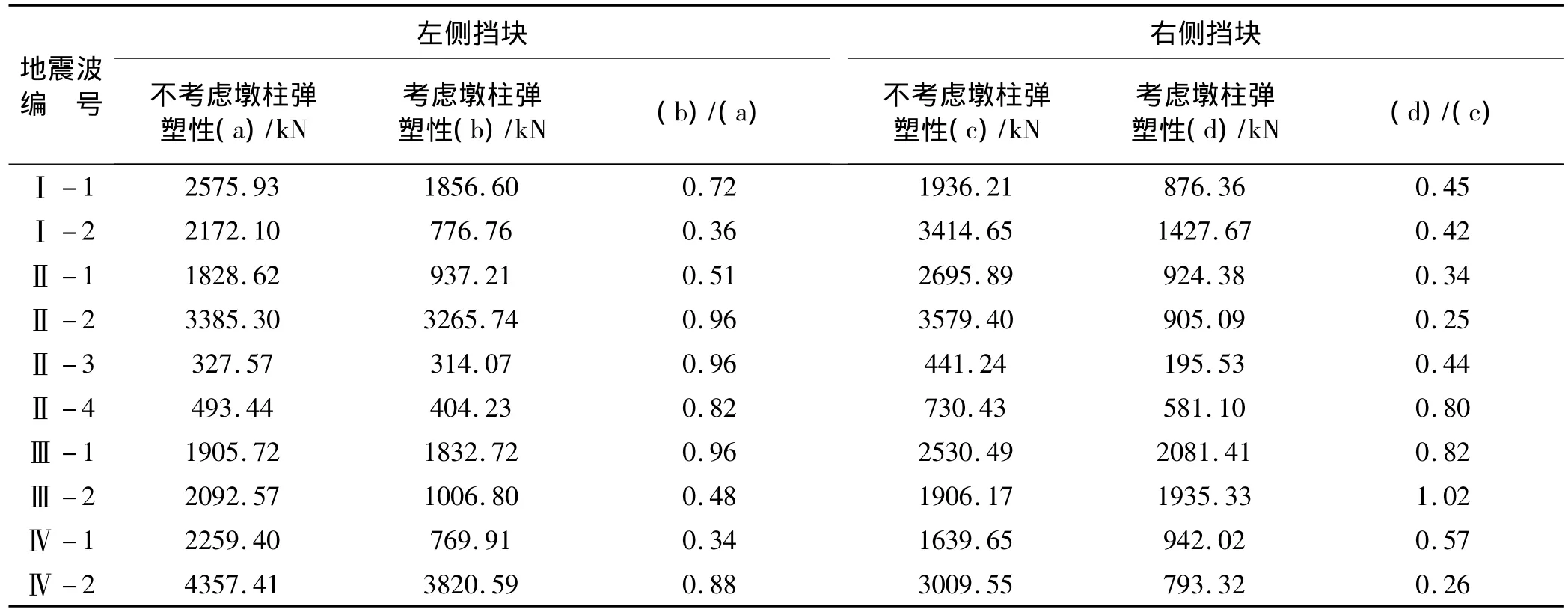
表2 左右侧挡块碰撞力Tab.2 Pounding forces of two sides shear keys

从表2可知，由于墩柱的弹塑性滞回耗能作用，挡块与梁体间的碰撞力较不考虑墩柱弹塑性时有所减小，但墩柱弹塑性对地震需求的影响程度与输入的地震动特性有关。另外，由图11可以看出，在强震作用下，考虑墩柱的弹塑性放大了墩顶位移需求，强烈的地震动导致桥墩产生了一定的残余位移。1995年日本阪神大地震中，发现一些延性桥梁因为发生了较大的残余变形，而丧失了使用功能，必须拆除重建，显示了减小残余位移的重要性［12］。因此，由于横向偏心碰撞作用导致的残余变形，应引起重视。

3 结论

本文通过横桥向单墩偏心碰撞模型分析了不同参数对简支梁桥横向碰撞反应的影响，得出以下结论:

(1)对于低高度梁(e＜70 cm)，考虑偏心可能放大也可能减小碰撞效应，故不考虑偏心的碰撞可能导致不保守的结果;当梁截面较高(e≥70 cm)时，考虑偏心减小了碰撞效应，且最大碰撞力随着偏心距离的增大而减小。

(2)碰撞刚度变化对碰撞力的影响非常敏感，碰撞力随着碰撞刚度的增大而递增，可通过设置橡胶垫等措施减小碰撞力;当碰撞刚度在5×103～5×105(kN/m)时，墩底最大剪力随着碰撞刚度的增大而递增，但碰撞刚度介于5×106～5×108(kN/m)时，墩底最大剪力的变化波动较大。

(3)初始间隙对结构碰撞效应的影响程度因输入地震动的特性而变化，随着初始间隙的增大，碰撞效应总体呈下降趋势。

(4)碰撞对桥墩的冲剪作用与其自身刚度有关，对于线刚度较大的矮墩，需重视碰撞引起的冲剪破坏。

(5)随着上部结构与盖梁质量比的增大，碰撞力和墩底剪力相应增大;桥梁上、下部结构的周期对结构振动影响较大，挡块与梁体间的碰撞力和墩顶位移随着周期比的增大而递增。

(6)考虑墩柱弹塑性反应后，挡块与梁体间的碰撞效应有所减小，而强烈的地震动会导致桥墩产生一定的残余位移，应引起重视。

［1］ 熊文林，蔡向阳.汶川大地震棉广高速桥梁震害分析［J］.华中科技大学学报，2009，26(1):119－122.XIONG Wen-lin，CAI Xiang-yang.Damage analysis of mianguang highway bridges in Wenchuan earthquake［J］.Journal of HUST.Urban Science Edition，2009，26(1):119－122.

［2］ 庄卫林，刘振宇，蒋劲松.汶川大地震公路桥梁震害分析及对策［J］.岩石力学与工程学报，2009，28(7):1377－1387.ZHUANG Wei-lin， LIU Zhen-yu， JIANG Jin-song.Earthquake-induced damage analysis of highway bridges in Wenchuan earthquake and countermeasures［J］.Journal of Rock Mechanics and Engineering，2009，28(7):1377－1387.

［3］ Maleki S.Effect of side retainers on seismic response of bridges with elastomeric bearings［J］.Journal of Bridge Engineering，2004，9(1):95－100.

［4］ 聂利英，李建中，范立础.地震作用下结构碰撞的模型参数及其影响分析［J］.工程力学，2005，22(5):143－146.NIE Li-ying， LI Jian-zhong， FAN Li-chu. Selection of Pounding Analysis parameters and its effects on structure under earth-quake ［J］. EngineeringMechanics，2005，22(5):143－146.

［5］ 邓育林，彭天波，李建中.地震作用下桥梁结构横向碰撞模型及参数分析［J］.振动与冲击，2007，26(9):104－107.DENG Yu-lin，PENG Tian-bo，LI Jian-zhong. Pounding model of bridge structures and parameter analysis under transverse earthquakes［J］.Journal of Vibration and Shock，2007，26(9):104－107.

［6］ 徐略勤，李建中，吴陶晶.碰撞效应对非规则梁桥横向地震反应的影响［J］.振动与冲击，2011，30(4):95－99.XU Lue-qin，LI Jian-zhong，WU Tao-jing.Influence of pounding effects on transverse seismic response ofa nonstandard girder bridge［J］.Journal of Vibration and Shock，2011，30(4):95－99.

［7］ 谢 旭，高博青，吴善幸，等.柔性橡胶支座上的桥梁结构地震碰撞响应分析［J］.浙江大学学报，2004，38(6):725－730.XIE Xu，GAO Bo-qing，WU Shan-xing.Earthquake response of bridges bearing on flexible rubber considering pounding of girders［J］.Journal of Zhejiang University，2004，38(6):725－730.

［8］ 范立础，聂利英，李建中.地震作用下板式橡胶支座滑动的动力性能分析［J］.中国公路学报，2003，16(4):30－35.FAN Li-chu， NIE Li-ying， LIJian-zhong. Dynamic characteristic analysis of laminated rubber bearing sliding under earthquake［J］.China Journal of Highway and Transport，2003，16(4):30－35.

［9］ 聂利英.桥梁抗震非线性分析理论研究［D］.上海:同济大学，2002.

［10］ 王军文，李建中，范立础.非规则梁桥横桥向地震碰撞反应分析［J］.振动与冲击，2010，29(6):25－30.WANG Jun-wen，LI Jian-zhong，FAN Li-chu.Analysis of pounding effect of irregular girder bridges under transverse earthquake［J］.Journal of Vibration and Shock，2010，29(6):25－30.

［11］ 王军文，李建中，范立础.连续梁桥纵向地震碰撞反应参数研究［J］.中国公路学报，2005，18(4):42－47.WANG Jun-wen，LI Jian-zhong，FAN Li-chu.Parametric study of longitudinal seismic pounding response for continuous girder bridges［J］.China Journal of Highway and Transport，2005，18(4):42－47.

［12］ Kawashima K.Seismic design and retrofit of bridges［C］.Auckland:Proc.of 12th World Conference on Earthquake Engineering，2000.