一种双耳听觉模型及其在轴心轨迹分析中的应用
李允公,戴 丽,张金萍
(1.东北大学 机械工程与自动化学院,沈阳 110819;2.沈阳化工大学 机械工程学院,沈阳 110142)
听觉模型[1-3]是一种以模拟人类听觉系统的生理结构和工作机理为主要特征的信号分析系统,除了语音、噪声、音乐、声纳等信号外,它对机械振动信号也具有良好的分析性能[4-5]。通常情况下,使用最多的是单耳听觉模型,而人类拥有的是双耳听觉系统,因此,可以考虑建立并应用双耳听觉模型。目前的听觉生理学研究表明,听觉系统对双耳耳蜗输出的信息所进行的操作主要是提取时间差ITD和强度差IID,并依据ITD和IID估计声源方位角和距离[6]。因此,建立双耳听觉模型的直接目的是进行声源定位,如Roman等[6]所建的双耳听觉模型以ITD和IID为线索,可实现声源数目的自动探测和运动轨迹跟踪。但由于信号传播方式的不同,对于机械振动信号,仅利用ITD和IID信息进行信号源的定位显然存在困难。
另一方面,听觉系统实现声源定位的过程也是一种对信号进行特征提取的过程,且特征提取的结果同声源信号的结构和声源的方位密切相关。所以,可以考虑利用双耳听觉模型对两个传感器所得信号进行处理,以实现信号的特征提取。
轴心轨迹是一种十分典型的基于双传感器的设备信息,且决定轴心轨迹形状的两个根本因素即是两路信号中相同频率成分的相位和幅值关系,因此,以轴心轨迹为分析对象,本文建立了一种双耳听觉模型,并通过试验验证了所建模型对于轴心轨迹的特征提取具有良好的性能。
1 模型的基本原理
本文所建的双耳听觉模型如图1所示。两个单耳模型的结构相同,均包括基底膜模型、内毛细胞模型和侧抑制模块,双耳模型对两侧抑制处的输出信号计算ITD和IID。其中,基底膜模型的主要功能是对信号进行带通滤波,内毛细胞模型负责对带通滤波结果进行半波整流,侧抑制模块模拟的是传入神经系统的部分功能,可对内毛细胞模型的输出信息进行频域上的精简。

图1 双耳听觉模型基本结构Fig.1 Structure of the binaural auditory model
2 模型的具体实现
2.1 基底膜模型
基底膜是人耳耳蜗的核心部件,不同频率的信号会在基底膜不同位置处激发出振动波峰,因此,通常使用Gammatone带通滤波器组[7]模拟基底膜的工作。设滤波器个数为M,第m个滤波器为h(m,t),则基底膜模型的输出为:

式中,x(t)为输入信号,y(m,t)为基底膜输出,*表示时域卷积。Gammatone滤波器的时域表达式为:

式中,α为滤波器阶数,当α=4时可以很好的模拟基底膜特性;fm为中心频率,各滤波器的中心频率在频率轴上呈对数均匀分布;相位φm通常取为零;B的计算公式为:
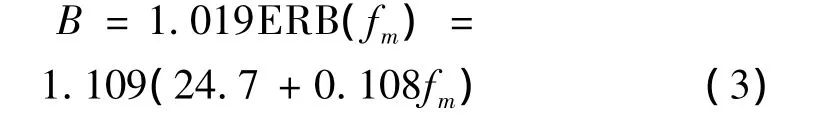
其中,ERB(fm)为滤波器的等价矩形带宽。图2为采样频率1 000 Hz,M=18时的各滤波器幅值谱的分布情况,其中横纵坐标均为对数坐标。可见,Gammatone滤波器组的各中心频率的分布随频率的升高而逐渐变得稀疏,且各滤波器之间存在较大的频率重合度,可有效避免信息的遗漏。同时易知,提高M有益于增加高频段的中心频率分布密度,但同时也加大了低频段的密度,从而使滤波信息过度冗余,因此,M不易过大。在语音信号分析中,M一般为20~190[8],考虑到机械振动信号的采样频率往往远小于语音信号的采样频率,结合以往研究经验,M取16~120较为适宜。

图2 M=18时的Gammatone滤波器组幅值谱Fig.2 Amplitude spectrums of Gammatone filterbank with M=18

2.2 内毛细胞模型
基底膜的振动会刺激耳蜗柯蒂氏器官中的内毛细胞,由其完成振动刺激到电刺激的能量转换。
内毛细胞的一个特性是只对基底膜正方向的运动产生反应,因此,本文中的内毛细胞模型负责对基底膜输出信号y(m,t)进行半波整流,即:
在后面的计算中可发现,利用半波整流后的信号进行ITD信息提取时会方便很多。同时,需要说明的是,内毛细胞还有非线性压缩和低频锁相等功能,但考虑到本文模型的具体要求,未进行模拟。
2.3 侧抑制
内毛细胞的输出信息需经过三级传入神经被传至听觉中枢,在一些听觉模型中,常使用侧抑制[9]计算简单模拟传入神经,计算方法如下:

式中:k=1,…,M-1,fk+1和fk分别为第k+1和第k个Gammatone滤波器的中心频率。式(5)实质上是对内毛细胞的输出进行频域微分,目的是消除Gammatone滤波器组较大的重合度对分析结果的影响,从而既可简化输出信息,又能够突出幅值较大的滤波信号。
考虑到计算时差的方便,对y2(k,t)再进行一次半波整流,结果设为y3(k,t)。
2.4 时差与强度差计算
设两单耳模型的侧抑制输出分别为y3L(k,t)和y3R(k,t)。由于人耳对声音信号是分段式处理的(每段约 20 ms),所以,首先将 y3L(k,t)和 y3R(k,t)等分为 N段,每一段信号设为),时域离散形式设为),L 为每段的长度。继而便可计算时差ITD和强度差IID。
目前已有的双耳听觉模型中,通常使用互相关方法计算双耳时差ITD[6],但对计算结果还需进一步判断超前还是滞后。考虑到信号经内毛细胞模型的半波整流处理后,侧抑制的输出y3(k,t)中会存在间歇式出现的幅值为零的时间段,且y3(k,t)经N等分后,每一段信号的长度较短,因此,本文采用如下的简单的数值方法得到时差ITD。
设第k个通道的第n个时间段上的时差为ITD(k,n),确定出中第一个由零变为非零的点的位置 zL(k,n)和 zR(k,n),则有:第k个通道的第n个时间段上的双耳强度差IID(k,n)则按下式计算:

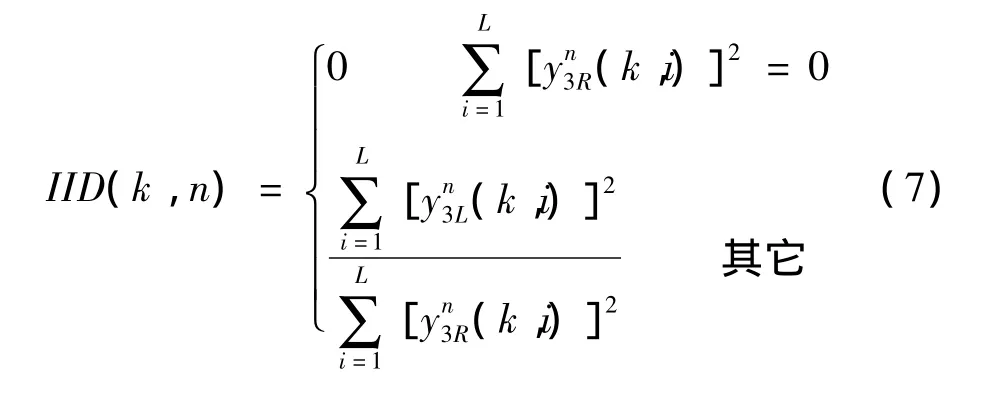
实际轴心轨迹不可能是一条理想的封闭曲线,加之在计算时差和强度差时所进行的分段处理未考虑到信号的自身状态,因此,在本文的多次试验中发现由所建模型得到的ITD(k,n)和IID(k,n)均会随时间进行波动,其中ITD(k,n)的波动更大,但其峰值几乎保持不变。由于通常在设备稳速情况下检测轴心轨迹,因此,选取第k个通道上所有时间段上ITD(k,n)的峰值ITDm(k)和IID(k,n)的均值IIDm(k)作为模型的输出。为缩减输出数据量,若某一通道所得的ITDm(k)为零,则将其略去,并同时略去该通道所得的IIDm(k)。可知,只要两路信号在某Gammatone滤波器的频段内存在初始相位不同的分量,就会得到时差和强度差的计算结果。
3 试验验证
利用一转子试验台(图3)测取五种不同形状的轴心轨迹,如图4所示,测试时采样频率为1 000 Hz,各轴心轨迹的数据点为20 000个。

图3 转子试验台Fig.3 Rotor test-bed

对于双耳听觉模型,取基底膜的Gammatone滤波器个数为48,考虑到前9个滤波器的中心频率在0~3 Hz间密集分布,故而略去,则实际的滤波器个数为39。计算时差和强度差时,取每段的长度为L=250。由各轴心轨迹得到的ITDm(k)和IIDm(k)如图5所示。
由图5可见,不同形状的轴心轨迹会得到截然不同的ITDm(k)和IIDm(k),且所使用的数据量至多只有39个点,说明本文所建模型对于轴心轨迹的特征提取具有一定的效果。在进行轴心轨迹的智能识别时,可将滤波器中心频率、ITDm(k)和IIDm(k)构成的向量作为特征,也可将ITDm(k)和IIDm(k)的某种统计结果作为特征,继而利用诸如神经网络、模糊聚类等方法进行识别和分类。当然,具体的识别方法还应结合轴心轨迹和本文模型的输出形式进行设计和研究。而无论采用哪种识别方法,所需的特征至多为30余个向量,且具有一定的信息冗余性。当然,特征的数据量还取决于Gammatone滤波器的个数。
当然,由于信号在听觉模型中经过半波整流和侧抑制处理,加之Gammatone滤波器间具有较大的重合合度,所以模型输出的ITDm(k)和IIDm(k)是两路信号在各频段上的一种统计特征,且与真实的时间差和相位差并不完全等同。

图6 图4(e)轴心轨迹两路信号的幅值谱Fig.6 Amplitude spectrums of two-channel signals in fig.4(e)
在2.4节已经提到,只要两路信号中存在初始相位不同的频率成分,就会得到相应的 ITDm(k)和IIDm(k),而且,两路信号间的时间差和强度差的大小与各单路信号的幅值间不存直接的联系,因此,信号中微弱的频率成分可能会在ITDm(k)和IIDm(k)中得到反映。如由图5(e)所示轴心轨迹得到的ITDm(k)和IIDm(k)表明,信号在120~280 Hz的频率区间内存在谐波分量,但这部分信号在两路信号的幅值谱中却十分微弱,如图6所示。所以,双耳听觉模型具有一定的提取微弱信号的潜力。同时,需要说明的是,对是否存在微弱信号成分的判断方法是某一频段中是否计算得到ITDm(k)和IIDm(k),而不是依据ITDm(k)和 IIDm(k)的幅值大小。
4 结论
模拟人类听觉系统的工作机理,建立了一种双耳听觉模型,该模型的主要目的是提取两路信号在各频段上的时间差和强度差,以实现对信号的特征提取。基于所建模型,分析了五种不同形状的轴心轨迹,所得结果具有良好的可区分性,说明双耳听觉模型对于轴心轨迹的特征提取问题具有一定的适用性。同时,由于所建模型提取的是两路信号间在强度和时间方面的关系,与单路信号的幅值无直接联系,因此,双耳听觉模型也具有表征和提取微弱信号的潜力。
[1] Serajul H,Roberto T,Anthony Z.A temporal auditory model with adaptation for automatic speech recognition[J].ICASSP’2007,2007,4:1141-1144.
[2] Klapuri A.Multipitch analysis of polyphonic music and speech signals using an auditory model[J].IEEE Transactions on Speech and Audio Processing,2008,16(2):255-266.
[3] Chu W,Champagne B.A simplified early auditory model with application in speech/music classification[C] //IEEE CCECE/CCGEI,Ottawa,2006:775-778.
[4] Li Y G,Zhang J P,Dal L,et al.Auditory-model-based feature extraction method for mechanical faults diagnosis[J].Chinese Journal of Mechanical Engineering,2010,21(3):391-397.
[5] 李允公,张金萍,高洪波,等.机械振动信号的听觉谱表达及其特性研究[J].振动与冲击,2010,29(11):204-208.
[6] Roman N,Wang D L.Binaural tracking of multiple moving sources[J]. IEEE Transactions on Audio,Speech,and Language Processing,2008,16(4):728-739.
[7] 陈世雄,宫 琴,金慧君.用Gammatone滤波器组仿真人耳基底膜的特性[J].清华大学学报(自然科学版),2008,46(6):33-38.
[8] 李朝晖,迟惠生.听觉外周计算模型研究进展[J].声学学报,2006,31(5):449-465.
[9] Wang K.Shamma S.Self-normalization and noise-robustness in early auditory representations[J].IEEE Transactions on Speech and Audio Processing,1994,2(3):421-435.

