一类非线性Jerk方程的改进两变量展开法

郑敏毅，张 农，孙光永

(湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082)

非线性Jerk方程是位移具有三阶导数含有三次非线性项的微分方程。该方程可以描述一些非线性物理问题，例如:三阶力学振子模型[1]。近来已有很多学者对非线性Jerk方程的近似周期解的研究非常感兴趣[2－6]。Gottlieb[2]用低阶谐波平衡法探讨了非线性Jerk方程的近似周期解，但是得到的低阶近似解在参数比较大时精度不高。我们很难通过谐波平衡法得到非线性Jerk方程的高阶近似解，这是由于用谐波平衡法求解Jerk方程的高阶近似解过程中需要计算非常复杂的非线性代数方程组。Wu等[3]利用牛顿谐波平衡法分析非线性Jerk方程得到了高阶近似解，得到的高阶近似解在大参数情况下精度也比较高。Ma等[4]应用同伦摄动法求解非线性Jerk方程得到的高阶近似解比低阶谐波平衡得到的近似解的精度高。Hu等[5－6]分别应用摄动法和改进的Mickens迭代法分析了非线性Jerk方程，其中高阶近似角频率是利用牛顿法求解非线性代数频率方程得到。多尺度法[7－11]是求解非线性振动问题的一种重要方法，一般经典的多尺度法对弱非线性问题的求解比较有效。Thomson[12]和Awrejcewicz等[13]用Krylov方法将摄动法推广到处理不含线性恢复力的非线性振动问题。为了使多尺度法适用于强非线性振动问题，Pakdemirli等[14]将 Lindstedt-Poincare方法与多尺度法结合提出了改进的多尺度法并成功的运用于二阶非线性振动问题的求解;Hu等[15]将Lindstedt-Poincare方法与两变量展开法结合提出改进的两变量展开法，改进的两变量展开法和改进的多尺度法的求解效果相同，但计算同一个问题时前者的计算量要小一些。本文将应用改进的两变量展开法求解非线性Jerk方程的高阶近似解。

1 改进的两变量展开法

由文献[2]可知，含有三次非线性项Jerk方程的一般形式为:

其中:参数 γ，α，β，δ，ε和a0是常数。这里的β，δ和ε至少有一个是非零。如果ε=0，则要求δ≠－2α，这是为了使Jerk方程不能简化成加速度对时间求导的方程。将方程(1)改写为:

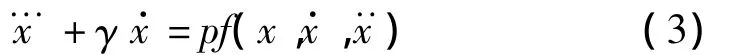
其中:p为嵌入参数表示方程(1)右边的三次非线性项函数。引入两个时间尺度:

对时间t的各阶导数可以表示成:

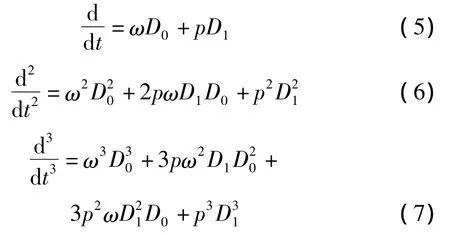
其中:D0表示，D1表示用 Lindstedt-Poincare方法将方程(3)的周期解和角频率用p的幂级数形式表示:

或:

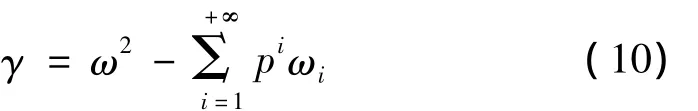
其中:ωi为待定参数。将式(8)和式(10)代入方程(3)和初始条件(2)，比较方程两边p的同次幂系数可以得到以下线性偏微分方程组和相应的初始条件

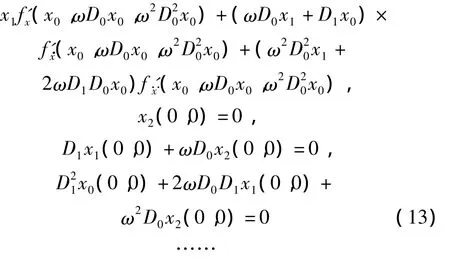
依次求解以上的线性偏微分方程组，通过消除长期项将逐次待定常数ωi，从而可以依次计算xi(η，ξ)。

2 算例

不失一般性，考虑α=ε=1，β=δ=γ=0时，方程(1)变成以下方程:

线性偏微分方程组(11)～(13)变成:

方程(15)的解为:

其中:cc表示前面项的共轭复数。将式(18)代入方程(16)化简得到:

消除长期项要求:

则:

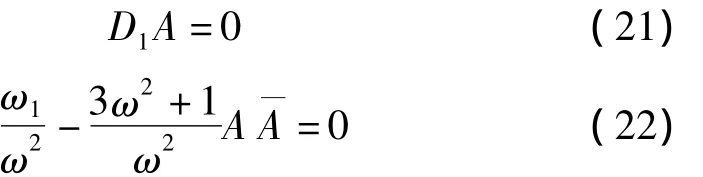
从方程(21)可知A为常数，考虑x0满足的初始条件可得:

将式(23)代入方程(22)，则:

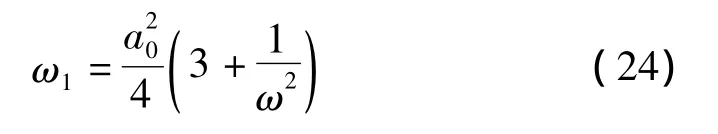
将式(23)代入式(18)得:

方程(19)的解为:

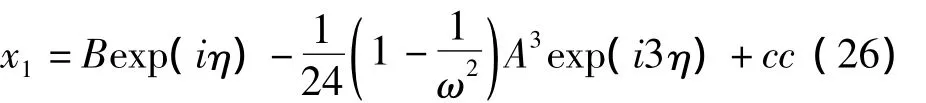
将式(18)和(26)代入方程(17)化简得:

消除长期项要求

则:

从方程(29)可知 B为常数，考虑x1满足的初始条件可得:

将式(23)和(31)代入方程(30)求解ω2得:

将式(23)和(32)代入式(26)，x1的表达式为:

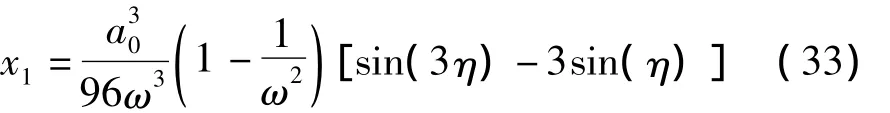
则方程(27)的解为:

其中:

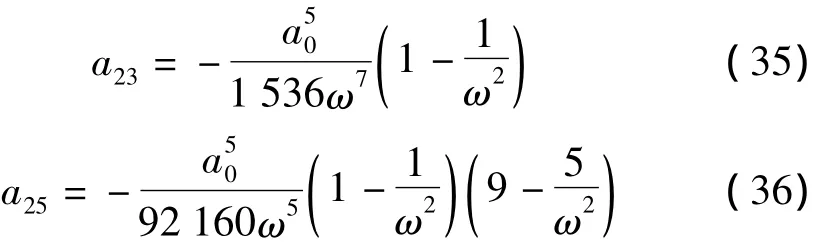
将x0，x1和x2代入三阶方程可以确定C为常数，考虑x2满足的初始条件可得:

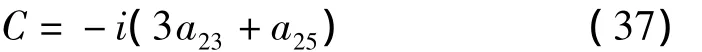
将式(37)代入式(34)得:

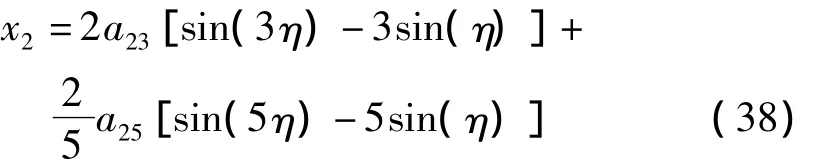
令嵌入参数p=1，则方程(14)的一阶近似周期解xa1(t)为:

其中角频率ω由以下方程给出:

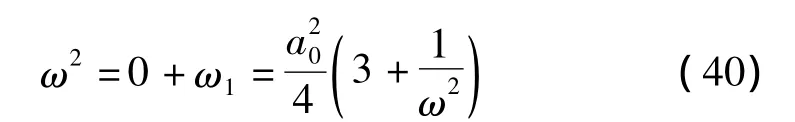
将方程两边同乘以ω2，则方程(40)变成:

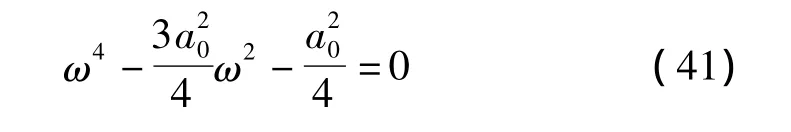
求解方程(41)得到ω2的正根为:

一阶近似角频率 ωa1为:

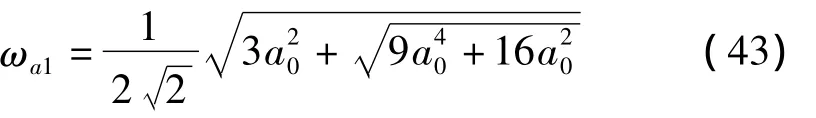
由式(43)给出的一阶近似角频率表达式与谐波平衡法[2－3]、摄动法[4－5]和迭代法[6]得到的一阶近似角频率表达式一致。其相应的一阶近似周期Ta1为:

用同样的方法可以得到方程(14)的二阶近似周期解为:

其中频率ω由以下方程确定:

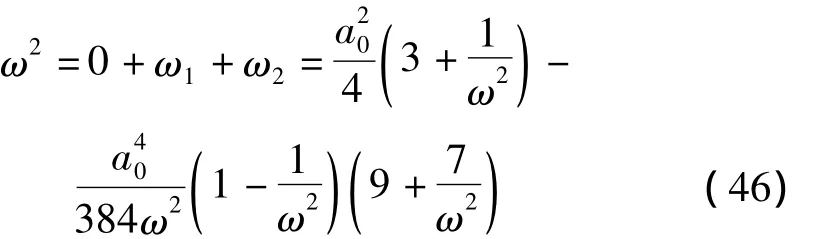
整理方程(46)得:

利用牛顿法将方程(47)线性化，将ω2看作加上一个修正项Δ，即:

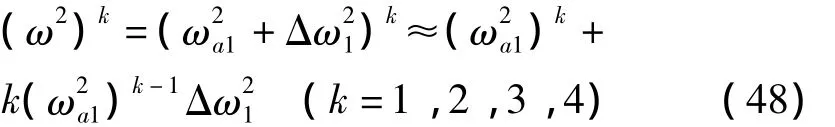
其中:

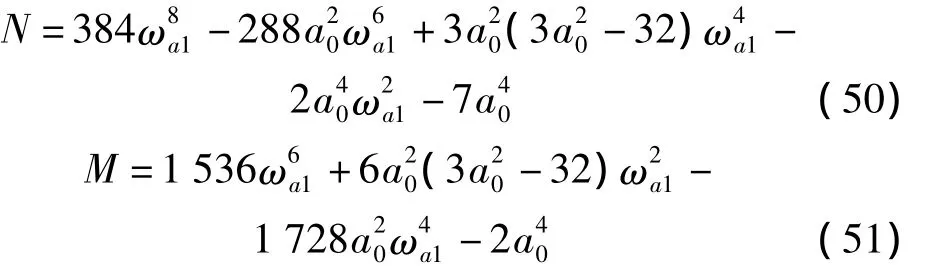
二阶近似角频率ωa2为:

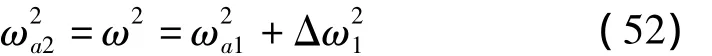
或:

由式(49)～(53)给出的二阶近似角频率与Hu[5]用摄动法得到的二阶近似角频率是一致的。其相应的二阶周期为:

3 讨论

为了说明文中给出的近似解的有效性。用TW2表示Wu等[3]由改进谐波平衡法得到的二阶近似周期，TM2表示Ma等[4]由同伦摄动法得到的二阶近似周期，TH2表示Hu等[6]由迭代法得到二阶近似周期。表1给出各近似周期与方程(14)的精确周期Te在不同初始值a0的比较。表2给出在不同的初始值a0时各近似周期误差的比较。从表1和表2可以看出当初始值a0=1时，一阶近似周期和各二阶近似周期与方程(12)的精确周期相等。当初始值a0＜1时，Ta2和TH2比TW2和TM2要精确得多。近似周期Ta2和TH2比精确周期大，而近似周期TW2和TM2均比精确周期小;当初始值a0＞1时，所有近似周期均比精确周期小。文中给出二阶近似周期Ta2的精度不如TW2，TW2和TH2的精度，但二阶近似周期最差的精度仅为－0.235%。从表1和表2可以看出改进的两变量展开法能够有效地处理这类不含速度线性项非线性Jerk方程。

图1～图3分别给出了一阶近似周期解xa1和二阶近似周期解xa2在初始值a0等于0.1，2和20时与数值解xnum的位移时间曲线图的比较，其数值解xnum是通过用Runge-Kutta法求解Jerk方程(14)得到。从图1～图3可以看出在不同初始值a0，二阶近似周期解与数值解都吻合得很好，二阶近似周期解的精度比一阶近似周期解的精度高很多。当初始值a0较小时，一阶近似周期解的误差比较大，随着初始值a0的增大，一阶近似周期解的与数值解的绝对误差先减小后增大。但是一阶近似周期解在初始值a0＞1时比初始值 a0＜1时的精度要高。

表1 各近似周期与精确周期的比较Tab.1 Comparison the approximate periods with the exact periods

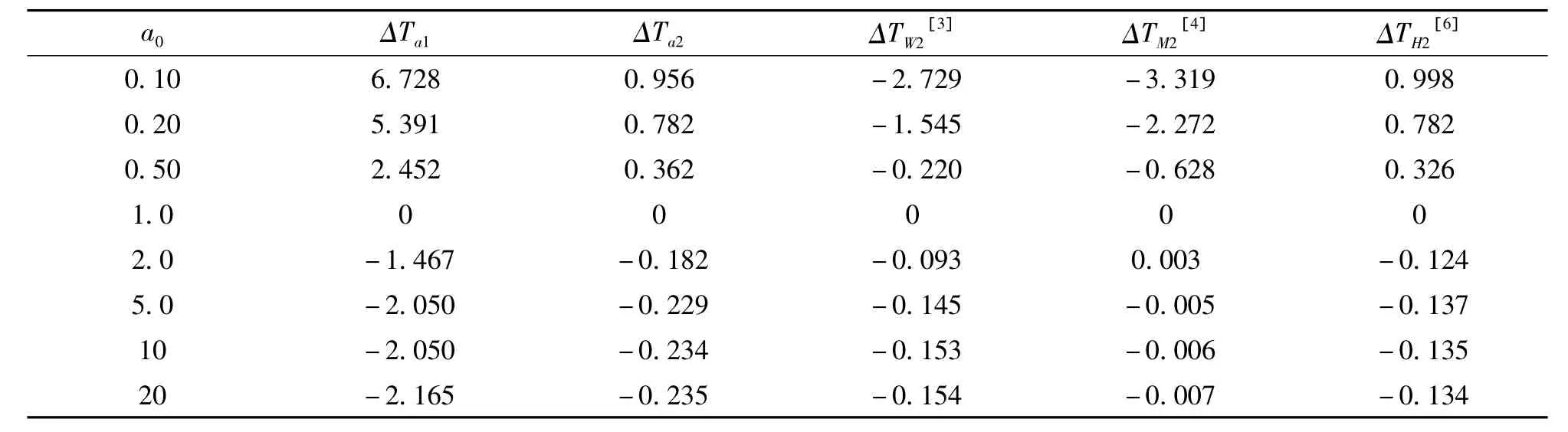
表2 各近似周期误差的比较Tab.2 Comparison the relative percentage error of approximate periods

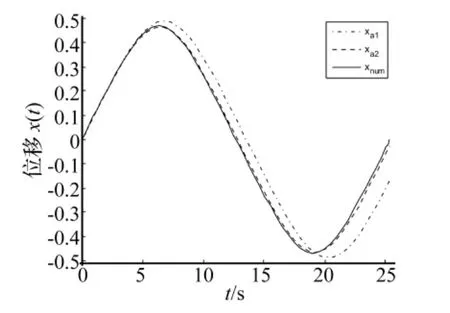
图1 当 a0=0.1，Te=25.359 725时，各阶近似周期解与数值解的比较Fig.1 Comparison the approximate solutions with the numerically exact solution for a0=0.1，Te=25.359 725

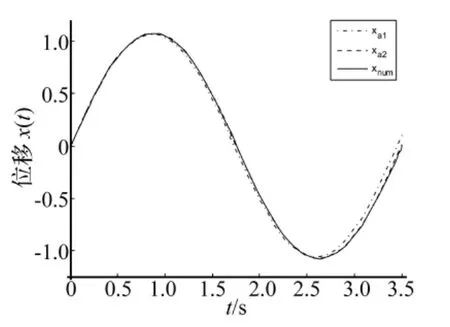
图2 当 a0=2.0，Te=3.508 793 0时，各阶近似周期解与数值解的比较Fig.2 Comparison the approximate solutions with the numerically exact solution for a0=2.0，Te=3.508 793 0

图3 当a0=20，Te=0.370 580时，各阶近似周期解与数值解的比较Fig.3 Comparison the approximate solutions with the numerically exact solutionfor a0=20，Te=0.370 580

文中给出的算例不含速度线性项，如果用经典的多尺度法和经典的两变量展开法求解，则需要在方程(14)两边添加一个线性项ω20x·(ω0≠0)。但这样做使求解得到的近似周期解和近似角频率都与ω0有关，ω0的选取直接影响近似解的精度，当ω0选择不合适时，近似解的误差将非常大。因此经典的多尺度法和经典的两变量展开法不再适用于求解不含速度线性项的非线性Jerk方程。然而改进的两变量展开法结合了Lindstedt-Poincare展开技术，利用式(10)将线性项系数γ表示成系统的频率ω和待定参数ωi的幂级数形式，即使γ=0式(10)也成立。利用改进的两变量展开法求解方程(14)得到的近似周期解和近似周期与线性项系数γ无关，因此改进的两变量展开法能够用于求解非线性Jerk方程，甚至在γ=0的情况下该方法仍然有效。

4 结论

本文应用改进的两变量展开法求解非线性Jerk方程的近似解。与经典多尺度法不同是该方法结合Lindstedt-Poincare展开技术，因此在求解非线性Jerk方程时，即使Jerk方程不含速度线性项改进的两变量展开法对Jerk方程求解仍然有效。文中给出了一个不含速度线性项的非线性Jerk方程的例子，其高阶近似频率是利用牛顿法求解频率非线性代数方程得到。从图表可以看出由改进的两变量展开法得到的二阶近似解的精度很高。结果表明，改进的两变量展开法对非线性Jerk方程求解非常有效，该方法还可以应用于求解其它类似的三阶微分方程。

[1]Mitropolskii Y A，Dao N V.Applied asymptotic method in nonlinear oscillations[M].Kluwer Academic Publishers，Dordrecht，1997.

[2]Gottlieb H P W.Harmonic balance approach to periodic solutions of non-linear Jerk equations[J].Journal of Sound and Vibration，2004，271:671 －683.

[3]Wu B S，Lim C W，Sun W P.Improved harmonic balance approach to periodic solutions of nonlinear Jerk equation[J].Physics Letters A ，2006，354:95 －100.

[4]Ma X Y，Wei L P，Guo Z J.He's homotopy perturbation method to periodic solutions of nonlinear Jerk equation[J].Journal of Sound and Vibration，2008，314:217 －227.

[5]Hu H.Perturbation method for periodic solution of nonlinear Jerk equations[J].Physics Letters A，2008，372:4205－4209.

[6]Hu H，Zheng M Y，Guo Y J.Iteration calculations of periodic solutions to nonlinear Jerk equations[J].Acta Mechanica，2010，209:269 －274.

[7]Nayfeh A H.Perturbation Methods[M].Wiley，New York，1973.

[8]Sturrock P A.Nonlinear effects in electron plasmas[J].Pro.Roy.Soc，1957，A242:277 －299.

[9]Frieman E A.On a new method in the theory of irreversible processes[J].J.Math.Phys，1963，4:410 －418.

[10]Nayfeh A H.A perturbation method for treating nonlinear oscillation problems[J].J.Math.Phys.1965，44:368 －374.

[11]Sandri G.A new method of expansion in mathematical physics[J].Nuovo Cimento，1965，B36:67 －93.

[12]Thomson W T.Theory of vibration[M].Prentice-hall，Inc.，New Jersey，1972.

[13]Awrejcewicz J，Andrianov I V，Manevitch L I.Asymptotic approaches in nonlinear dynamics[M].Springer，New York，1988.

[14]Pakdemirli M，Karahan M M F，Boyac H.A new perturbation algorithm with better convergence properties:Multiple scales lindstedt poincare method[J]， Mathematical and Computational Applications，2009，14:31－44.

[15]Hu H，Zheng M Y.A note on the two-variable expansion method[J].Acta Mechanica，2011，216:351 －357.