小口径火炮弹炮耦合动态响应有限元时程分析
苏忠亭,徐 达,李晓伟,韩振飞
(1.装甲兵工程学院 兵器工程系,北京 100072;2.北京京航计算通讯研究所,北京 100074)
火炮身管的柔性对射击精度影响很大,弹丸在膛内运动时,膛线赋予弹丸旋转运动,以保证弹丸飞行稳定。弹丸膛内运动时,弹带和前定心部与炮膛内壁的接触碰撞会导致身管激烈振颤,炮口振动引起弹丸跳角,直接影响射击命中率。文献[1]建立了弹丸膛内运动引起炮管振动的方程,没有考虑弹丸与身管的碰撞-接触;文献[2]基于多体接触理论,考虑了弹丸弹带、前定心部与膛壁的碰摩,但其有限元法本质上仍将弹性身管简单转化为刚体接触;文献[3]采用等参六面体缩减积分单元,考虑了弹丸弹带和前定心部与膛壁的碰撞及膛线对弹丸的扭转作用,对弹丸在膛内的运动过程进行了仿真计算,但膛线身管结构复杂,很难建立准确的三维模型;文献[4]研究了弹管间隙和加速移动质量对身管振动的影响,采用悬臂梁的振型作为身管的近似模态,无法得到身管的真实模态。由于小口径火炮身管短、膛壁薄,适合采用有限单元法编程求解。本文利用Dubowsky模型,基于有限单元法,将弹带定为弹塑性体,前定心部视为刚体,身管为柔体,分别研究了弹带凹槽部、凸起部和前定心部对身管的瞬态冲击作用,根据弹带行进过程确定身管各单元在各时间步长内所受的载荷谱,最终建立了弹丸膛内运动引起的身管动态响应模型。
1 身管有限元模型
1.1 坐标系的建立
根据结构动力学可知,身管属于内中空悬臂梁的空间轴对称问题,采用圆柱坐标系比较方便。建立坐标系ozρθ,o为以炮膛轴线与膛线起始部端面的交点,oz轴为未变形的身管轴线,oρ轴为身管径向,以o垂直向上为θ角零点,向右为起始方向,如图1所示。
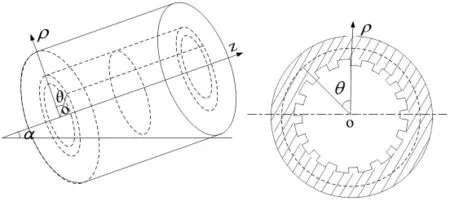
图1 圆柱坐标系下的身管结构Fig.1 Tube structure in cylindrical coordinate system
身管有n条膛线,膛线在oρθ平面内展开曲线为f(z);身管内壁半径为 r1,外壁半径为r2,膛线缠度为η,深度为d,阳线宽为a,弹丸弹带宽为b,前定心部距弹带前端距离为c,射角为α;在t时刻,弹丸质量M在膛内轴向运动速度为v(t),沿膛线旋转速度为ω(t),弹丸膛内运动距离为s(t)=,均由内弹道计算得出。

图2 有限单元划分Fig.2 Division of finite element
1.2 有限单元划分
身管单元包括两部分,阳线部分和其余部分。如图2(a)所示。首先取阳线进行网格划分,轴向以弹带宽b为单元长度的六面体网格,如图2(b)所示。在ozρθ坐标系中,将阳线去掉,对身管进行离散,取轴向长度b,夹角θ,径向dr的六面体网格单元,如图2(c)所示。两种单元通过公用面的节点进行载荷传递。它分为两种情况:阴线内壁的六面体网格单元直接承受弹带凸起部载荷作用;与阳线单元直接连接及不与弹带接触的身管内部结构单元,其节点载荷为由阳线节点传递的载荷或阴线内壁六面体网格单元节点传递的载荷。该六面体网格单元在圆柱坐标系中与三维六面体等参单元的局部坐标系中规则的母单元等效,采用八节点L型插值函数N=[N1N2N3N4N5N6N7N8]作为单元位移函数,单元节点位移向量为={u1,…,u8},其中ui为三个元素的列向量。则单元挠度为:

1.3 单元编码
对于变速弹丸依托膛线旋转前进的身管结构,单元的编码非常重要。结合圆柱坐标系和时间轴,建立四维向量为单元编码。设某单元编码为 ei,j,k,t,其中,i,j,k分别代表整数表示的周向、径向和轴向的递进关系,t为实数,表征在t时刻与弹丸发生触碰的单元。
对于i,由于弹丸弹带的凹槽部和凸起部在内膛圆周对各单元进行触碰,首先对弹带各部编号,i={0,1,2,…,2n-1},以θ角零点为0,顺时针递进。弹丸沿膛线运动时,与弹带各编号对应的阳线和阴线在i上不变;
2 弹炮耦合过程中身管动态响应模型
2.1 弹丸作用下身管的径向动力学方程
将身管简化为膛线起始部一端固定的变截面弹性悬臂梁[5],根据 Euler-Bernoulli梁理论,假设横向剪切应变和横向线应变为零,身管弯曲方程为[6]:

其中:f(z,t)为身管所受的接触力,EI(z)为身管(梁)的抗弯刚度,h为身管速度衰减系数,由身管的结构和材料性能决定。u(z,t)为身管z位置处t时刻的挠度,Me为身管在单元e的质量分布。
初始条件为:
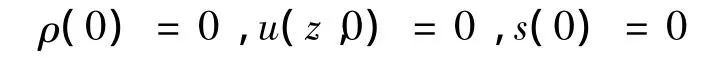
边界条件为:

将弹丸看作移动质量-弹簧-阻尼,弹簧和阻尼分别通过弹带凸起部和前定心部与身管发生触碰。刚度系数和阻尼系数根据接触体的材料弹性模量和几何形状合适选取。如图3所示,弹丸质量M以速度v(t)在膛内运动,通过弹簧K、阻尼C与身管(梁)相互作用,阴线面所受弹丸弹带或前定心部载荷为以身管轴线即悬臂梁中性轴为起点的径向力,大小为:

其中:δ为Dirac delta函数;s(t)为t时刻弹丸膛内运动距离,s(t)=v(t)dt,由内弹道计算得出;ρ(t)为弹丸径向位移为弹簧刚度系数为阻尼系数,塑性变形后的弹带与内膛的接触刚度根据铜-钢的材料弹性模量和几何形状合适选取,前定心部与内膛的接触刚度根据钢-钢的材料弹性模量和几何形状合适选取,阻尼系数采取工程上的经验值。

图3 弹丸移动弹簧-阻尼-质量系统作用下身管悬臂梁模型Fig.3 Tube cantilever beam model under the moving spring,damping& mass system of projectile
弹丸(弹带或前定心部)径向运动方程为:
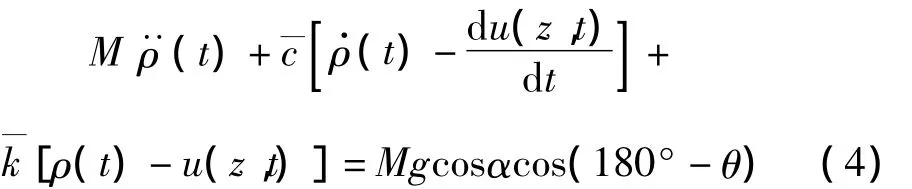
整理得:

由于离散体系的平衡方程是在节点上进行分析的,因此对身管划分的三维单元与平面微分方程之间主要依靠单元的等效节点载荷来衔接,根据静力等效原则,将作用在身管(梁)上的非节点面力载荷转化为等效节点载荷,三维单元的面力等效节点载荷为:
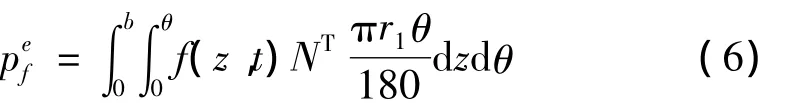
根据弹丸与身管相互作用的不同,将弹丸膛内运动过程分为三个部分:阶段一为弹丸弹带由坡膛挤进膛线过程;阶段二为直膛段弹丸弹带和前定心部与身管共同作用过程;阶段三为直膛段弹丸弹带单独作用过程。如图4所示。
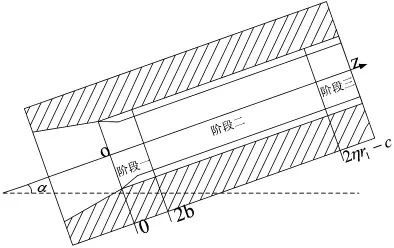
图4 移动弹丸各阶段膛内运动过程Fig.4 Moving process in chamber of projectile
2.2 阶段一身管内壁单元受力分析
在阶段一,弹丸弹带前端面由0到2b。当弹带完全嵌入膛线时,弹带首先为弹性变形,逐步达到屈服极限后过渡到塑性变形,当到达2b点时,弹带塑性变形结束[7]。因本文主要对弹炮系统的径向应力应变进行分析,弹带挤进阶段弹丸对膛线的冲击主要体现在弹性变形阶段[8],在此阶段,可采用弹性变形阶段的弹簧-阻尼-质量系统模拟弹丸与身管的相互作用。
将曲面内壁简化为平面,当弹丸运动到单元e时,联立式(2)、(3)、(6),此单元的外载荷向量为:

式中:Me为单元质量。

式中:Δl为弹带半径强制量。
弹丸没有直接作用的身管单元外载荷为自重:

2.3 阶段二身管内壁单元受力分析
在阶段二,弹丸弹带前端由2b到2ηr1-c。弹带凸起部与阴线膛壁为弹性接触,可采用弹簧-阻尼-质量系统进行模拟,将膛线定义为主面,弹带定义为从面,运用单纯主从搜索算法确定接触点位置;弹带凹槽部与阳线的径向受力为正压力。弹带在轴向受到弹底压力作用、弹前空气阻力作用及弹丸和身管单元的摩擦阻力,而本文的弹炮系统模型描述的是圆柱坐标系下身管径向的受力及运动特征,故不考虑弹底压力和摩擦阻力作用。由于弹管间隙的存在,弹丸前定心部与阳线产生弹性碰撞,之后分离与另一部分阳线产生碰撞,如此反复。
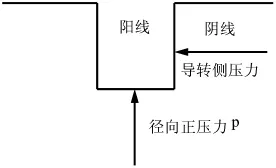
图5 阳线受力分析Fig.5 Force analysis of rifling
阳线受力情况如图5所示,阳线导转侧压力使身管产生左旋回转力矩,对径向变形无影响,故不考虑。因弹带材料采用理想弹塑性线性强化模型,在塑性变形后应力应变仍呈斜率很小的线性关系。为简化计算,取屈服应力σs为弹带凹槽部等效应力。
故径向正压力为:

弹带凸起部与阴线单元e的触碰力模型与式(5)弹带凸起部相同。
弹带凹槽部与单元e的触碰力模型为:

弹丸前定心部与单元e的触碰力模型与式(5)相同,接触分为两部分:初始接触采用单纯主从搜索算法,膛线定义为主面,前定心部定义为从面,搜索初始接触单元;前定心部与膛壁某单元碰撞后弹回,经过两个单侧间隙B、轴向位移和弹丸旋转角度,与下一单元碰撞[9]。设t时刻与弹丸前定心部碰撞的阳线单元为ei',j,k',t,则下一次与弹丸前定心部碰撞的阳线单元为ei'+1,j,k'+1,t,其中,
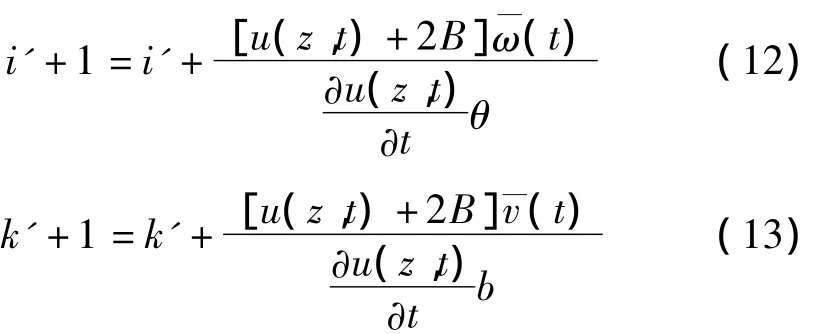
式中:B为前定心部与阳线单侧间隙。
2.4 阶段三受力分析
在阶段三,弹带与身管接触模型与阶段二相同。弹丸前定心部脱离炮口,与阳线不再接触碰撞。故阶段三弹炮耦合数值模型为式(7)与式(9)。
2.5 动力学系统建模及求解
为便于数值求解,综合以上三个阶段,编写MCK矩阵[10],建立系统动力学方程:
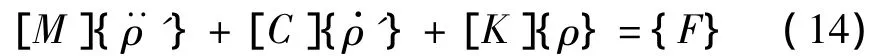
因矩阵[M]、[C]和[K]中有部分是时变的,需要以分块矩阵形式表示,故:

式(15)中,分块矩阵中的上标e即表示了在时间t参与接触的时变单元,附加的刚度、阻尼只与移动荷载直接作用的单元位移有关。
弹丸膛内运动属于移动荷载问题,MATLAB软件内部函数中有专门针对移动荷载问题的ODE求解器[11]。在MCK矩阵基础上,基于四阶五次Ruge-Kutta微分方程进行二次开发,对弹炮耦合系统进行数值求解。
MATLAB提供的ODE45的调用格式为:

其中:odefun为指示微分方程等号右侧的函数句柄,在迭代中计算MCK矩阵中的时变分块。变量tspan为计算范围,变量y0为系统初始状态变量的值。options可以定义函数运行时的参数。T为时间点的列向量,Y为与时间T对应的求解数组。
3 数值计算算例
取 θ=11.25°,M=84.2 kg,m=0.36 kg,r1=0.015 m,r2=0.025 m,d=0.000 3 m,a=0.002 m,b=0.001 5 m,c=0.08 m,η =30,B=0.000 5 m,E=300 GPa[12],h=0.2[12],dr=0.002 m,对于弹带,对于前定心部,根据内弹道计算得到的弹丸膛内运动速度和旋转速度,采用2.5节中数值求解方法,应用MATLAB生成单元信息并进行弹炮耦合动态响应计算,生成的单元个数为105605,节点个数为115 360,其中阳线单元为9 605。取炮口外壁周向θ=0°单元为研究对象,求解其径向(即垂直向)位移。
实弹射击时,选用技术状态良好的武器系统进行炮口振动测试,高低、方位射角均为0°,弹种为曳光穿甲弹,单发射击,在常规靶场进行。在炮口端正上方安装3 000 g加速度传感器,应用NI公司高分辨率数据采集卡4472 B,在PXI-8105平台上采用LabVIEW语言编写测试框图程序,测试与研究对象位置基本对应的单元的垂直向振动位移,总共获得了12组数据。12发弹的地面散布较小,12组振动数据的差异也非常小,由于弹丸出炮口时间较短(约6 ms),该自动炮身管仍处于自由后坐阶段,未压缩缓冲器弹簧,从而与摇架、炮塔、车体等的相互作用并不明显,对测试曲线中前7 s的幅值较低部分取均值并与仿真位移曲线对比如图6所示。
由图6可以看出,两者非常接近,对两者进行相关性分析,corrcoef=0.895,弹炮耦合数学模型较为准确。
分别对炮口内壁周向 θ=0°、θ=90°、θ=180°、θ=270°的单元进行分析,得到弹丸膛内运动时,身管的挠度曲线如图7所示。
由图7可以看出,弹丸绕膛线在膛内运动一周,对内壁各方向触碰规律相似,但由于前定心部的碰撞,各方向又有所差别[13]。改动数学模型,不考虑阶段二中前定心部的碰撞规律,取炮口内壁周向θ=0°为研究对象,得出振动曲线如图8所示。

图6 仿真模型的实测曲线对比验证Fig.6 Comparison of simulated model and tested model
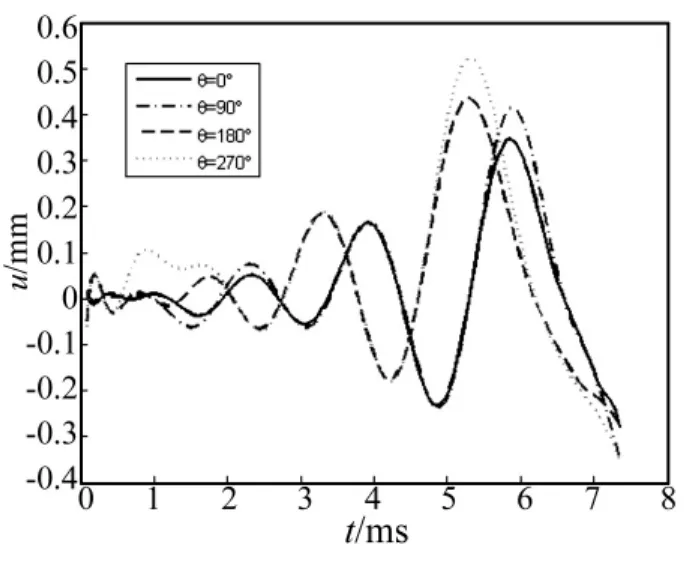
图7 炮口内壁周向各单元挠度曲线Fig.7 Deflection curve of elements inside the muzzle
由图8可以看出,不考虑前定心部的碰撞时,身管振动幅度和频率都较小,可知前定心部的碰撞对弹炮耦合影响很大。
取炮口端面θ=0°处内外壁单元为对象,时间历程内炮口振动曲线如图9所示。

图9 炮口内壁与外壁单元振动曲线对比Fig.9 Comparison of elements vibration inside the muzzle and outside the muzzle
由图9可以看出,与炮口内壁相比,外壁单元的振动频率和幅值都较低,表明与弹丸直接作用的炮口内壁对弹丸影响更大。
4 结论
考虑弹丸弹带挤进过程和刚体前定心部对内膛的瞬态碰撞对身管振动的影响,将弹带凹槽部视为刚塑性体,凸起部应用弹簧-阻尼-质量系统,身管简化为柔性等截面悬臂梁,对从弹带挤进膛线开始到弹带出炮口结束的弹丸膛内运动对身管阳线和阴线单元的触碰作用进行了分析。由于计算量大,比较适合小口径火炮。以某型火炮为例进行了数值计算,在实验验证的基础上对炮口振动进行了分析,得出以下结论:
(1)弹炮耦合过程对炮口横向振动和纵向振动影响规律相当。在一发弹的大约6 ms的膛内运动过程中,炮口各周向单元的径向位移变化规律相同,相对于冲击碰撞,弹丸重力因素影响较小;
(2)弹丸前定心部对炮口振动影响很大,使振动幅值和频率都增大。由于弹丸膛内高速运动的章动性,使弹丸前定心部趋于不碰撞,而本文的数学模型和图8证明了由于入膛时随机碰撞引起的一系列规律碰撞是存在的。
本文建立了适合小口径火炮的较为精确的弹炮耦合数学模型,为建立发射动力学模型和射击精度分析提供了弹炮方面的理论基础,并对其他位置的碰撞分析具有一定的借鉴意义。
[1]周 叮,谢玉树.弹丸膛内运动引起炮管振动的小参数解法[J].振动与冲击,1999,18(1):76 -81.ZHOU Ding,XIE Yu-shu.Solution of barrel vibration caused by motion of bullets in bore by use of small parameter method[J].Journal of Vibration and Shock,1999,18(1):76 -81.
[2]刘 雷,陈运生,杨国来.基于接触模型的弹炮耦合问题研究[J].兵工学报,2006,27(6):985 -987.LIU Lei,CHEN Yun-sheng,YANG Guo-lai.A study on the projectile-barrel coupling based on contact model[J].Acta Armamentarii,2006,27(6):985 -987.
[3]葛建立,杨国来,陈运生,等.基于弹塑性接触/碰撞模型的弹炮耦合问题研究[J].弹道学报,2008,20(3):103-106.GE Jian-li,YANG Guo-lai,CHEN Yun-sheng,et al.A study on projectile-barrel coupling problem based on elastoplastic contact/impact Model[J]. Journal of Ballistics,2008,20(3):103-106.
[4]刘 宁,杨国来.弹管横向碰撞对身管动力响应的影响[J].弹道学报,2010,22(2):67 -70.LIU Ning,YANG Guo-lai.Effect of lateral impact between projectile and barrel on dynamic response of tube[J].Journal of Ballistics,2010,22(2):67 -70.
[5]陈 强,杨国来,王晓锋,等.变速移动弹簧阻尼质量系统作用下梁的动态响应[J].动力学与控制学报,2010,8(3):254-257.CHEN Qiang, YANG Guo-lai, WANG Xiao-feng,et al.Dynamic responses of beam subjected to a moving oscillator with non-uniform velocity[J].Journal of Dynamics and Control,2010,8(3):254 -257.
[6]Nakalswarny K K.Finite element analysis of a projectile during gun launch[D]. BachelorofEngineering in Mechanical Engineering B.I.E.T,Kuvempu University,Karnataka,2002.
[7]孙河洋,马吉胜,张高明,等.弹带挤进过程中膛线的应力分析[J].军械工程学院学报,2008,20(4):43 -46.SUN He-yang, MA Ji-sheng, ZHANG Gao-ming, et al.Analysis of the land stress during the engraving process[J].Journal of Ordnance Engineering College,2008,20(4):43-46.
[8]彭 涛,王学军,黄善文.基于ANSYS的弹带挤进变形及应力分析[J].舰船电子工程,2009,29(11):156 -159.PENG Tao,WANG Xue-jun,HUANG Shan-wen.Analysis on material deformation and stress in the process of driving band engraving based on ANSYS[J].Ship Electronic Engineering,2009,29(11):156 -159.
[9]吴 宏.弹丸膛内外运动及其对射击精度影响研究[D].南京:南京理工大学,2001.
[10]王少钦,夏 禾,郭薇薇,等.变速移动荷载作用下简支梁桥的动力响应及共振分析[J].振动与冲击,2010,29(2):26-28.WANG Shao-qin,XIA He,GUO Wei-wei,et al.Dynamic response and resonance analysis for a simply-supported bridge under speed-varying loads[J].Journal of Vibration and Shock,2010,29(2):26 -28.
[11]Liu K,Reynders E,Roeck G D,et al.Experimental and numerical analysis of a composite bride for hig-speed trains[J].Journal of Sound and Vibration,2009,320:201 - 220.
[12]史跃东,王德石.考虑惯性效应的移动弹丸作用下身管振动特性[J].兵工学报,2011,32(1):414 -419.SHIYue-dong, WANG De-shi. Study on vibration characteristicsofbarrelsubjected to moving projectile considering inertia effect[J].Acta Armamentarii,2011,32(1):414-419.
[13]黄建亮,陈树辉.纵向与横向振动耦合作用下轴向运动梁的非线性振动研究[J].振动与冲击,2011,30(8):24-27.HUANG Jian-liang,CHEN Shu-hui. Study on nonlinear vibration of an axially moving beam with coupled transverse and longitudinal motions[J].Journal of Vibration and Shock,2011,30(8):24 -27.

