基于爆炸声传播时间的声速剖面反演

张 维，杨士莪，黄益旺，唐俊峰，宋 扬

(哈尔滨工程大学 水声技术重点实验室，哈尔滨 150001)

声速剖面反演是海洋声层析技术(Acoustic Tomography)的一种，其实质是根据观测信号的某些特征信息(声线传播时间、简正波相位等)来反推声速剖面的问题[1]。声速剖面反演首先由Munk等[2]提出，他们在深海环境下利用声线的相对时延进行反演，后来，简正波相位反演[3]、峰值匹配[4]以及匹配场方法[5]等多种反演方法逐渐发展起来。近年来，我国学者在利用二维特征声线的传播时间反演声速剖面上做了大量工作[6－7]，即假定特征声线在同一垂直剖面内传播，这在平坦海底或者海底坡度非常小的情况下是可行的。然而，在大陆架海域，由于海底坡度较大，声线在海底反射时将在水平方向上产生明显的偏转，使得声线在三维空间传播。此时，若仍用二维射线声学的方法反演声速剖面将给特征声线传播时间的计算带来不必要的误差，从而降低反演精度。针对此问题，本文利用南海海洋环境反演实验数据，在三维空间搜索特征声线，分析了声线的水平偏转对传播时间的影响，并基于最快特征声线的传播时间进行了声速剖面反演。采用该方法进行声速剖面反演具有以下优势:① 相比于其他特征量，例如声压幅度、相位、多途时延等，最快特征声线的传播时间易于获得;② 声传播时间不受海底声速、密度等参数的影响，在反演过程中无需知道这些参数的准确值，提高了噪声容限[8];③ 射线方法能进行三维声场的计算，进而反演具有复杂海底的海洋环境下的声速剖面;④ 声传播时间计算速度快、精度高。

声速剖面反演是一个多维优化的问题，研究表明，用少量的几阶经验正交函数表示声速剖面是一种有效的方法[9]。本文通过采用全局优化效果较好且计算速度较快的量子粒子群算法[10]搜索经验正交函数系数的全局最优解来反演声速剖面，对考虑和不考虑声线水平偏转两种情况下的反演结果进行了对比。结果表明，考虑声线的水平偏转能使传播时间的计算误差降低一个数量级，进而有效地提高声速剖面反演的精度。

1 实验描述

实验海域如图1所示。海底深度变化较大，1号浮标附近海深大约为100 m，3号浮标附近海深大于1 000 m。文献[11]指出，在实验海域周围布放多个声发射点和接收点，声信号将从不同角度不同途径携带声速信息经到达接收点，途径越多，所获取的信息量越大，声层析的精度越高。另外，水听器间隔太小从声传播时间上不易分辨，太大则会给吊放和回收带来困难，考虑到以上因素在实验中四个浮标大致成正方形分布，每个浮标连接一个长约50 m带有5个水听器的垂直阵，水听器的深度分别为 10 m，18 m，26 m，34 m，42 m。浮标上端都带有GPS装置以实时记录该浮标的位置，垂直阵下端系有重物使得阵始终保持垂直状态。发射船在浮标间按“W”形航迹运动，每隔一段时间投放声弹或手榴弹。图1中A，B，C，D是投弹点的四个位置，A，B，C三点投放声弹，爆炸深度是100 m，D点投放手榴弹，爆炸深度是8 m。声源爆炸后，各水听器在不同距离不同深度上接收到声信号。定义投弹点和浮标之间的连线与经度增大方向的夹角为方位角，逆时针为正。图1中r和α分别表示声源与浮标之间的水平距离和方位角。

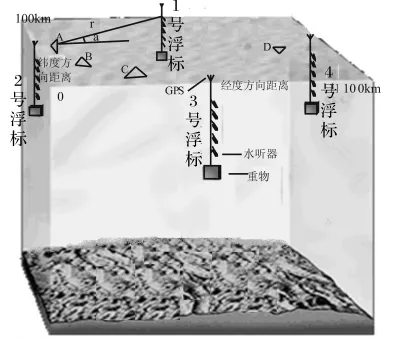
图1 浮标与投弹点位置Fig.1 The position of buoys and bomb-dropping

实验时，声爆炸时刻和爆炸位置都是未知的，只有通过其他的信息估算得到。设GPS每n秒记录一次发射船的位置;投弹前后两次GPS记录的时刻分别为T1和T2，对应的发射船的水平位置分别为(x1，y1)和(x2，y2);声源下沉平均速度为v，爆炸深度为h，发射船监听到爆炸声的时刻为T0;从海面到爆炸深度的平均声速为c0。估算声爆炸时刻T和爆炸的水平位置(x，y)的方法如下:声源下沉时间，该过程中发射船前行距离，爆炸声从爆炸位置传播到监听水听器的时间则声爆炸时刻，爆炸点水平位置

经计算后，声源与浮标之间的水平距离和方位角如表1和表2所示。在实验过程中连续多天采用CTD等设备对该海域不同位置的声速进行了测量，测量结果如图2所示。

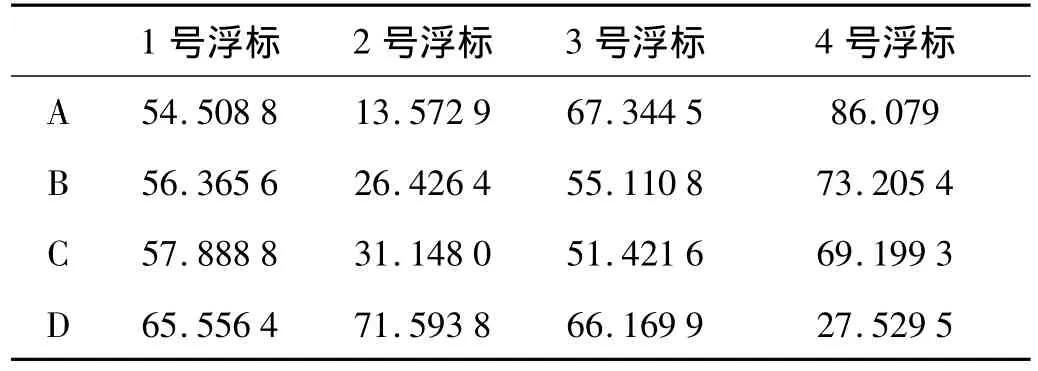
表1 各声源与浮标之间的水平距离(km)Tab.1 The horizontal distance between sources and buoys

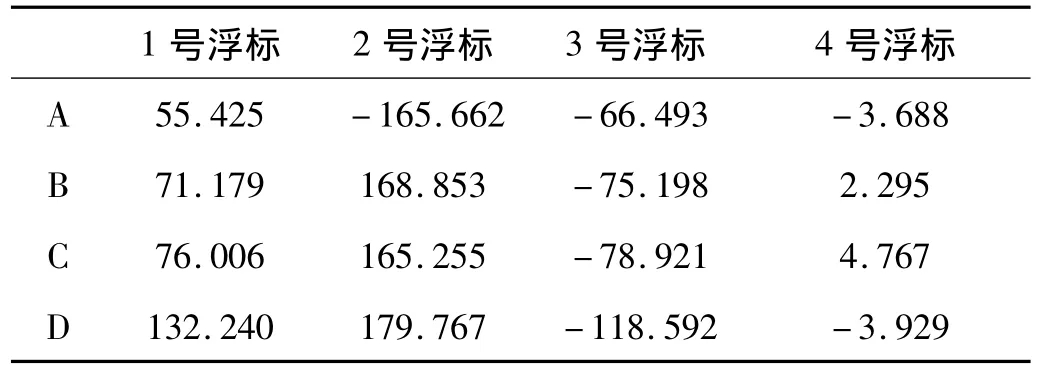
表2 各声源与浮标之间的方位角(°)Tab.2 The azimuthal angle between sources and buoys

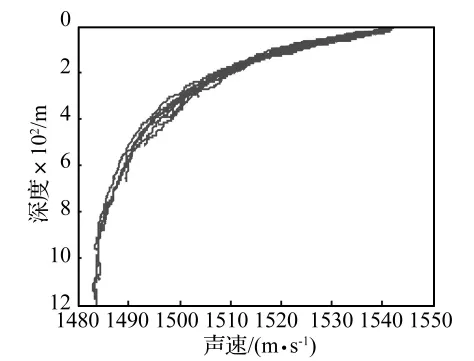
图2 实测声速剖面Fig.2 The measured SSP

2 声传播时间计算模型

作为声速剖面反演的代价函数，声传播时间是影响反演结果精确程度的最大因素，因此有必要建立合理的计算模型进行特征声线的搜索及传播时间的计算。

特征声线搜索的关键点在于出射掠射角的确定，在三维情况下还需要考虑出射方位角的问题[12－13]。为此，本文采用在垂直方向上迭代插值求掠射角，在水平方向上迭代补偿求方位角的办法进行三维特征声线的搜索。

设声源和接收点的位置分别为(x0，y0，z0)和(xr，yr，zr)。由图2可以看到，声速在水平方向上变化很小，因此可以假设声速只是深度z的函数。

声线在传播过程中满足Snell定理和射线方程，分别如式(1)和(2)所示[14]:

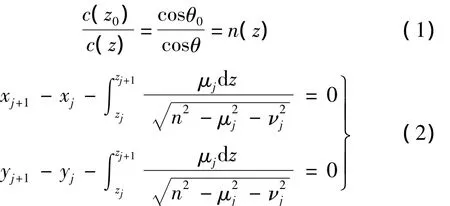
式中:θ和 θ0分别是深度 z和 z0处的掠射角，(xj，yj，zj)和(xj+1，yj+1，zj+1)是第 j段声线的起始点和终止点，uj，vj，sj分别是折射率 n在 x，y和 z方向上的分量。若方位角为 α，则 uj，vj，sj满足:

海底反射时，设海底深度h是x，y的函数，h在x轴和y轴上的一次导数分别是b1和b2，令F=(1+b21)，则海底法向量可以表示为设入射向量为，反射向量为→R =，令 W=s－ bμ － bν，根据入射向j1j2j量、反射向量以及海底法向量之间的关系可以得到:

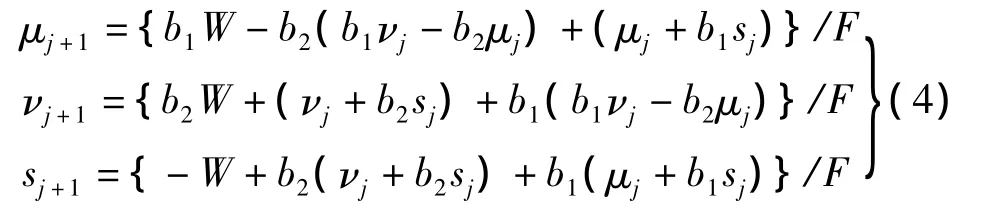
式(4)表征了各反射分量与入射分量之间的关系。当海底梯度不为0，反射向量与入射向量在水平方向上的分量不相等，声线发生水平偏转。

在三维空间搜索特征声线时，首先假设初始出射方位角α为声源与接收点的连线方向，出射掠射角在设定范围内按一定步长分为N等分，按照式(1)～(4)所示的Snell定理，射线方程以及海底反射方程进行单根声线跟踪直到声线终点，然后利用:

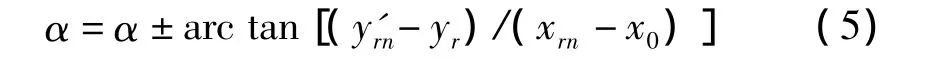
若在二维空间搜索特征声线，可以认为海底反射点处b1≈0，b2≈0，即假设海底深度按照台阶式变化，则 uj+1≈uj，vj+1≈vj，sj+1≈ － sj，从而使得声线只在一个垂直剖面内传播。此时，出射方位角为声源与接收点的连线方向。只需对特征声线的相邻声线进行掠射角线性迭代插值获得特征声线的出射掠射角，即可确定特征声线。

某段声线从深度z1传播到深度 z所需要的时间为:

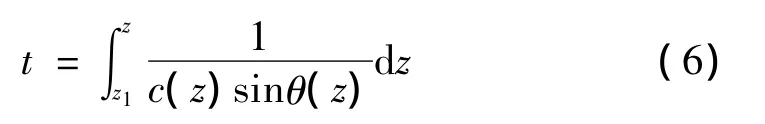
在反转点附近由于sinθ≈0，为了减小数值计算的误差，假定该点附近的声速梯度是恒定的，声速轨迹为一段圆弧，式(6)可以简化为[15]:

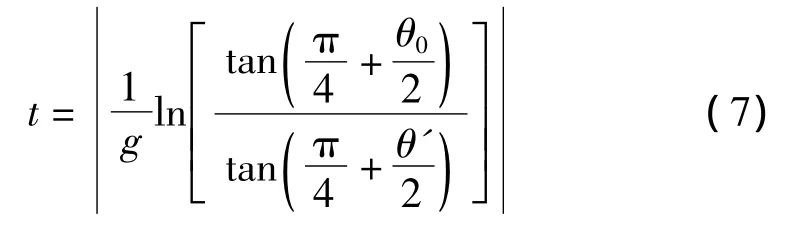
式中:θ0和θ'分别为弧线起始处与结束处声线的掠射角，g是恒定的声速梯度。

3 声传播时间精度分析

声传播时间计算的精确性是有效反演声速剖面的关键，而声线的水平偏转导致二维特征声线和三维特征声线的传播时间不一致，从而使得反演结果存在差异，因此有必要对考虑和不考虑声线水平偏转时声传播时间的精度进行研究。

采用实验现场所测声速剖面，分别在二维空间和三维空间搜索最快特征声线，并计算其传播时间。将声源A，1号浮标作为算例1，声源B，2号浮标作为算例2，声源C，3号浮标作为算例3，声源D，4号浮标作为算例4。算例中均采用34 m深度的水听器。其中，算例2海底较平缓，算例4海底较陡峭，两个算例的最快特征声线传播轨迹如图3所示。

从图3中可以看出，由于声线在海底的反射，二维特征声线与三维特征声线差别较大，尤其是算例4，海底坡度较大，声线的水平偏转较严重。

最快特征声线的传播时间如表3所示。

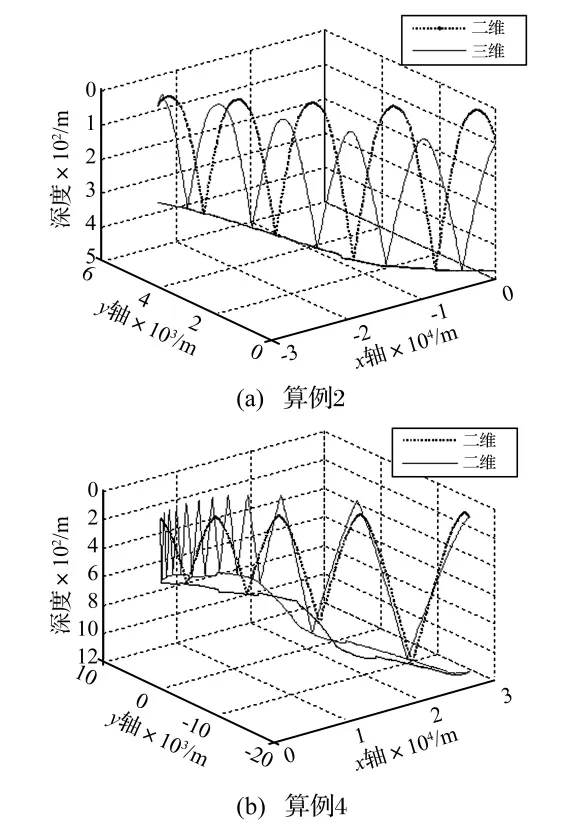
图3 最快特征声线传播轨迹Fig.3 Ray trajectory of rapidest eigenray

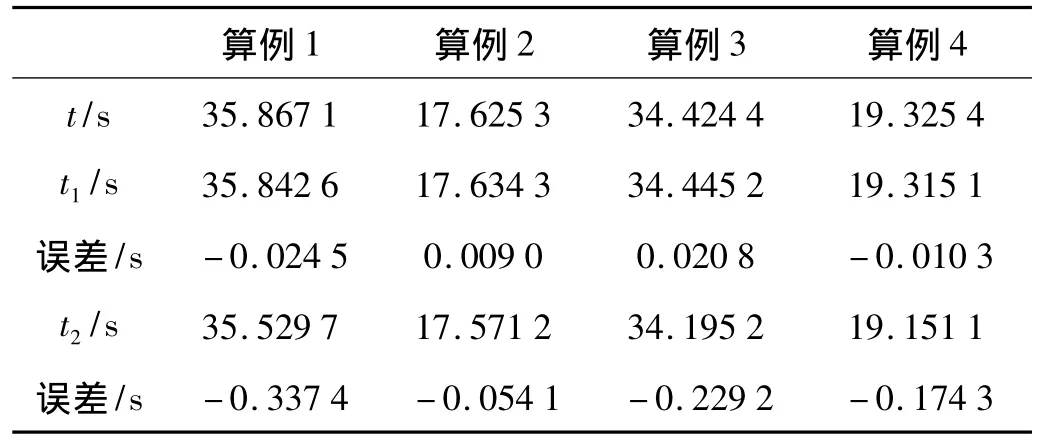
表3 最快特征声线传播时间Tab.3 Transmission time of rapidest eigenray

其中:t是从各水听器接收信号提取的声信号到达时间，t1是在三维空间搜索时最快特征声线的传播时间，t2是在二维空间搜索时最快特征声线的传播时间。从表3可以看出，二维特征声线传播时间的误差明显比三维特征声线传播时间的误差大一个数量级。三维特征声线的误差主要由计算的累积误差产生，一般地，距离越远，这种误差越大。二维特征声线的误差主要由忽略了声线的水平偏转所带来，一般地，海底地形越复杂，坡度越大，这种误差越大。另外，二维空间搜索计算得到的声传播时间在四种算例中均比实测的声传播时间要小。

4 实验数据处理结果

根据17次测量的声速剖面 c1(zi)，c2(zi)，…，c17(zi)和平均声速剖面)求协方差矩阵R，R的每一个元素 rij可以表示为[16]:

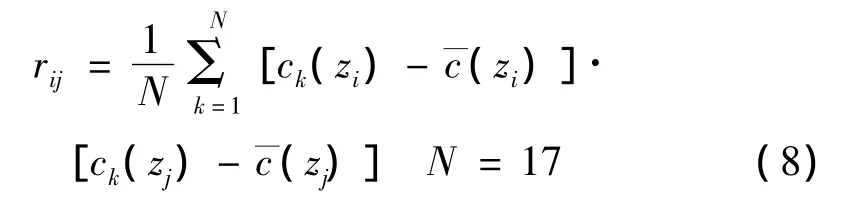
将协方差矩阵进行特征分解，选取前三个最大的特征值所对应的特征向量作为经验正交函数，平均声速剖面和经验正交函数分别如图4和图5所示。

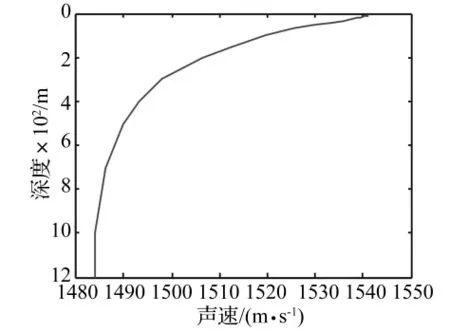
图4 平均声速剖面Fig.4 The average SSP

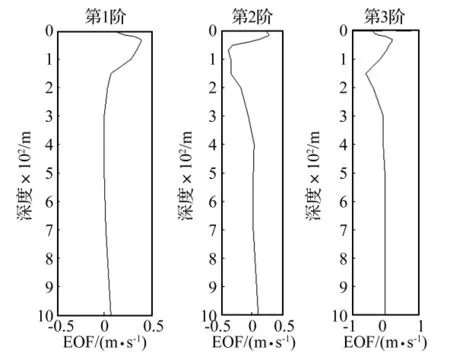
图5 经验正交函数Fig.5 Experiential orthogonal functions

用平均声速剖面和经验正交函数表示待反演声速剖面如式(9)所示[17]:

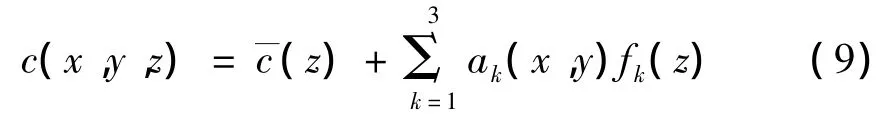
其中:ak(x，y)是待反演参数，由于整个实验过程中声速在水平方向上变化不是很大，因此ak(x，y)可近似认为是常数。

选取代价函数为:

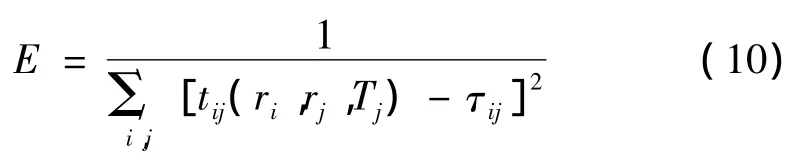
其中:ri，rj分别为声源和接收点的坐标，Tj是爆炸时刻，tij是各水听器收到爆炸声时刻的计算值，τij是实验中各水听器收到爆炸声时刻的观测值。将A、B、C、D四个声源分为A和D，B和D，C和D三组，从各水听器接收信号提取声传播时间，进行三次声速剖面反演。采用量子粒子群作为优化算法，搜索当代价函数最大时ak的全局最优值并代入式(9)获得反演的声速剖面，并定义

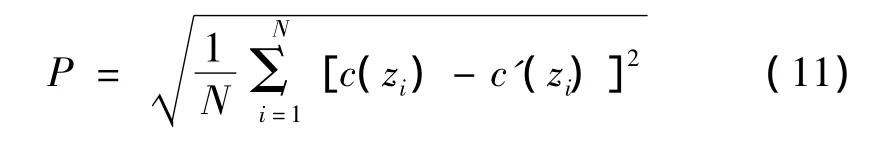
为均方根误差，其中，N为深度点数，c(z)为实测声速剖面，c'(z)为反演声速剖面。

实验现场所测量的声速如图6所示，三组反演得到的声速剖面及误差如图7所示。由于声速变化较大的是在0～200 m深度，200 m以下变化非常小，为更清楚地进行比较，图7中深度只截取0～200 m。图7中用以和反演结果对比的实测声速即为图6中所示的现场实测声速。

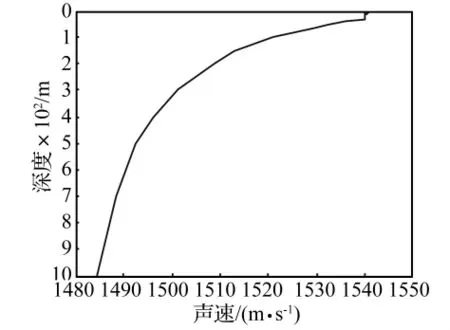
图6 现场实测声速Fig.6 The measured filed SSP

从图7可以看出，三维特征声线声速剖面反演的结果与二维情况下相比误差更小，更接近实测声速剖面。

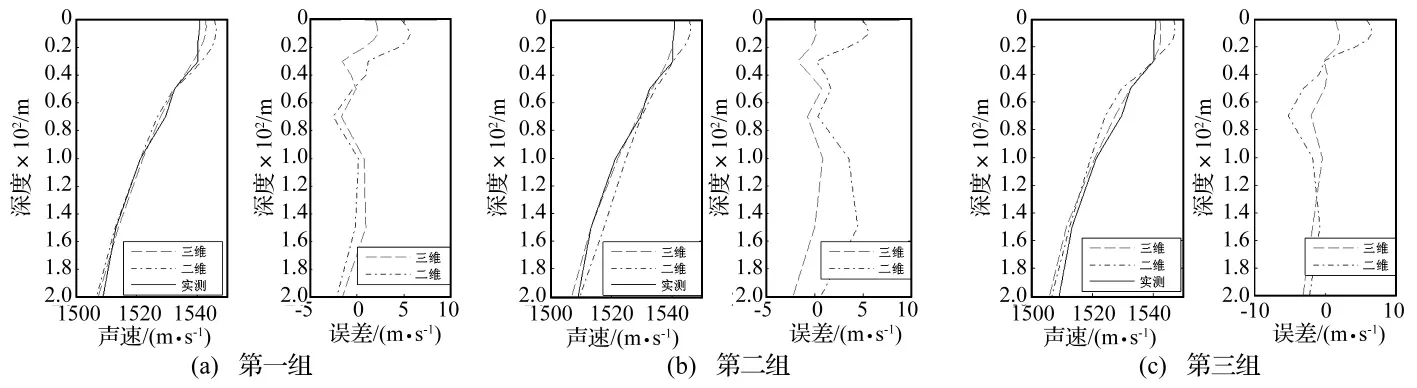
图7 声速剖面反演结果Fig.7 The results of SSP inversion

各组反演的均方根误差和最大误差如表4所示。

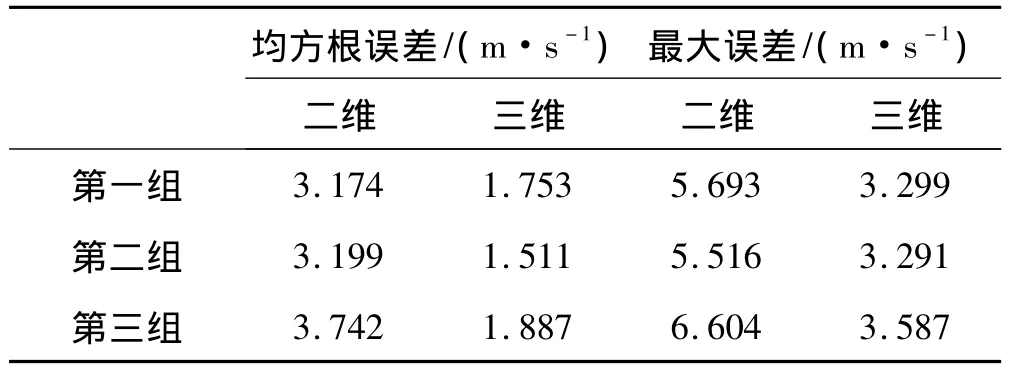
表4 声速剖面反演误差Tab.4 The error of SSP inversion

从表4可以看出，在以上三组反演结果中，第三组反演的误差最大，忽略声线水平偏转时最大误差是6.604 m/s，均方根误差为 3.742 m/s，考虑声线水平偏转时最大误差为3.587 m/s，均方根误差为1.887m/s，也就是说考虑了声线的水平偏转，提高了声传播时间的计算精度，使得声速剖面反演的最大误差和均方根误差都减小了将近一倍。

5 结论

本文首先提出了一种在三维空间搜索特征声线并计算其传播时间的方法。针对实验海域的实际情况计算了最快特征声线的传播时间，并与忽略声线水平偏转情况下的结果进行了对比。通过对比发现考虑声线水平偏转能使得声传播时间计算的精度提高一个数量级。另外，通过对实验数据的处理，以最快特征声线传播时间为代价函数并用量子粒子群算法作为优化算法反演了实验海域的声速剖面。结果表明，考虑声线的水平偏转能使得反演的最大误差和均方根误差都减小将近一倍。由于本文所采用的声速数据在水平方向上的变化很小(见图2)，因此仅反演了声速在深度方向上的变化情况，并不是三维声速反演。在远距离声传播问题中，声速在水平方向上的变化将不容忽略，如何快速有效地反演出声速在三维空间的变化情况将是下一步的工作。

[1]沈远海，马远良，屠庆平，等.浅海声速剖面的反演方法与实验验证[J].西北工业大学学报，2000，18(2):212－215.

[2]Munk W H，Wunsch C.Ocean acoustic tomography A:scheme for large scale monitoring[J].Deep-Sea Res，1979，26:123－161.

[3]Shang E C.Ocean acoustic tomography based on adiabatic mode theory[J].J.Acoust Soc Am，1989，85(4):1531－1537.

[4]Skarsoulis E K，Athanassoulis G A.Ocean acoustic tomography based on peak arrivals[J].J.Acoust Soc Am，1996，100(2):797－813.

[5]Taroudakis M I，Markaki M G.On the use of matched-field processing and hybrid algorithms for vertical slice tomography[J].J.Acoust Soc Am，1997，102(2):885 －895.

[6]唐俊峰，杨士莪.由传播时间反演海水中的声速剖面[J].哈尔滨工程大学学报，2006，27(5):733－737.

[7]张忠兵，马远良，倪晋平，等.基于声线到达时差的声速剖面反演[J].西北工业大学学报，2002，20(1):36 －39.

[8]黄益旺.浅海远距离匹配场声源定位研究[D].哈尔滨:哈尔滨工程大，2005:1－2.

[9]沈远海，马远良，屠庆平，等.浅水声速剖面用经验正交函数(EOF)表示的可行性研究[J].应用声学，1999，18(2):21－25.

[10]杨传将，刘 清，黄 珍.一种量子粒子群算法的改进方法[J].计算技术与自动化，2009，28(1):100 －103.

[11]廖光洪，朱小华，林 巨，等.海洋声层析观测技术与方法[J].海洋学报，2010，32(3):14－21.

[12]王恕铨.求解三维本征声线的一种新方法[J].声学学报，1992，17(2):155－157.

[13]Sethian J A.3－D travel time computation using the fast matching method.[J].Geophysics，1999，64(2):516－523.

[14]Yang S E.Theory of Underwater sound propagation[M].Harbin Engineering University Press，2009.

[15]刘伯胜，雷家煜.水声学原理[M].哈尔滨:哈尔滨工程大学出版社，2006:112.

[16]张之梦，刘伯胜.遗传模拟退火算法用于浅海声速反演的仿真研究[J].哈尔滨工程大学学报，2006，27(4):505－508.

[17]张忠兵，马远良，杨坤德，等.浅海声速剖面的匹配波束反演方法[J].声学学报，2005，30(2):103－107.