直升机雷达天线非定常气动特性数值模拟

冯浩燕

(中航工业直升机设计研究所，江西景德镇 333001)

0 引言

流体试验表明，当雷诺数Re大于临界值时，流动会出现一系列的复杂变化，最终导致流动呈无序的混乱状态。这时，即使是边界条件保持变化，流动也是不稳定的，速度等流动特性都随机变化，这种流场状态称为湍流状态。在绝大多数工程流动问题中，流体往往处于湍流状态，湍流特性在工程应用中占重要的位置，因此，湍流的研究要高度重视。通过对湍流现象的观测发现，湍流带有旋转流动结构，这就是所谓的湍流涡。流体流经物面某位置处，流体的动能可能降为零，同时由于逆压作用，流体回流使得边界层脱离物面，在主流冲击下流向下游，从而形成旋涡涡街。逆压和流体黏性是涡生成的必要条件。图1为冯·卡门实验测得的卡门涡街，很好地描述了这一现象。

图1 卡门涡街

在直升机上安装近似椭圆柱体形状的雷达，根据直升机的飞行速度及雷达特征外形尺寸估算，其工作雷诺数达到106数量级，所以雷达尾流区很可能有成对交替脱落的尾涡生成。交替脱落涡的生成对雷达的工程设计及安装有直接影响。首先，过大的交变载荷为强度设计增加了困难。另外，如果脱落涡频率和天线固有频率发生耦合，则会诱发强力有害的共振现象。同时，过大的交变载荷对全机的稳定性和操纵性也有不利影响。所以，对直升机机载雷达天线非定常气动特性进行数值模拟有很重要的工程应用价值。

1 数学模型和数值方法

1.1 控制方程与湍流模型

根据模型试验状态和全尺寸雷达天线极限工作状态，确定流体介质空气为低马赫数、高雷诺数流体。计算流体为不可压粘性流体。对湍流最根本的模拟方法是在湍流尺度内求解瞬态三维NS方程的全模拟，这无需引入任何模型。然而这是计算机目前的容量及速度尚难以解决的。另一种要求稍低的办法是亚网格尺度模拟，即大涡模拟(LES)。这也是从NS方程出发，其网格尺寸比湍流尺寸大，可以模拟湍流发展过程的一些细节，但计算工作量依然很大。目前工程上常用的模拟方法是由Reynolds时均方程出发的模拟方法，假设湍流中的流场变量由一个时均量和一个脉动量组成，以此观点处理NS方程得出雷诺平均 NS方程(RANS)。再引入Boussinesq假设，湍流计算就归结为湍流粘性系数的计算。我们可以把连续方程和动量方程写成如下的笛卡儿坐标系下的张量形式:

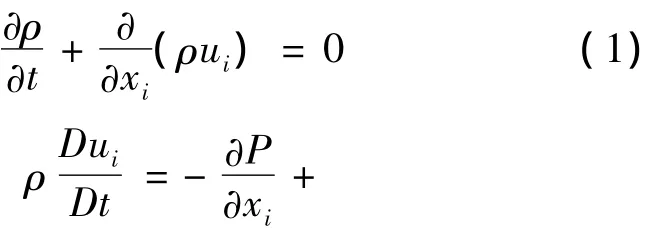
它们和瞬时N-S方程有相同的形式，只是速度或其它求解变量变成了时间平均量。额外多出来雷诺应力，表示湍流的影响。应用Boussinesq假设对方程进行封闭，认为雷诺应力与平均速度梯度成正比，即:

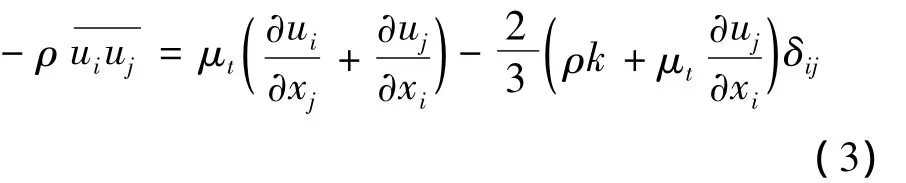
Boussinesq近似的好处是与求解湍流粘性系数有关的计算时间比较少，可将该假设用于κ-ε双方程模型。在κ-ε双方程模型中，只需多求解湍动能k和耗散率ε两个方程，湍流粘性系数由湍动能k和耗散率ε的函数求得认值)。Boussinesq假设的缺点是认为湍流粘性系数是各向同性标量，对一些复杂流动，该条件并不是严格成立，所以具有应用限制性。

计算湍流模型采用Realizable κ-ε模型。Realizable k-ε湍流模型采用了新的湍流粘度公式。方程是涡量扰动量均方根的精确输运方程推导出来的模型，满足对雷诺应力的约束条件，因此可以在雷诺应力上保持与真实湍流的一致。这个特点在计算中的好处是可以更精确地模拟平面和圆形射流的扩散程度，同时在旋转计算、带方向压强梯度的边界层计算和分离流等计算问题中，计算结果更符合真实情况。

1.2 离散方法及格式

控制方程的离散使用有限体积法。有限体积法是通过网格划分将空间区域分解成由离散的控制体组成的集合并在控制体上用积分形式构造离散变量的代数方程，最后将离散方程线化，求解线化方程获得变量迭代解。耦合求解能相对较快地得到收敛解。选用耦合隐式求解方法，离散和耦合的区别就在于它们所使用的线化方法和求解离散方程的方法不同。方程的线化隐式格式是将未知的流体变量(密度、速度、能量等)同已知变量之间的关系用方程组的形式加以表达，然后通过求解方程组获得未知变量值。

离散格式对流项和耗散项都采用二阶迎风格式。时间推进采用二阶隐式格式。隐式非定常计算公式参数包括每个时间步长的最大迭代数和时间步长的大小。虽然从线性稳定性理论分析，全隐式格式是无条件稳定的，但是在非线性系统中，时间步长还是要受到一定限制的。通常在计算开始时，时间步长取得较小，应该把这个时间步定义为流动最小时间常数小一个数量级。而在后续的计算中则可以逐步加大时间步长。根据参考资料数据中的绕圆柱的斯脱拉哈数确定初步计算时间步长为0.001s，然后根据监测的载荷曲线适当调整时间步长Δt=0.0002s。本次计算模型计算的时间步长 Δt=0.0002s，全尺寸的时间步长 =0.001s，迭代稳定后的每个时间步内迭代30次。

2 计算状态

2.1 外形尺寸及计算网格边界

计算网格为结构化网格，为了精确模拟附面层流动，在靠近壁面的区域网格进行了特别加密处理。壁面函数采用标准壁面函数，网格壁面y+达到了湍流计算要求。图2网格总数为1336800，计算域尺寸为14m×14m×20m。全尺寸外形及附面层网格见图3。

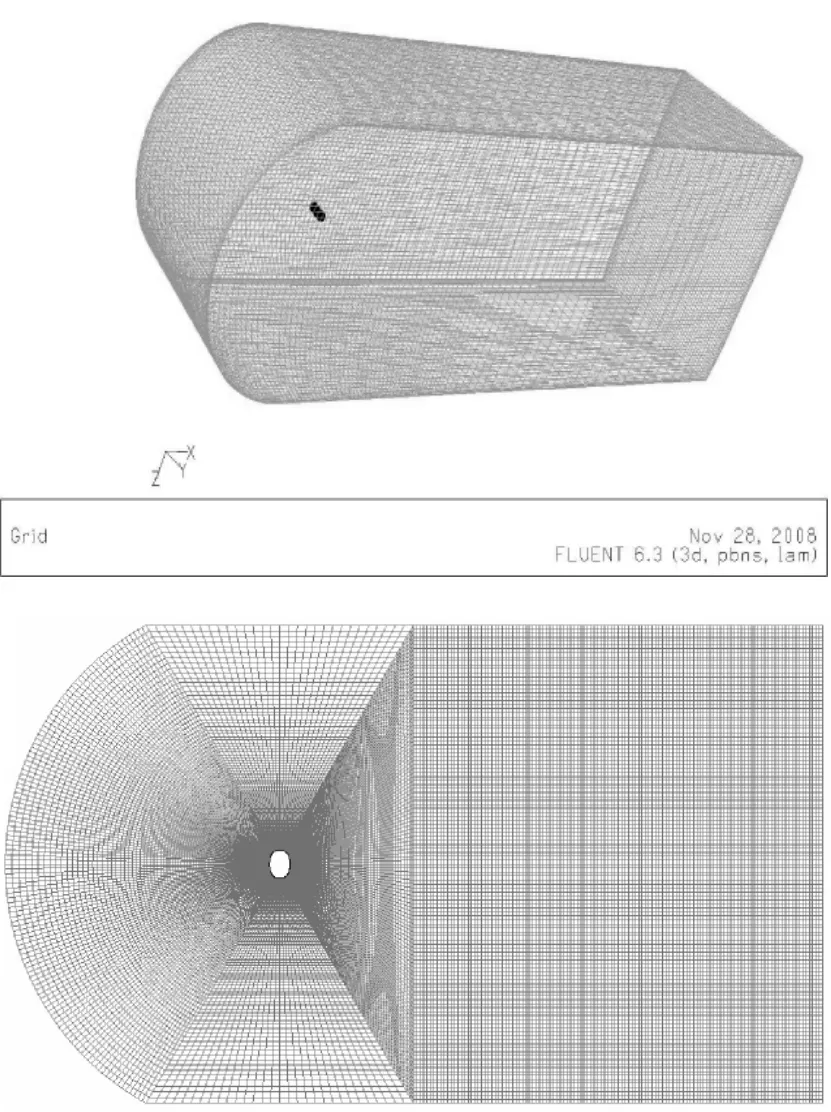
图2 流域网格

2.2 边界条件及计算状态

外场边界条件都定义为压力远场，通过定义压力远场边界的马赫数来模拟雷达承受的风速。雷达表面定义为无滑移物面边界条件。

计算网格为全尺寸雷达和缩比模型雷达两种尺寸，同时为了模拟雷达按装在直升机的工作环境及和前期的试验结果比较，选择计算了三种风速情况，总共六个计算状态。详细参数见表1。

图3 全尺寸外形及附面层网格

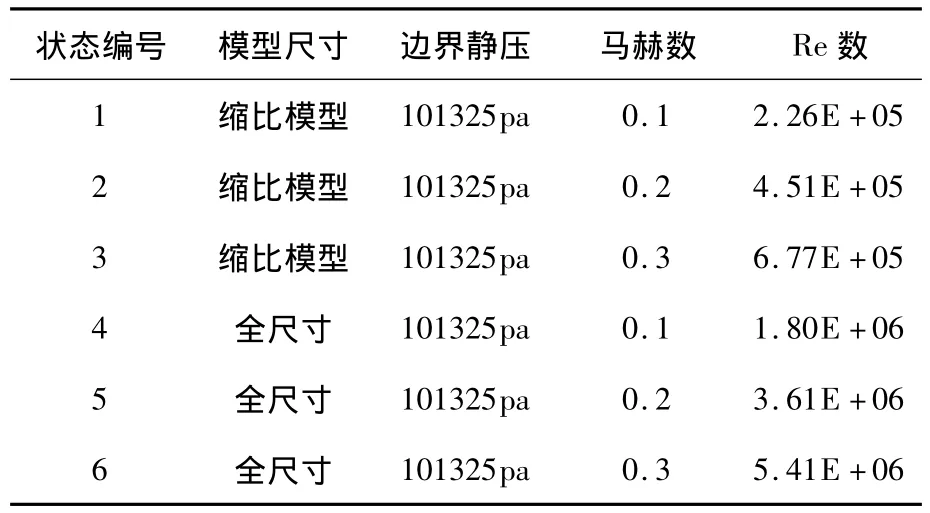
表1 计算状态

3 计算结果及分析

3.1 计算流态分析

计算先进行定常流场计算，收敛后再进行非定常计算，可以更好更快地得到非定常流场解。计算过程对计算残值、升力系数Cl和阻力系数Cd进行了监控记录。发现计算稳定后，载荷成规律性的振荡，如图4和图5所示。各状态流场云图观测到明显的涡生成，如图6和图7所示。载荷周期振荡和流场分布都说明了周期性脱落涡的存在。

图4 Ma=0.1，全尺寸 Cl曲线

各状态的流场分布如图7所示。从图中可以看出脱落涡是成对交替生成，符合环量定律。沿封闭流动流线的环量不随时间而改变，当在旋涡发生体上或下方产生一个旋涡以后，必须在其它地方产生一个相反的环量，以使合环量为0。同时发现随着雷诺数Re的变化，脱落涡的分离点位置和尾流区的大小有所不同，涡道比较规律，有明显的涡街产生。流态是完全的湍流说明计算的雷诺数大于临界雷诺数，但不能精确确定雷达天线的临界雷诺数。

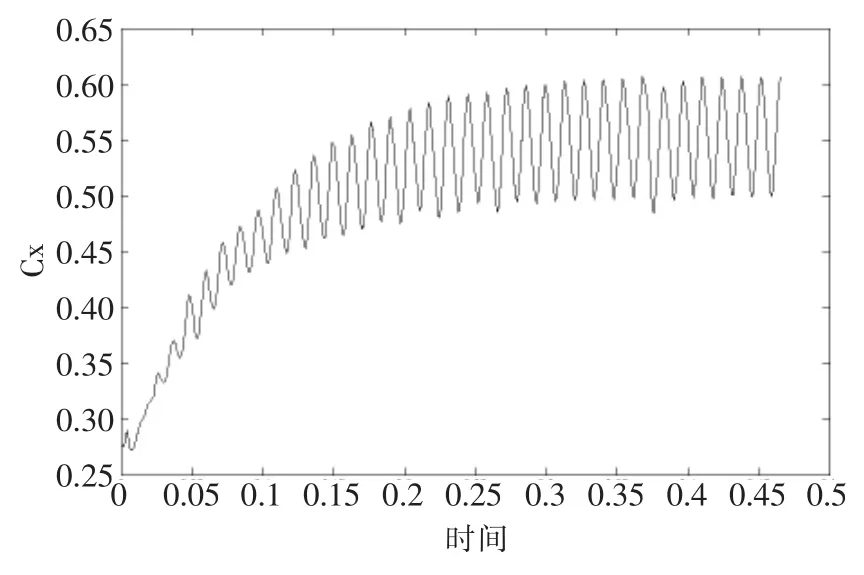
图5 Ma=0.3缩比模型Cd曲线

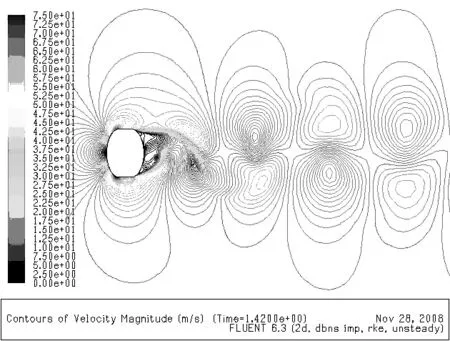
图6 示意流速云图

3.2 计算载荷频率分析

对仿真计算得到的各状态载荷系数时域数据进行傅立叶变换，可以得到雷达载荷的交变频率。分析结果显示阻力系数和升力系数得到相同的频域谱图，这进一步证明载荷振荡为同一激励源，所以可以确定该频率是脱落涡的频率。各状态脱落涡频率见图8。

图7 各状态速度云图

3.3 动特性对比分析

脱落涡的频率及稳定性和斯脱拉哈数St有关。斯脱拉哈数St=f×D/V，f为脱落涡的脱落频率，D为物体的特征尺寸，V为来流速度。表2给出了仿真计算和试验处理得到的各状态的雷达尾部的脱落涡频率和斯脱拉哈数。图9给出了根据雷达模型试验数据分析得出的载荷系数随斯脱拉哈数St变化的情况。分析以上数据发现斯脱拉哈数St随雷诺数Re数量级增大而增大，雷诺数Re在相同数量级的斯脱拉哈数St大小相当。雷达气动特性计算结果和试验结果相当，充分说明该数值计算方法可用于雷达天线的非定常气动特性评估分析。

图8 载荷频域谱

图9 模型雷达试验风速扫描载荷频谱

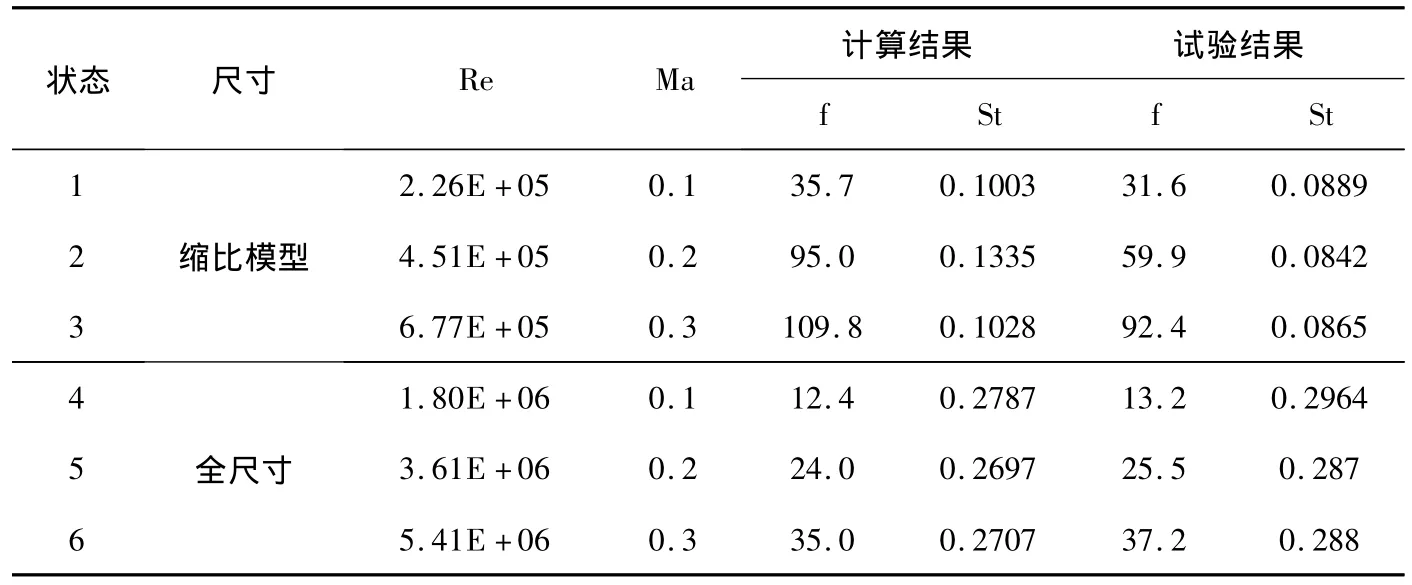
表2 动特性对比

3.4 载荷对比分析

图10比较了全尺寸雷达天线工程估算载荷、仿真计算载荷和试验测试载荷。载荷大小和变化趋势相当，但部分状态计算有偏差，这是由于雷达模型试验保证了雷诺数Re相似，而斯脱拉哈数St相似很难保证，而湍流流态受这两方面条件的影响。另一方面，湍流计算模型的计算精度有限，因为没有一种湍流模型能完全模拟湍流的全部细节。雷达载荷分析有待进一步的试验和计算比较研究。

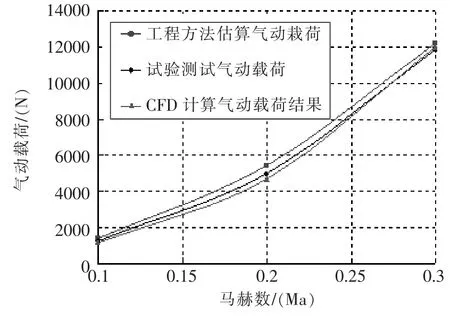
图10 雷达气动载荷比较

4 结论

1)本文采用的数值方法能够很好地模拟雷达天线的绕流流场，描述雷达天线脱落涡的生成和发展，给出非定常气动特性。

2)斯脱拉哈数St随雷诺数Re变化明显，雷诺数Re在105量级时，St=0.11左右;Re在106量级时，St=0.27 左右。

3)计算结果和试验结果比较说明:雷达天线非定常载荷数值模拟结果与试验结果有较好的相关性，能基本反映其非定常气动特性。

［1］王福军.计算流体动力学分析:CFD软件原理与应用［M］.北京:清华大学出版社，2004.

［2］叶春明吴文权.数值模拟圆柱绕流旋涡运动及尾流不稳定性分析［J］.工程热物理学报，1997.

［3］徐元利 徐元春，等.FLUENT软件在圆柱饶流模拟中的应用［J］.水利电机机械，1994.

［4］陈矛章.粘性流体动力学基础［M］.北京:高等教育出版社，1993.

［5］Gverrard J H.The mechanics of the formation region of vortices behind bluff［J］.Fluid Mech，1996(25):401-413.