无轴承旋翼挥舞角与摆振角的测量方法与应用
孟 微,胡和平,周 云
(中国直升机设计研究所直升机旋翼动力学重点实验室,江西景德镇 333001)
0 引言
20世纪60年代开始,为了提高旋翼性能以提升直升机综合性能,陆续出现了无铰旋翼和无轴承旋翼。目前,无轴承旋翼技术已成功应用到BO-108、EC-135、AH-1Z、RAH-66 等直升机上,具有结构简单、零件数量少、重量轻、可靠性高等诸多优点,但其复杂的非线性弹性耦合、运动耦合以及引入的多路传力结构等,使其技术更加复杂化,分析、预测难度大。通过试验方法来进一步加强对复杂的无轴承旋翼弹性运动耦合规律的认识,是突破无轴承旋翼关键技术的有效手段。
无轴承旋翼的挥舞角、摆振角不同于传统的铰接式旋翼的挥舞角、摆振角,它是由柔性梁的弹性弯曲变形产生的,为当量角度。对其挥舞角、摆振角的测量,既是判断柔性梁运动能力的依据,又是获得控制柔性梁应力水平的前提条件。目前,对直升机旋翼旋转状态下弹性变形的测量,国外主要采用以下方法:光栅投影法[1]、立体图像识别法[2-3]、立体图像识别改进法[4]等光学原理测量方法以及传统的应变测量方法[6-9]。
综合分析各方法在试验可行性、试验数据可靠性、方法成熟等多方面的因素,直接测量旋转状态下柔性梁各方向的位移分量,目前在国内现有条件下无法实现;铰接式旋翼上用角位移传感器测量柔性梁各方向运动角的方法[5]在无轴承旋翼结构上无法实现。结合现有的技术条件,针对无轴承旋翼挥舞、摆振由柔性梁弹性弯曲变形产生的特点,本文采用传统的应变电测桨叶弹性变形技术(SPA)与激光位移测量技术相结合的方法,进行无轴承旋翼的挥舞角和摆振角的测量,探索无轴承旋翼弹性运动耦合规律;另一方面,利用CAMRADII软件,模拟试验条件,进行无轴承旋翼挥舞、摆振角度的预测分析,并与试验结果对比与相互印证。

表1 各方法比较
1 无轴承旋翼挥舞角、摆振角的测量方法
本文方法依据测量桨叶弹性变形的应变电测方法(SPA技术)原理,结合激光位移测量而提出。其原理是基于SPA技术的两个假设:
假设1:结构所有位移可表示为前N阶模态位移的线性叠加;
假设2:弹性位移与应变之间具有一一对应的关系。
从而通过弹性变形将旋转状态的位移通过应变与非旋转状态位移建立联系,这种联系要求所测应变为主要反映某独立自由度的影响,即耦合小。对于缩比模型柔性梁,其根部与典型剖面为对称的矩形或十字形结构,挥舞、摆振的全桥布置正好满足这种要求。
无轴承旋翼柔性梁通过弹性变形产生挥舞、摆振运动,其挠曲曲线(外端为直线)可定义当量挥舞、摆振角(如图1)。为此可将挠曲线的位移通过应变与载荷建立关系,推算相应角度。

图1 柔性梁当量挥舞角示意图
为此,对无轴承旋翼挥舞角与摆振角的测量可采取图2的方法,其具体步骤如下:
1)在静态试验中,对柔性梁进行载荷应变标定;
2)用激光传感器测出柔性梁各剖面在不同载荷下的挥舞、摆振位移,拟合出载荷-位移变化曲线;
3)通过位移与角度的几何关系计算出不同载荷下的柔性梁当量挥舞角、摆振角,得到载荷-角度关系;
4)在悬停试验中,结合载荷应变的标定结果,通过应变片、天平等传感器测量旋翼的拉力、扭矩及对应状态下的桨叶、柔性梁等各部件的载荷时间历程,得到其不同旋转状态下的载荷结果;
5)最后,应用静态试验中得到的角度-载荷关系结合悬停试验中得到的载荷结果,计算出不同旋转状态下旋翼的挥舞角、摆振角。

图2 方法示意图
2 测量方法的应用与验证
2.1 载荷、位移、角度关系的建立
2.1.1 测量过程及结果
在柔性梁的静态测量中,用安装在水平台上的分度头固定柔性梁一端,对柔性梁另一端进行加载,应变与位移测量同时进行,测出其不同载荷作用下柔性梁各剖面测点的应变和垂向位移。测试点沿柔性梁轴向布置,如图3、图4所示。

图3 柔性梁挥舞位移测量位置示意图

图4 柔性梁摆振位移测量位置示意图
试验中,分步进行五级加载,挥舞:0kg,2kg,4kg,6kg,8kg,6kg,4kg,2kg,0kg;摆振:0kg,4kg,8kg,12kg,16kg,12kg,8kg,4kg,0kg。每个状态下各测点位移相对变化量采集三次。

图5 挥舞方向加载标定试验示意图

图6 摆振方向加载标定试验示意图
以下是柔性梁静态测试结果。其中,图7、图8为6号柔性梁部分测试结果。图中X轴代表柔性梁轴向位置,Y轴代表位移变化量。位移变化量为实际位移量与零载时位移量的相对值。由图7、图8可知,挥舞方向加载时位移量相对较大,且线性度相对较好。

图7 挥舞方向加载位移结果
2.1.2 关系的建立
根据6、8、9号柔性梁试验结果拟合出不同载荷下剖面位置(x)与位移(y)的关系式,再应用该关系式计算出不同载荷下各剖面位置的位移值,然后根据位移与角度关系计算出各剖面不同载荷下的角度,绘制出110与300剖面下角度随载荷的变化曲线,如图9~图12所示。图中X方向为该剖面所受弯矩,Y方向为角度。由图可知6号与8号柔性梁的重合度比较好,9号略有偏差,剖面位置越大,变形量越大,线性度越好,整体来看试验结果具有较好的一致性。

图9 110剖面挥舞方向加载角度结果

图11 300剖面挥舞方向加载角度结果

图8 摆振方向加载位移结果
表2为根据以上图形绘制出的曲线拟合的8号柔性梁各剖面角度-载荷关系。关系式结果均为线性拟合,且由R2值可以看出该拟合精度较好。

图10 110剖面摆振方向加载角度结果

图12 300剖面摆振方向加载角度结果

表2 角度-载荷关系式及R2值
2.2 悬停状态载荷测量
2.2.1 试验件情况

表3 悬停试验采用的无轴承模型旋翼主要参数
2.2.2 主要试验状态

表4 悬停试验状态
2.2.3 试验结果
图13~图16为6号、8号柔性梁悬停试验的不同状态下(见表4)挥舞、摆振载荷(弯矩N·m)结果,试验数据为等方位采集,64个/圈,共16圈,图中的数据为64个点16圈平均值。图中载荷结果随方位角成周期性变化,剖面位置越接近根部其载荷值越大。
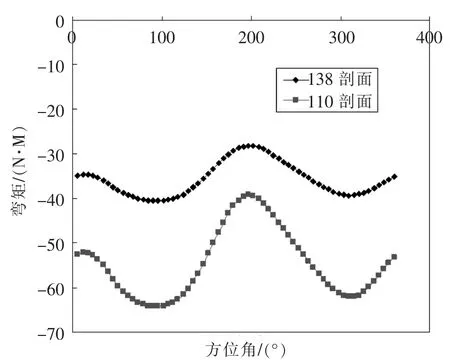
图13 状态1总距6°挥舞载荷

图14 状态1总距6°摆振载荷
2.3 挥舞角、摆振角测量
结合柔性梁静态试验中建立的角度-载荷关系和悬停试验结果,将表3中的关系式对图13~图16等悬停试验载荷结果进行处理,最终得到旋转状态下(试验参数见表4)无轴承旋翼的挥舞角、摆振角,如图17~图26。其中,图17、图18为8号柔性梁挥舞角、摆振角随方位角变化结果。由图可知,挥舞角、摆振角随方位角成周期变化,且周期变距角越大,周期变化越明显。

图15 状态2周期变距-1°挥舞载荷
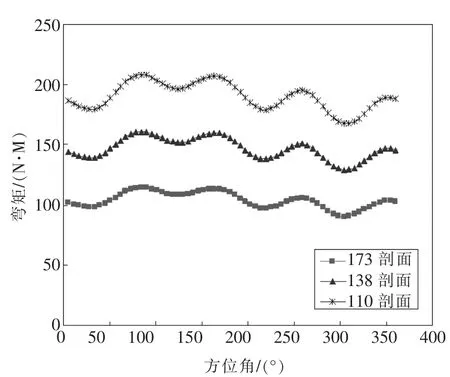
图16 状态2周期变距-1°摆振载荷

图17 110剖面挥舞角沿方位角变化

图18 110剖面摆振角沿方位角变化

图19 挥舞角稳态值随总距变化
图19~图22为8号柔性梁不同剖面挥舞角、摆振角的稳态平均值和1/2峰峰值在状态1下(见表4)随总距变化的结果。由图可知,随着总距的增加,挥舞角、摆振角增加。峰峰值差值随着纵向周期变距的增加而增大。

图20 摆振角稳态值随总距变化

图21 挥舞角1/2峰峰值随总距变化
图23-图26为不同剖面挥舞角、摆振角的稳态平均值和1/2峰峰值在状态2下(见表4)随纵向

图22 摆振角1/2峰峰值随总距变化

图23 挥舞角稳态值随周期变距变化

图24 摆振角稳态值随周期变距变化

图25 挥舞角1/2峰峰值随周期变距变化
2.4 基于CAMRADII计算与试验结果的对比
2.4.1 计算方法简介

图26 摆振角1/2峰峰值随周期变距变化
应用CAMRADⅡ软件进行孤立旋翼配平计算,采用均匀入流、弹性桨叶和弹性柔性梁模型。在试周期变距变化的结果。由图可知,不同剖面的峰峰值差值随着纵向周期变距的增加而增大。验状态下,按拉力为配平目标量,首先计算得到柔性梁测试剖面的位移,再根据沿展向弹性变形位移曲线,得到相关剖面的挥舞、摆振方向的角度。
2.4.2 主要计算结果与对比分析
图27~30为三根柔性梁不同剖面挥舞载荷、摆振载荷在状态1下(见表4)随总距变化的试验结果

图27 138剖面不同总距挥舞载荷

图28 138剖面不同总距摆振载荷

图29 173剖面不同总距摆振载荷

图30 220剖面不同总距摆振载荷

图31 状态1总距6°挥舞载荷分布
图31-图34为不同柔性梁在状态1下(见表4)总距6°和总距9°时沿柔性梁展向分布的挥舞、摆和CAMRADII计算结果的比较。由图可知,计算结果和试验结果在整体趋势上一致性很好,计算结果与试验值基本吻合。振载荷。由图可知,挥舞载荷与计算结果符合度较好,摆振载荷计算结果与试验值一致性也较好。

图32 状态1总距6°摆振载荷分布

图33 总距9°挥舞载荷分布
图35-图38为不同柔性梁在不同状态下随总距变化的挥舞角、摆振角试验值与计算结果比较。由图可知,计算结果与试验结果整体趋势一致,挥舞角在总距0°时略有偏差,摆振计算结果与试验值在小总距时吻合得更好一些,总体来看两者符合程度都可以接受。

图34 总距9°摆振载荷分布

图35 138剖面挥舞角随总距变化

图36 220剖面摆振角随总距变化

图37 138剖面挥舞角随总距变化
3 结论

图38 220剖面摆振角随总距变化
本文提出的无轴承旋翼挥舞角与摆振角测量方法解决了由于无轴承旋翼不能应用角位移传感器进行测量的难题,文中数据分析采用的拟合曲线R2值基本保持在0.99以上,且与计算结果吻合度较好,精度和线性度较高,这表明,本文采用的激光测量位移与传统的应变电测方法(SPA技术)测载荷相结合的方法测量无轴承旋翼的挥舞角与摆振角是可行的,大大降低了试验成本,简化了试验设备,试验结果具有较高的准确度。
该方法的建立,为在悬停和风洞试验中通过对无轴承旋翼弹性变形角度的实时控制,将试验风险控制在一定范围内提供了支撑。
通过该方法,还可以进行各种状态下的无轴承旋翼的挥舞、摆振角的系统测量,为按角度变形进行柔性梁疲劳谱试验提供依据,从而支撑无轴承旋翼技术的深入研究。
[1]Reinert H G,Pengel M K,van der Wall B G.Blade Deflection Measurement at the Low Noise ERATO Rotor[C].26th EUROPEAN RORORCRAFT FORUM,Netherlands,September 2000:104.
[2]Schneider O,van der Wall B G,Pengel K.Final Analysis of HART-II Blade Deflection Measurement[C].29th European Rotorcraft Forum,September 16-18 2003.
[3]Schneider O,Vander Wall B G,Pengel K.HART-II Blade Motion Measured by Stereo Pattern Recognition(SPR)[C].59th Annual Forum of the American Helicopter Society,May 6-8 2003.
[4]Olson L E,Abrego A I,Barrows D A,et al.Blade Deflection Measurements of a Full-Scale UH-60A Rotor System[C].the American Helicopter Society Aeromechanics Specialist’Conference,January 20-22 2010 .
[5]Wang J M.A Successful Comprehensive Rotor Dynamics Correlation for a Sikorsky Full-Scale Bearingless Main Rotor[C].53rd Annual Forum of AHS ,pp1336-1349 April 1997.
[6]Gaukroger D R,Hassal G J W.Measurement of Vibratory Displacement of a Rotating Blade[J].Vertica,1978,(2):111-120.
[7]Gaukroger D R,Payen D B,Walker A R.Application of Strain Gauge Pattern Analysis[C].6th European Rotorcraft and Powered Lift Forum,Paper 19,16-19 September 1980.
[8]Walker A R.Further Application and Development of Strain Pattern Analysis[C].28th European Rotorcraft and Powered Lift Forum 31,Paper 7,August-3 September 1982.
[9]Tourjansky N,Szechenyi E.The Measurement of Blade Deflections A New Implementation of the Strain Pattern Analysis[C].Associantion Aeronautique et Astronautique de France,1992.
[10]Brahmananda Panda.Dynamic Stability of Hingeless and Bearingless Rotor Blade in Forward Flight[C].University Microfilms International,September 1985.
[11]CHENEY M C.Results of Preliminary Studies of a Bearingless Helicopter Rotor Concept[C].28th Annual National Forum,May 1972.
[12]Warmbrodt W,McCloud Ⅲ J L.A Full-Scale Wind Tunnel Investigation of a Helicopter Bearingless Main Rotor[R].NASA Technical Memorandum 81321,Agust 1981

