基于混沌遗传算法优化神经网络方法的救护直升机效能评估与指标优化研究

杜海舰，徐新喜，徐卸古，王运斗，张晓峰

(1.军事医学科学院卫生装备研究所，天津 300161;2.军事医学科学院，北京 100850)

0 引言

由于军事行动多样化及战时卫勤保障立体化的需求，救护直升机的论证与研制是一项迫在眉睫的任务。作为救护直升机研制的立项论证，救护直升机效能评估及指标的综合论证至关重要，尤其是在确定救护直升机机型的基础上，如何对救护直升机指标进行选优并最终评估其保障能力，目前还没有一个科学有效的评价手段。文献［3］采用集对分析方法对救护直升机的机型选择进行了初步研究，但基本上还是采用了线性加权的思想进行评估，没有考虑到影响因素和输出之间的非线性关系，因此有必要采用其它较科学有效的评价方法进行研究。

目前，装备评估有很多方法，如德尔菲法、层次分析法、模糊综合评判法等，但多数以改进算法为主，系统性较差［1］。本文试图采用混沌遗传算法优化神经网络的方法研究救护直升机的效能，并对救护直升机的指标优化进行初步探讨。首先建立救护直升机效能评估指标体系，然后建立BP神经网络，接着采用遗传算法优化神经网络BP神经网络的权值和阈值，期间对遗传算法的种群初始化采用混沌随机序列构造初始种群，从而提高遗传算法的搜索效率。最后BP神经网络预测用遗传算法得到最优个体对网络初始权值和阈值赋值，网络经训练后预测样本输出。BP算法的优点是寻优具有精确性，但同时存在一些缺点，最主要的是易陷入局部极小、收敛速度慢和引起振荡效应等。由于遗传算法具有很强的宏观搜索能力，且能以较大的概率找到全局最优解，所以用它来完成前期搜索能较好地克服BP算法的缺点［2］。将二者结合起来，形成一种混合训练算法-GA-BP算法，达到优化网络的目的，从而为救护直升机的效能及指标的优化提供一个科学的评估手段，为救护直升机研制提供论证基础。

1 救护直升机效能评估指标体系建立

考虑到救护直升机效能及指标选优是一项复杂的系统工程，为便于科学有效地对救护直升机的效能进行评估，需要对救护直升机的效能指标进行分类整理。在前期的数据处理过程中，采用了主成分分析的方法对影响指标进行筛选，这里，主要从作业能力、机动能力、可靠性、成本四个方面着手研究。图1所示为所建立的评估指标体系［3］:

各指标的具体含义如下:

1)作业能力:体现救护直升机基本功能的能力。这里从运送伤病员的人数和救治能力两个方面来考虑。

2)机动能力:包括巡航速度、续航时间、最大航程、升限、机舱容积、最大载重、舱门面积、起降场地直径等8个方面。

3)可靠性:包括卫生装备连续工作的能力、发生故障时的可维修性、寿命周期和装备管理的便利性。这里主要从平均故障间隔时间来考虑可靠性(MTBF)。

4)采购成本:主要是购机成本。

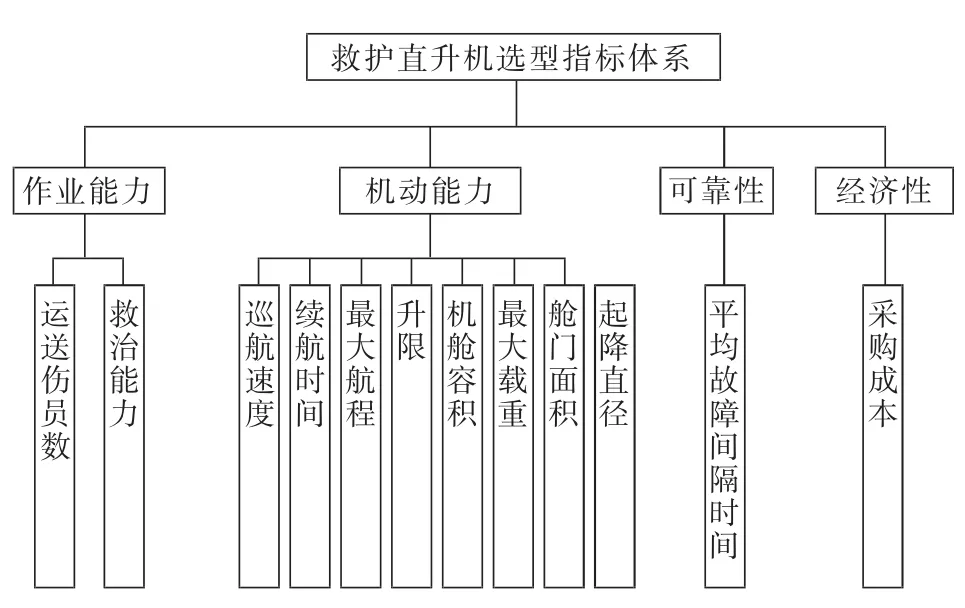
图1 救护直升机效能指标体系

2 评价模型建立

2.1 BP网络结构设计

2.1.1 输入层、隐含层、输出层的设计［4］

对于效能评估，应当依据其关键要素来确定输入层各因素，在神经网络模型中，输入层各因素之间没有相互联系，根据图1建立的评估指标体系可知其输入单元数为12，隐含层节点的确定参考下面单元计算公式:

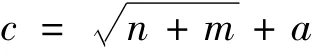
其中c为隐层单元数，n为输入神经元个数，m为输出神经元个数，a为1～10之间的常数。本文中，隐层单元数计算如下:

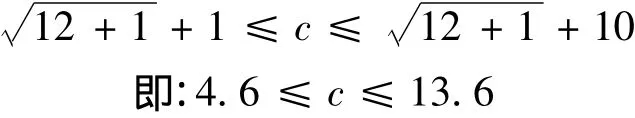
根据c的计算值，由小到大改变节点数训练并检验其精度，当节点数的增加误差不进一步减小时，其临界值即为应采用的值。最后，经过网络的实际训练结果比较，选定网络隐含层节点为9，此时网络能较快地收敛至所要求的精度。2.1.2 目标值及学习步长的选取

效能评估之前，应先根据影响效能评估的因素进行综合预测。在实际操作时，还应结合经验值。若Sigmoid函数选取反对称函数——双曲正切函数，综合评估指标的目标值D的范围也应在［-1，1］之间，也即是综合指标的无量纲数值在［0，1］之间。通常输出单元的局部梯度比输入端的大，所以输出单元的学习的步长应比输入单元小一些。

通过以上分析可得网络模型结构如图2。利用matlab编制了BP人工神经网络模型计算机程序进行训练集样本训练，训练样本数为5，表1为效能评估输入训练样本和检测样本，误差给定为 E=0.0000005，学习步长为 0.1。

图2 效能评估三层神经网络结构图

2.2 遗传算法优化BP神经网络算法的流程

遗传算法(Genetic Algorithm-GA)是一种基于自然选择和基因遗传学原理的优化搜索方法。它将“优胜劣汰，适者生存”的生物进化原理引入到优化参数形成的编码串群体中，按照一定的适配值函数及一系列遗传操作对各个体进行筛选，从而使适配值高的个体被保留下来，组成新的群体，新群体中各个体适应度不断提高，直至满足一定的极限条件。此时，群体中适配值最高的个体即为待优化参数的最优解。正是由于遗传算法独具的工作原理，使它能够在复杂空间进行全局优化搜索，并且具有较强的鲁棒性［2］。

遗传算法优化BP神经网络算法流程如图3所示:

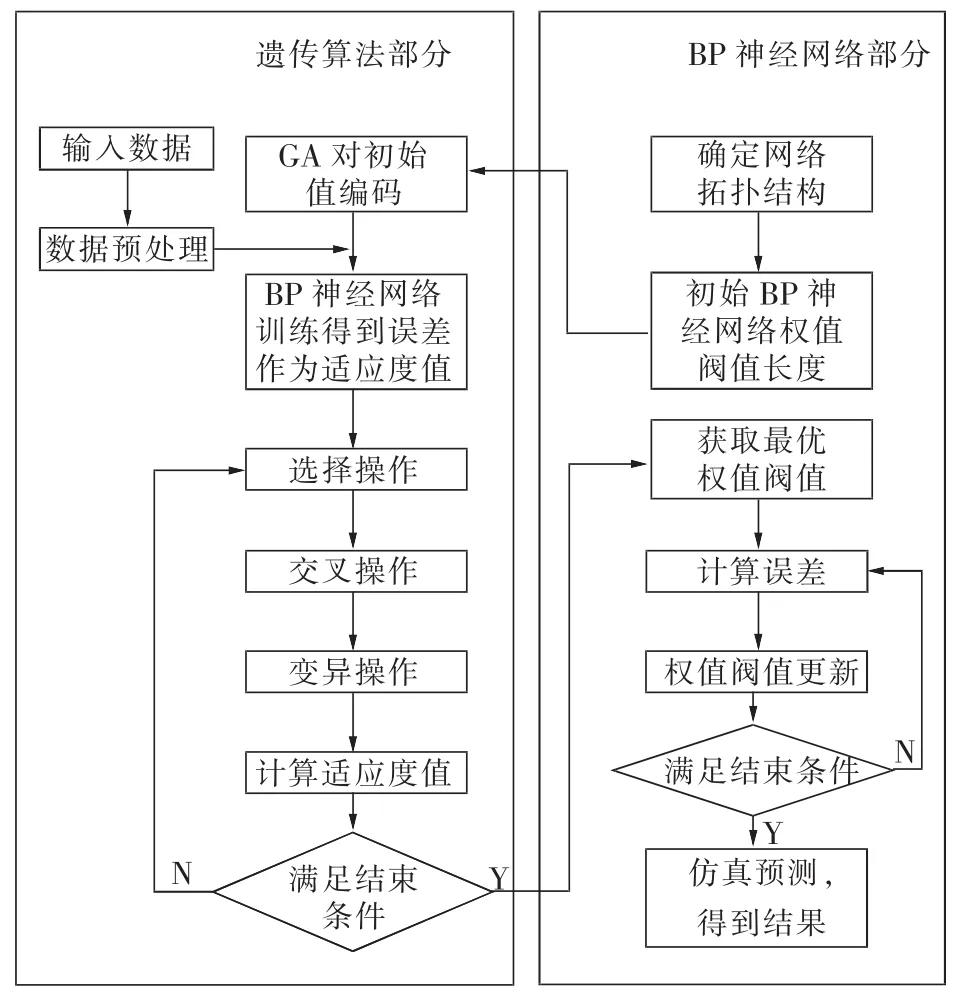
图3 GA-BP算法流程

遗传算法优化BP神经网络分为BP神经网络结构确定、遗传算法优化和BP神经网络预测3个部分。其中，BP神经网络结构确定部分根据输入输出参数个数确定BP神经网络结构，进而确定遗传算法个体的长度。遗传算法优化使用遗传算法优化BP神经网络的权值和阈值，种群中的每个个体都包含了一个网络所有权值和阈值，个体通过适应度函数计算个体适应度值，遗传算法通过选择、交叉和变异操作找到最优适应度值对应个体。BP神经网络预测用遗传算法得到最优个体对网络初始权值和阈值赋值，网络经训练后预测函数输出。

由于救护直升机效能有12个输入参数、1个输出参数，所以设置的BP神经网络结构为12—9—1，即输入层有12个节点，隐含层有9个节点，输出层有1个节点，共有12×9+9×1=117个权值，9+1=10个阈值，所以遗传算法个体编码长度为117+10=127。从机型表中随机找出5种机型作为训练数据，把训练数据预测误差绝对值之和作为个体适应度值，个体适应度值越小，该个体越优。

遗传算法优化BP神经网络的要素包括种群初始化、适应度函数、选择操作、交叉操作和变异操作。由于篇幅限制，这里就不再过多叙述遗传算法的建模过程。需要强调的是:在使用遗传算法初始化种群的过程中，初始种群选取的优劣直接影响遗传算法可行解的分布和算法的收敛速率，而传统遗传算法往往是随机生成初始种群，这种随机性会导致初始可行解的不均匀分布，尤其是当种群规模较小时。因此，为了保证初始种群的多样性和均匀性，使得初始可行解尽可能均匀分散分布在整个解空间［5］，本文利用混沌随机序列构造初始种群，从而提高遗传算法的搜索效率。

3 模型训练与应用

通过收集国内外直升机基本性能数据，主要以我国现有直升机机型做为考察对象，根据图1建立指标数据表。选出救护直升机效能的三级指标12个，除起降场地直径和采购成本2个指标为成本型外，其余10个指标均为效益型指标。为了取消各维数据间数量级差别，避免因为输入输出数据数量级差别较大而造成网络预测误差较大，必须对输入样本进行归一化，如表2所示。

3.1 纯BP算法与GA-BP混合算法模型训练

为了检验神经网络方法的有效性，以表2的前5个样本为训练数据，以后2个样本为检测数据，分别用纯BP算法和GA-BP混合算法分别进行测试。如表3和表4所示为样本训练次数网络误差。

表1 救护直升机效能评估数据表［6，7］

表2 救护直升机效能评估样本(归一化)

表3 纯BP训练样本训练次数网络误差

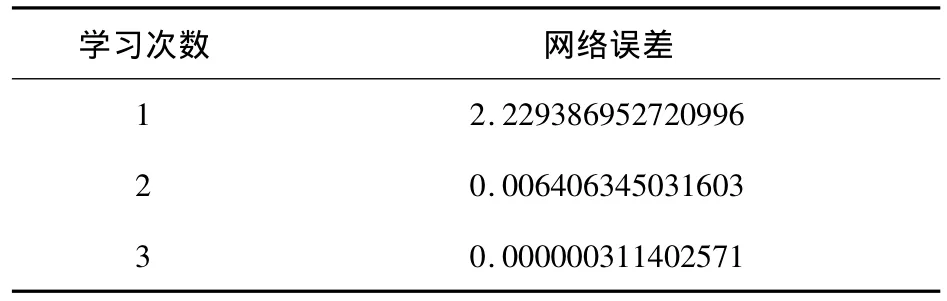
表4 GA-BP训练样本训练次数网络误差

从表3和表4中可以看出，采用GA-BP混合算法只需要3次训练即可满足精度要求，而纯BP算法需要4次训练才能满足精度要求，可见采用GA-BP混合算法要比纯BP算法节省学习次数，效率要高。通常神经网络方法对样本训练时，学习次数一般都需要几百次的训练才能达到精度要求，本例在训练样本时只需2-3次即可满足精度要求，说明救护直升机评估的输出指标与选定的输入指标有良好的趋势性，因此可以更加快速地达到训练要求。图4、图5显示出了两种算法的误差随训练次数的变化过程。

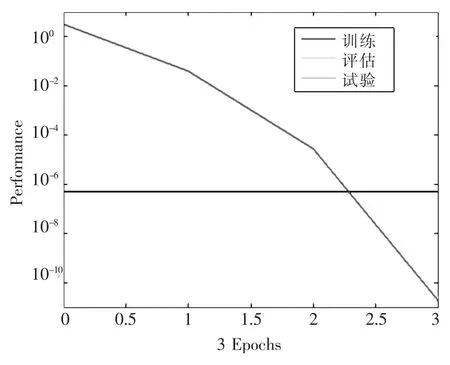
图4 纯BP样本训练学习误差推移图

从测试结果看，采用GA-BP算法除具有较高的效率外，还具有较好的测试精确度，这是由于混合算法先采用遗传算法对神经网络的初始权重及阈值进行了优化，进而提高了测试的准确性。图6、图7所示分别为采用遗传算法进化100代时的适度度和误差平方和随遗传代数的变化图。

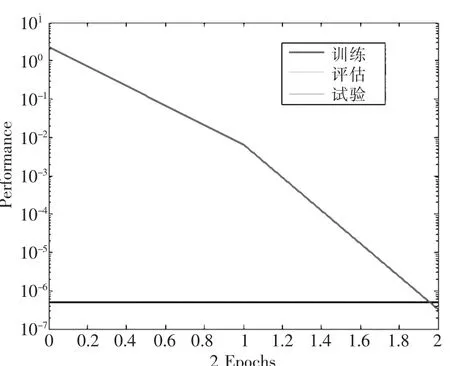
图5 GA-BP样本训练学习误差推移图

图6 GA算法适度度曲线

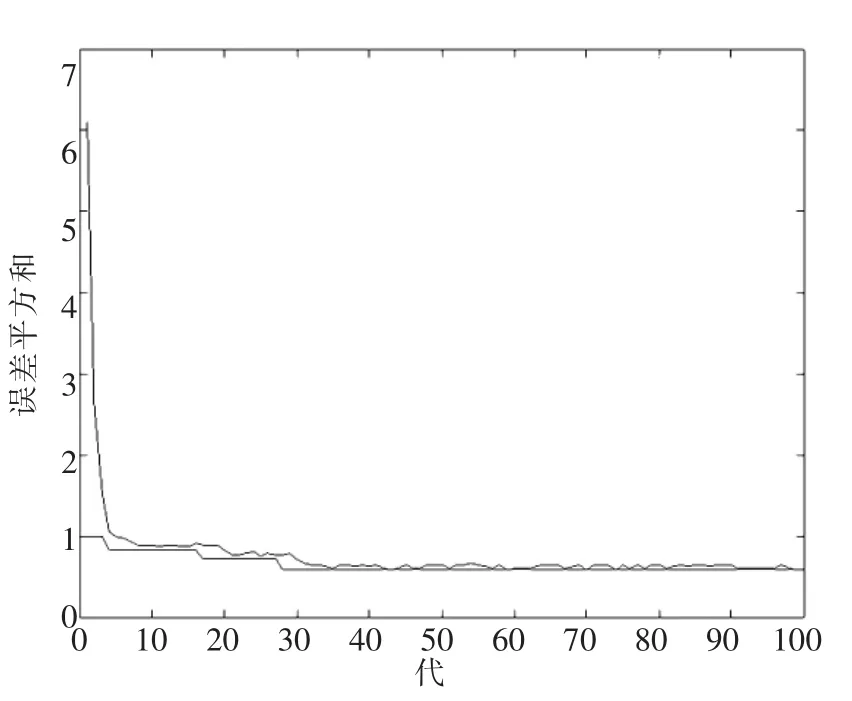
图7 GA算法误差平方和

从图6和图7中可以看出，大约进化到第35代时，适度度曲线及误差平方和基本没有变化，表明种群已经到达优化的目的，可以为神经网络结构提供优化的初始权重及阈值。根据遗传优化结果，可以得出隐含单元到各输入单元的权值和阈值及输出单元到各隐含单元的权值和阈值调整为表5和表6所示。

由于效能评估神经网络模型经训练后，网络精度已经达到要求，可以用检验样本检测预测效果，如表7所示。

表5 隐含单元到各输入单元的权值和阈值

表6 输出单元到各隐含单元的权值和阈值

表7 救护直升机测试样本误差

从表7中可以看出，测试救护直升机评估值时采用GA-BP混合算法的精度要比单纯的BP算法的高。如测试“黑鹰”救护直升机时，GA-BP预测评估值为0.559801，而单纯BP算法的救护直升机评估值为 0.582354，二者的误差分别为 0.007432405和0.029985405，二者的误差数量级为10多倍，说明采用GA-BP算法能够更加精确地评估救护直升机的效能。

从测试结果中同时可以看出，采用GA-BP算法测出的救护直升机评估值最高为0.838912，为米171机型，与实际评估值0.835679非常接近，误差仅为0.003232744，表明采用神经网络的方法能够对救护直升机进行评估并能够准确预测出其效能。

同样，在对救护直升机进行评估时，还可以通过逆向思维反推，对救护直升机的指标进行优化，以期对救护直升机的总体方案提出建设性意见。

3.2 救护直升机指标优化

在已知救护直升机样本数据的基础上，通过本文介绍的遗传算法寻找最优试验条件。思路为:首先根据试验条件数和试验结果数确定BP神经网络结构，然后把试验条件作为输入数据，试验结果作为输出数据训练BP网络，训练后的网络就可以预测一定试验条件下的试验结果。然后把试验条件作为遗传算法中种群个体，把网络预测的试验结果作为个体适应度值，通过遗传算法推导最优试验结果及其对应试验条件［2，8］。其基本思路如图8所示:

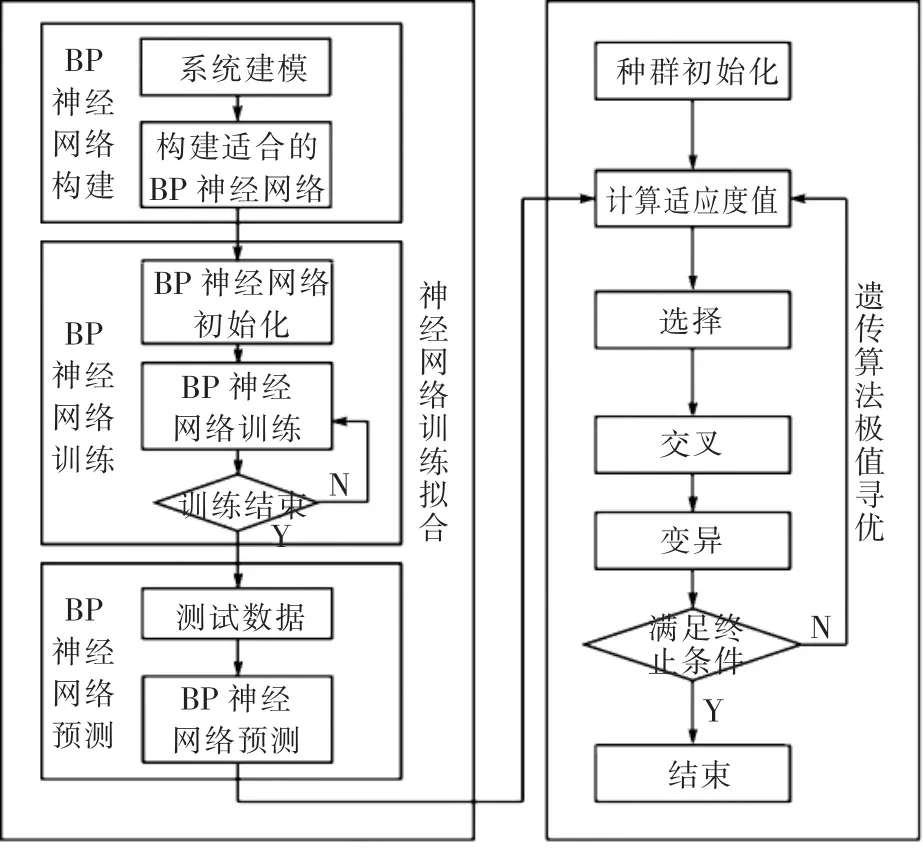
图8 神经网络遗传算法

从表1和表7中可以看出，米171的评估值最大为0.817912，其对应的指标分别为运送伤员12名、救治能力5分、巡航速度250km/h、采购成本7596万元等。在评估数据的基础上，采用神经网络遗传算法寻优，选择的BP网络结构为12—9—1，遗传算法的迭代次数是100次，种群规模是20，交叉概率0.4，变异概率0.2，采用浮点数编码，个体长度为12(即基因由12个指标实数据构成)，最后得到的最优实验结果为0.8473625，对应的实验条件为［10.5 4.6 248.6 3 850.6 5623.5 19.65 4.6 2.65 55 3.8 7600.2］。从优化结果可以看出，运送伤员数10人左右、巡航速度248.6km及最大载重4.6t等为宜，该结果可以救护直升机的指标论证提供参考。

4 小结

本文采用遗传算法与神经网络相结合的方法研究救护直升机的效能评估，建立评估指标与效能评估值的非线性关系，克服了传统线性评估方法的不足，结果表明GA-BP算法能够很好地评估救护直升机效能，并保持了很高的精确度;同时，为进一步对救护直升机的指标进行优化，以期对救护直升机的总体技术方案提供参考意见，本文又用BP-GA算法对救护直升机的指标进行了优化，结果同样表明该方法可以有效地优化救护直升机指标，对今后的救护直升机的工程设计提供指导意见。主要结论为:

1)与传统的AHP方法相比，GA-BP神经网络更能够有效地反应各因素与综合评估之间的非线性关系，更适合评估救护直升机效能。

2)采用纯BP算法及GA-BP算法都能够较精确地评估救护直升机效能，采用GA-BP算法计算救护直升机效能，能够表现出更高的效率及准确性，结果与实际评估值完全吻合。

3)采用BP-GA算法能够对救护直升机的指标进行优化，这是该方法的独到之处，可为救护直升机的总体技术方案提供参考意见，表现出了很强大的应用能力。

［1］张振明.现代 CAPP的应用与发展趋势［J］.CAD/CAM与制造业信息化，2004(1):25-26.

［2］史峰，王小川，郁磊，等.MATLAB神经网络30个案例分析［M］.北京:北京航空航天大学出版社，2010.

［3］杜海舰，王运斗，徐卸谷，等.救护直升机机型选择综合评价［J］.医疗卫生装备，2012(5):32-36.

［4］杜海舰，伍瑞昌.神经网络在未来作战中的床位预测研究［J］.医疗卫生装备，2006，27(5):99-101.

［5］杨蕾，林红.基于混沌免疫遗传算法的神经网络及应用［J］.智能计算机与应用，2011，1(2):10-13.

［6］石海明，杨海平，赵伯诚.直升机医学救护与救援［M］.北京:人民军医出版社，2010.

［7］陈圣斌，周晓光，陈大禄..基于神经网络的直升机可靠性预计［J］.直升机技术，2009(3):31-34.

［8］陈丽娟，余隋怀，初建杰.基于BP神经网络的飞机装备维护人员综合素质评估［J］.航空制造技术，2011(7):93-95.

［9］Kohonen T.Self-Organization and Associative Memory［M］.Berlin Heidelberg:Springer-Verlag，1984.

［10］Farber L A.Nonlinear signal processing using neural networks:prediction and system modeling［R］.Technical Report LA-UR-87-2662，Los Alam os National Laboratory.Los Alamos.NM，1987.