变量代换在求解一阶微分方程中的应用

李丽

（山西大同大学数学与计算机科学学院，山西大同 037009）

变量代换在求解一阶微分方程中的应用

李丽

（山西大同大学数学与计算机科学学院，山西大同 037009）

变量代换是一种重要数学变换，其主要目的是通过代换能使问题化繁为简，化难为易；将不能解决的问题转化为能解决的问题。本文通过实例，探讨了变量代换法在求解一阶微分方程中的应用。

变量代换；一阶微分方程；齐次方程

所谓变量代换法，就是把某个式子看成一个整体，用一个变量代替它，从而使问题得到简化，这也叫换元法。换元的实质是转化，关键是构造元和设元，理论依据是等量代换，目的是变换研究对象，将问题移至新对象的知识背景中去解决。变量代换法是高等数学理论和方法的重要工具之一，在高等数学领域中有着广泛的应用。如在代数中求极限、求导、求积分等，在微分方程中求齐次方程、欧拉方程、微分方程组等[1—5]。本文对变量代换在求解隐式微分方程与微分方程组中的应用作了初步研究。

1 在解齐次方程中的应用

即

将上式分离变量，即有两边积分，得到

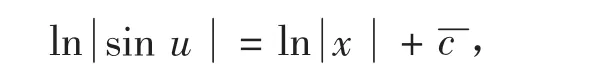
此外，方程（1）还有解

tan u＝0，

即

sin u＝0。

如果在（2）中允许c＝0，则sin u＝0也就包括在（2）中，这就是说，方程（1）的通解为（2）。代回原来的变量，得到原方程的通解

2 在解一阶微分方程中的应用

2.1 在一阶线性方程中的应用

一阶线性方程的形式

其中，p（x），q（x）为已知函数。该方程所对应的齐次方程的通解为

y＝ce-∫p（x）d x，

作代换

y＝c（x）e-∫p（x）d x，

以此作为原方程的解，代入原方程中得

从而解出c（x），进而得出原方程的解。

的通解为y＝cex，可得齐次线性方程的通解

2.2 在一阶隐式微分方程中的应用

一阶隐式微分方程的一般形式为

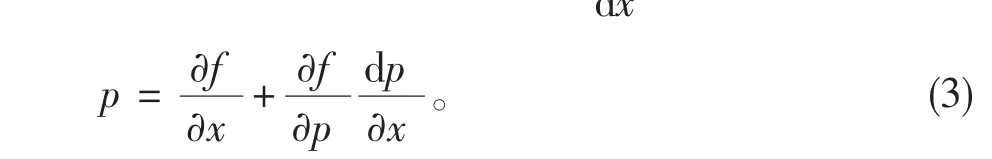
（3）是关于x，p的一阶微分方程，但它的导数已解出，于是可解出方程的解。

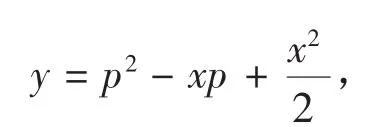
两边对x求导，得到

或

又由2p-x＝0解得

3 结束语

通过以上几类微分方程的分析可以看出，变量代换作为一种基本技巧，是求解一阶微分方程问题的重要方法。它可将复杂的数学形式及不可直接求解的形式通过变量替换进行形式转化，使问题变得简洁，且易于求解。

[1]王高雄，周之铭.常微分方程（第3版）[M].北京：高等教育出版社，2006.

[2]刘显凤.变量代换在高等数学中的应用[J].高校讲坛，2006（15）：164-165.

[3]张东.变量代换法在求解微分方程问题中的应用[J].辽宁交通高等专科学校学报，2003，5（4）：54-55.

[4]许敏伟，吴炳华.变量代换在求解微分方程中的应用[J].徐州教育学院学报，2008，23（3）：171-172.

[5]何彩香，张媛祥.换元思想在解高数题中的应用[J].大理学院学报，2004，3（3）：87-88.

〔责任编辑 高海〕

Variable Substitution in Some App lications of Higher M athematics

LILi
（School ofMathematics and Computer Science，ShanxiDatong University，Datong shanxi，037009）

Variable substitution is an important form of mathematical transformation，the purpose of which is to simplify problems.This paper，with examples，discusses the application of variable substitution in solving firstorder differential equations.

variable substitution；f irstorder differential equations；h omogeneous equation

O175.1

A

1674-0874（2012）04-0006-02

2012-05-25

李丽（1975-），女，山西左云人，助教，研究方向：计算机算法。