厚壁型钢冷弯应力分析
胡盛德,刘 勇,贾余超,黄才志,宋高伟,王 帆,赵文静
(武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室,湖北武汉,430081)
厚壁型钢冷弯应力分析
胡盛德,刘 勇,贾余超,黄才志,宋高伟,王 帆,赵文静
(武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室,湖北武汉,430081)
以厚壁矩形钢管为研究对象,在冷作硬化实验的基础上,对厚壁型钢的塑性弯曲应力沿板厚方向的分布进行解析分析,对其冷弯回弹应力进行数值模拟,将弯曲应力和回弹应力叠加计算冷弯厚壁型钢沿板厚方向的残余应力分布。结果表明,变形外区拉应力由钢板外表面向中性层递减,变化幅度较大;变形内区压应力变化幅度较小;残余应力沿板厚方向近似线性分布;切向残余应力较大,最大值出现在板带的中性层附近。研究结果与相关文献给出的测量结果基本一致。
冷弯厚壁型钢;残余应力;硬化;有限元法
冷弯型钢是制作轻型钢结构的主要材料,广泛应用于建筑、汽车制造、机械制造等各个行业,其品种也朝大规格厚壁方向发展。冷弯型钢残余应力主要由截面成型过程中的塑性变形引起,它影响受压构件的稳定承载力、疲劳强度和抗应力腐蚀开裂能力,目前一般通过实验测量、理论分析和数值模拟方法对冷弯型钢残余应力进行研究,其中测量方法耗时、昂贵,难以获得型钢内部应力分布和建立残余应力与工艺参数的对应关系[1-2]。本文以厚壁型钢冷作硬化实验为基础,对塑性弯曲应力进行解析计算,对冷弯回弹应力进行数值计算,将两种应力叠加以获取型钢截面残余应力分布。
1 冷作硬化效应与材料模型
笔者对某厂矩形钢管的冷作硬化效应进行了系列实验[3],钢管母材为Q345热轧带钢。钢管横断面上弯角、平板处的取样位置和编号见图1,型钢规格和实测尺寸见表1,表中t0为带钢原材料厚度。
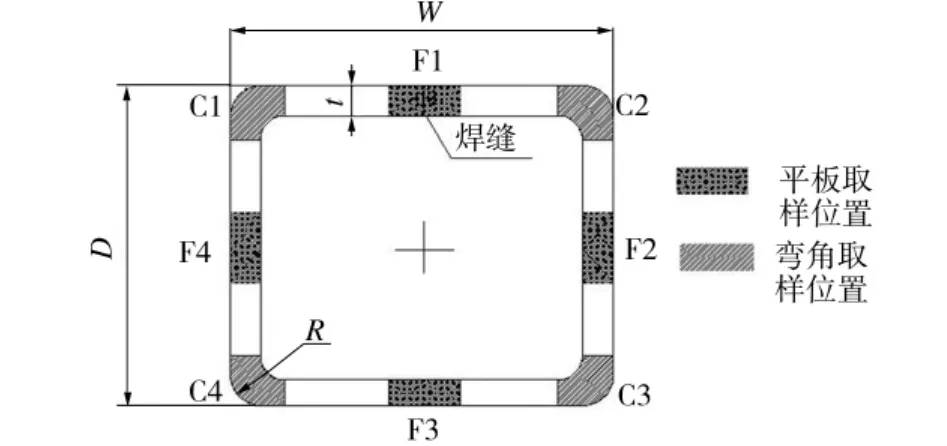
图1 试件取样位置及编号Fig.1 Definition of symbols and sampling location
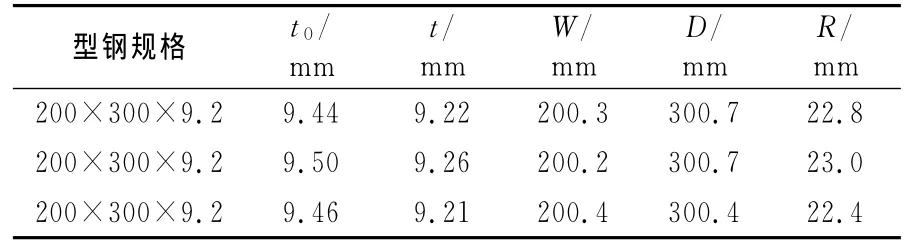
表1 型钢规格及实测尺寸Table 1 Nominal and measured dimensions of the tube
板材试样均采用板状带头长比例形式,如图2所示,其中,l0为试样标距,l0=11.3,F0为标距段横截面积;l为平行段长度,l=l0+2× 20;t为试样厚度;b为试样中部宽度,取为30 mm;B为试样头部宽度,B=b+10;R′为过渡段圆弧半径,取为20~40 mm;h为试样头部长,取为60 mm;h1为圆弧过渡段长度,取为15~20 mm;L为试样总长。在母材上沿带钢宽度方向取样12个,在矩形钢管的平板和弯角处,每个部位取样3个。
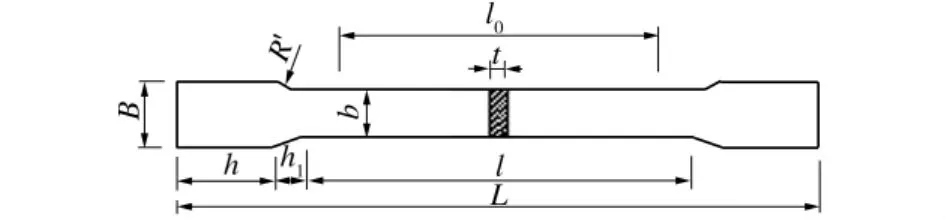
图2 试样设计图Fig.2 Schematic diagram of the sample
经过测试得到,矩形钢管母材边部试样的屈服强度为375.0 MPa、中部试样的屈服强度为363.3 MPa,表2为矩形钢管成品不同取样位置的平板和弯角试样的屈服强度平均值,其中Δ为矩形钢管成品试样的屈服强度相对于母材试样屈服强度的提高比例。
由表2可见,与母材试样的屈服强度相比,不同取样位置的钢管弯角试样屈服强度提高程度比较均匀,平均提高45.1%,而不同取样位置的钢管平板试样屈服强度差别较大,其中,中央带焊缝的平板试样(取样位置为F1)屈服强度提高很明显,提高了44.5%,这主要是由试样中的焊接脱碳层和过热区魏氏体组织导致[3]。
在应力计算与分析中要用到材料的本构关系模型和力学性能指标。对矩形钢管母材Q345热轧带钢试样进行拉伸实验,得到应力-应变曲线,据此回归拟合出材料的双线性硬化模型,当实验数据与双线性模型对应数据点的流动应力差平方和最小时,认为获得了最佳模型。图3为一个母材试样的双线性模型回归拟合结果,应力分析时取几个试样的双线性模型参数的平均值。
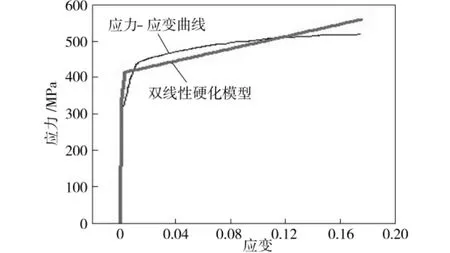
图3 母材试样双线性硬化模型拟合Fig.3 Bilinear model fitting of the parent steel sample
2 弯曲应力的解析计算
2.1 弯曲应力计算公式
弯曲切应力、径向应力和纵向应力分别记为σθ、σr和σz。推导弯曲应力计算公式时作如下假定:(1)钢板横截面在弯曲过程中保持为平面;(2)忽略材料的Bauschinger效应;(3)弯曲过程中弯角部分保持为圆弧状;(4)宽板变形为平面应变问题。
对于钢板拉伸外区,真应变

式中:r为外区某层的弯曲半径;ρ为应变中性层半径。
设弯曲前、后的板厚为t0和t,则弯曲变薄系数η=t/t0,根据塑性变形体积不变原理,弯曲应变中性层半径

式中:r0为弯曲后圆弧内径。显然η<1,即应变中性层相对于几何中间层发生内移。若材料本构关系模型为
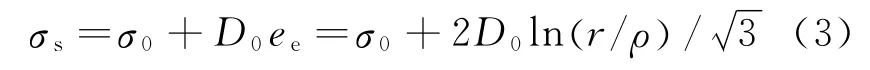
式中:σ0为外推流动应力;D0为材料硬化模数;ee为等效应变,根据母材双线性硬化模型参数的平均值,取σ0=400 MPa,D0=897 MPa。
弯曲平衡方程和塑性条件分别为
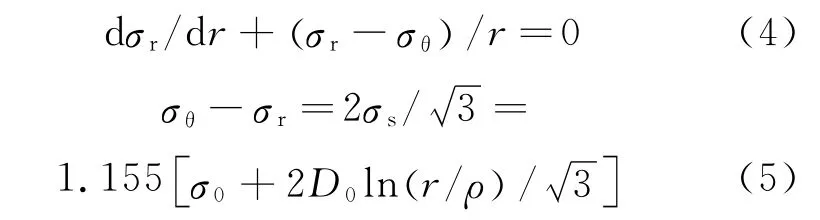
联立式(4)和式(5)进行求解,并考虑外区应力边界条件,即r=R时,σr=0,得到型钢冷弯外区应力:
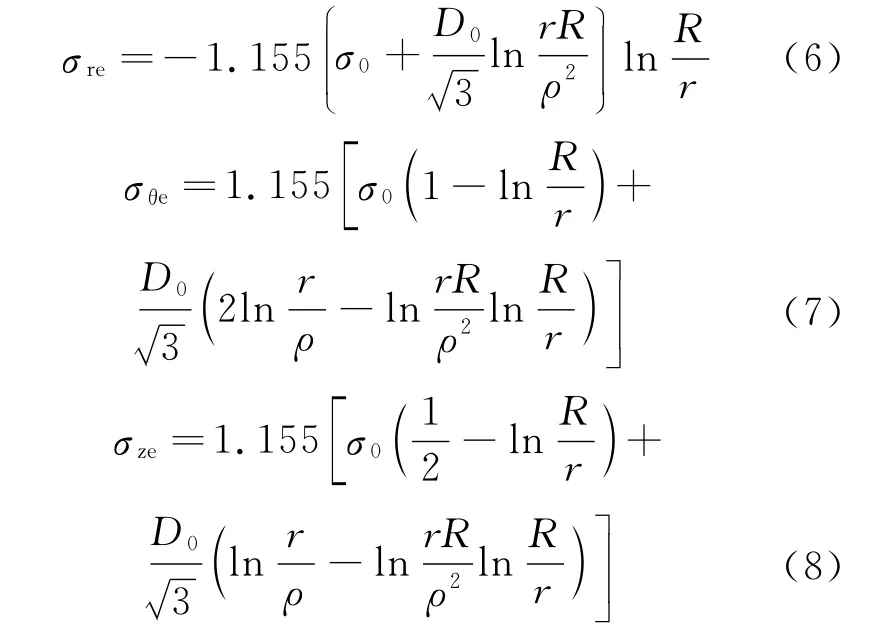
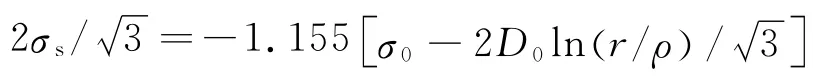

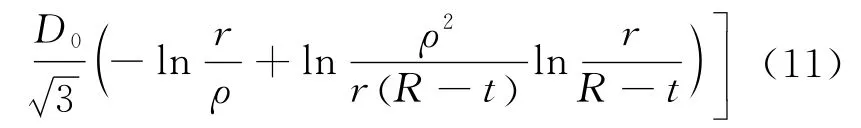
2.2 冷弯应力分布
定义相对弯曲半径Rt=(R-t)/t,Rt表示板材的弯曲程度,即随着(R-t)/t的减小,板材变形程度增大。化简式(6)~式(11)可知,对于给定材料,塑性弯曲应力仅与η和Rt有关。η和Rt满足(Rt+1)η=R/t0的关系,即随着弯曲的进行,Rt、η、R同时减小,且半径比厚度减小得更快。计算时取Rt=1.46,η=0.98,应变中性层内移0.36 mm,变形外区和内区的中性层应力分别使用r=1.01ρ和r=0.99ρ计算,得到考虑硬化的型钢冷弯应力分布如图4所示,图中σ—s为实测得到的母材平均屈服强度。
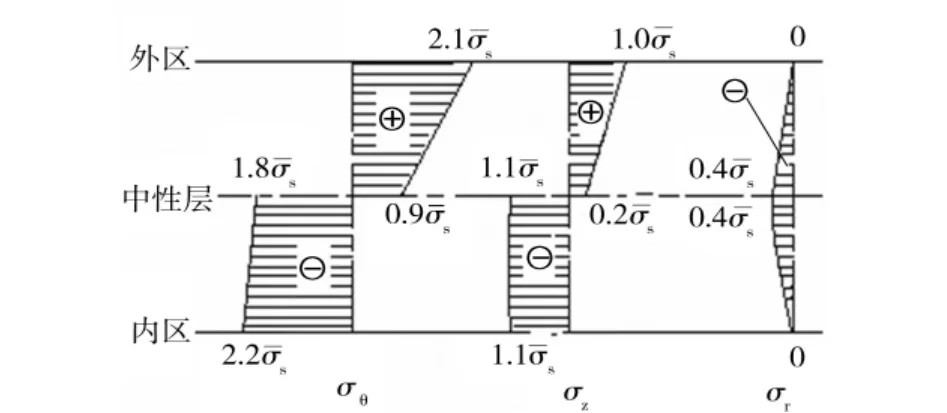
图4 沿壁厚方向的塑性弯曲应力分布Fig.4 Stress field at the cross section
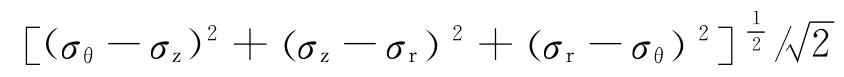
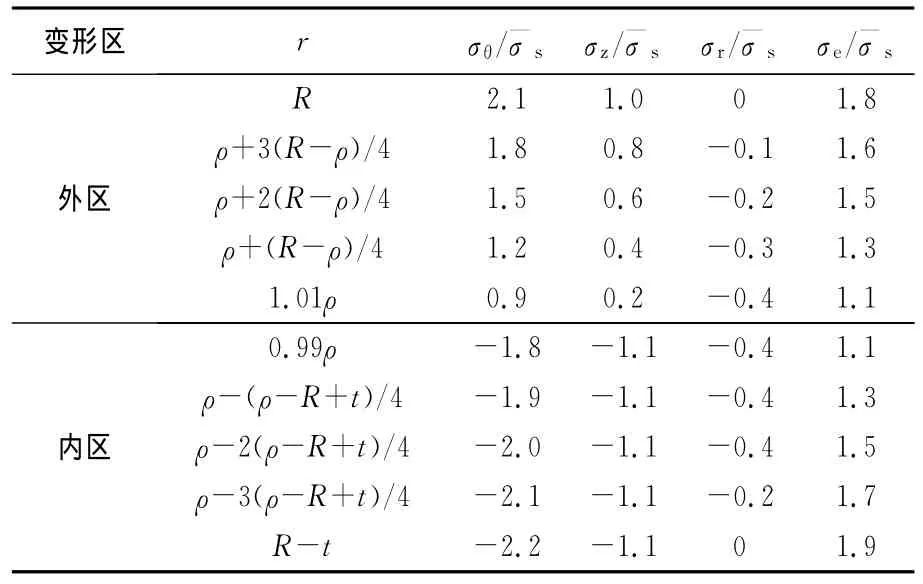
表3 等效应力计算结果Table 3 Results of effective stress calculation
3 回弹应力的数值模拟
3.1 几何模型与FEM模型
根据本文实测数据建立矩形钢管的几何模型,考虑对称性取其四分之一进行有限元分析。对型钢施加反向弯曲力矩来模拟回弹应力,根据式(12)计算弯曲力矩的大小,即沿轧件前进方向单位长度的弯矩
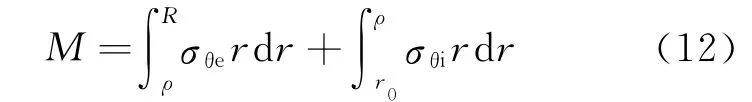
将回弹弯矩以集中载荷和分布载荷两种方式施加于弯曲段外的直边段上,其中集中载荷施于弯角和直边段的交界面上,而分布载荷沿交界面到板宽边缘线性分布。对端部简支约束,采用实体单元Solid45划分网格,得到回弹模拟FEM模型,如图5和图6所示。

图5 集中加载方式下的FEM模型Fig.5 FEM model at concentrated loading

图6 分布加载方式下的FEM模型Fig.6 FEM model at distributed loading
3.2 模拟结果与分析
采用ANSYS软件求解,得到两种加载方式下沿壁厚方向的冷弯型钢回弹应力场,如图7和图8所示。
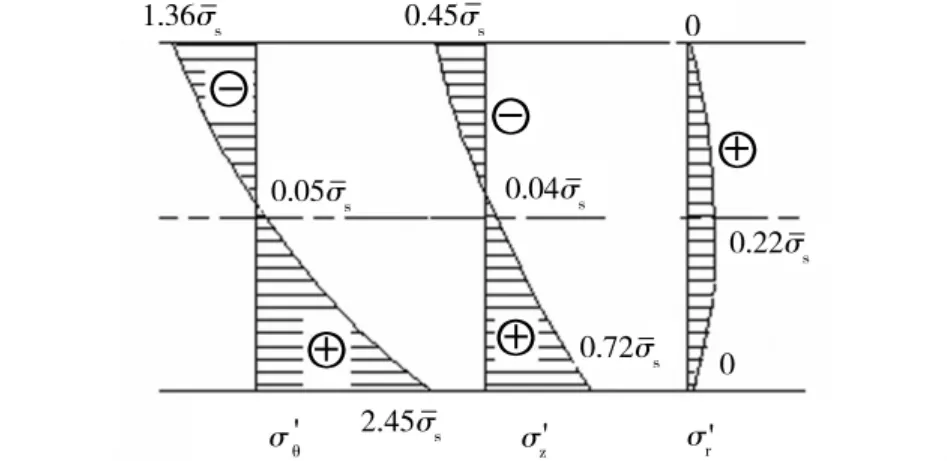
图7 集中加载方式下的回弹应力分布Fig.7 Rebound stress distribution at concentrated loading
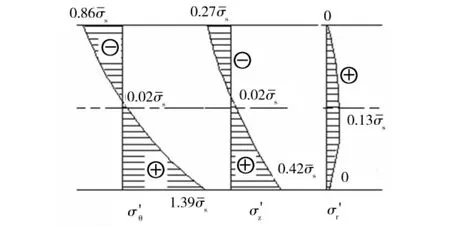
图8 分布加载方式下的回弹应力分布Fig.8 Rebound stress distribution at distributed loading
由图7和图8可见,两种加载方式下的弯角区回弹应力分布规律基本相同,但集中力加载时3个方向的回弹应力都较大。根据图7和图8中的数据,在截面上取3点进行等效应力计算,发现集中加载时回弹外区附近的等效应力大于弯角处实测平均屈服应力40%左右,表明外区附近材料进入塑性变形状态,这与回弹弹性变形计算相矛盾,再考虑到辊弯接触的实际状况,因此选择图8所示为回弹应力计算结果。
4 残余应力分布
将图4和图8中的计算结果进行代数值叠加,得到型钢截面残余应力分布,如图9所示。由图9可见,沿壁厚方向残余应力近似线性分布;与径向残余应力和纵向残余应力相比,切向残余应力较大,且最大值出现在中性层附近;径向残余应力为压应力,在拉伸区,切向和纵向残余应力为拉应力,其值沿外表面向中性层方向递减,在压缩区,切向和纵向残余应力为压应力,其值沿内表面向中性层方向递增;钢板内、外表面的纵向残余应力大小近似相等,约为材料屈服强度的70%。本文得到的残余应力方向和分布与文献[4]和文献[5]中给出的测量结果一致,表明文中所提出的厚壁型钢冷弯应力分析方法是合理的。
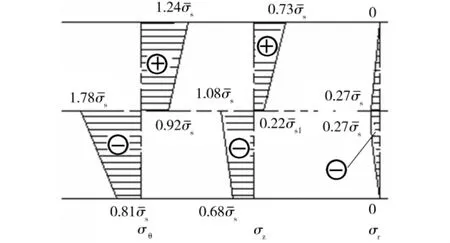
图9型钢截面残余应力分布Fig.9 Residual stress distribution at the cross section
5 结论
(1)冷弯应力中,切向应力最大。变形外区拉应力(切向应力和纵向应力)由钢板外表面向中性层递减,变化幅度较大,压应力(径向应力)由钢板外表面向中性层递增;变形内区压应力中,切向应力和径向应力变化幅度较小,纵向应力基本保持不变。材料全截面处于塑性变形状态,内区平均弯曲等效应力略大于外区平均弯曲等效应力。
(2)残余应力沿板厚方向近似线性分布。变形外区,切向和纵向残余应力为拉应力,径向残余应力为压应力;变形内区3个方向的残余应力均为压应力。切向残余应力较大,最大值出现在板带的中性层附近。
[1] 温东辉,沈祖炎,李元齐.冷弯厚壁型钢冷弯效应及残余应力研究进展[J].结构工程师.2010,26(1):156-163.
[2] Li S H,Zeng G,Ma Y F,et a1.Residual stresses in roll-formed square hollow sections[J].Thin-Walled Structures,2009,47(5):505-513.
[3] Hu Shengde,Ye Ben,Li Lixin.Materials properties of thick-wall cold-rolled welded tube with a rectangular or square hollow section[J].Construction and Building Materials,2011,25:2 683-2 689.
[4]Weng C C,Pekoz T.Residual stresses in coldformed steel members[J].Journal of Structural Engineering,1990,116(6):1 611-1 625.
[5] Weng C C,White R N.Residual stresses in coldbent thick steel plates[J].Journal of Structural Engineering,1990,116(1):24-39.
Stress analysis of thick-wall cold-bent profiled steel
Hu Shengde,Liu Yong,Jia Yuchao,Huang Caizhi,Song Gaowei,Wang Fan,Zhao Wenjing
(Key Laboratory for Ferrous Metallurgy and Resources Utilization of Ministry of Education,Wuhan University of Science and Technology,Wuhan 430081,China)
With a kind of rectangle thick-wall steel pipe as the research object,the plastic bending stress distribution of the thick-wall steel in the cross section was analyzed on the basis of strain hardening test.Mathematical simulation was carried out of the cold-bending rebounding stress,and the residual stress of the steel in the cross section was calculated by adding the cold-bending stress and the rebounding stress.The result indicates that the positive tangential stress and longitudinal stress decrease rapidly from outer surface to neutral layer,and the longitudinal stress in compression zone changes slightly.The residual stress is distributed in the cross section roughly linearly.The largest tangential residual stress lies close to neutral layer.The result agrees with that in the references published.
cold-bent thick-wall profiled steel;residual stress;hardening;finite element method
TG335.1
A
1674-3644(2012)03-0174-05
[责任编辑 尚 晶]
2011-11-17
武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室开放基金资助项目(FMRU2007Y01).
胡盛德(1972-),男,武汉科技大学副教授,博士.E-mail:adhello@163.com

