农产品物流运输网络优化设计

武汉工业学院经济与管理学院 李庆芳

1 在农产品物流中构建轴辐式网络的必要性和可行性

1.1 轴辐式网络的基本理论

根据物流节点性质的差异性，物流网络可分为完全连通的物流网络和轴辐式物流网络，在完全连通的物流网络中，物流节点不存在差异；但是轴辐式物流网络包括枢纽点和非枢纽点，非枢纽点之间通过枢纽点进行连接，而枢纽点之间形成了规模效益。图1和图2分别是完全连通物流网络和轴辐式物流网络。

图1

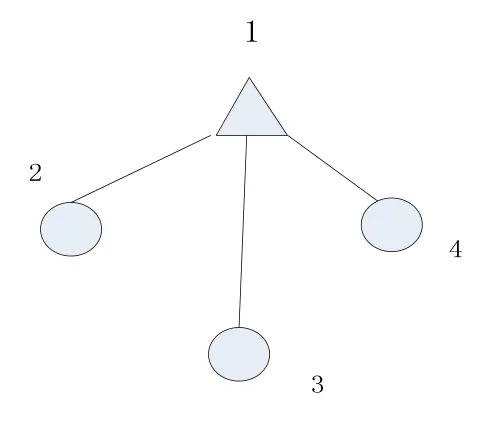
图2

轴辐式网络最初被应用于航空业的航空节点布局中，由于其规模效应，轴辐式网络逐渐被推广到其他领域，同时，国内外学者对轴辐式网络进行了广泛的研究，主要集中在网络的应用研究以及对轴辐式网络的优化分析等方面[1]。翁瑞克[2]通过建立成本-路线优化模型以及中位问题模型来分析轴辐式网络的优化问题；柏明国[3]将启发式算法应用在了轴辐式物流网络的模型求解中；Marcos & Cunha[4]解决了单分配枢纽模型求解过程中出现多初始解的问题。

1.2 在农产品物流中构建轴辐式网络的必要性和可行性

轴辐式网络具有聚集效应，可以提升规模经济，我国农产品物流成本占农产品成本的比例较高，而在农产品物流成本中运输成本占比较高，在农产品物流中应用轴辐式网络，可以有效提升规模经济，降低运输成本。

另外，在农产品物流中构建轴辐式网络也是可行的，主要体现在以下几个方面：第一，农业中大量的农户以及分散的客户可以看做轴辐式网络的非枢纽点，农贸市场或者农产品聚集地和分散地可以看作轴辐式网络的枢纽点，符合轴辐式网络的应用情景；第二，农产品往往都是通过农贸市场集散，所以农贸市场的选址极为重要，而枢纽点的选择正是轴辐式网络要解决的首要问题。

2 农产品物流的轴辐式运输网络模型

构建农产品物流的轴辐式运输网络的目标是使运输成本最低，假设一个非枢纽点只能和一个枢纽点相连，则可以构建农产品运输的单分配多枢纽问题模型。

2.1 参数设置

以下图所示的轴辐式网络为情景，其中m为农户，n为顾客，为非枢纽点，i为农产品聚集地，j为农产品发散地，为枢纽点。

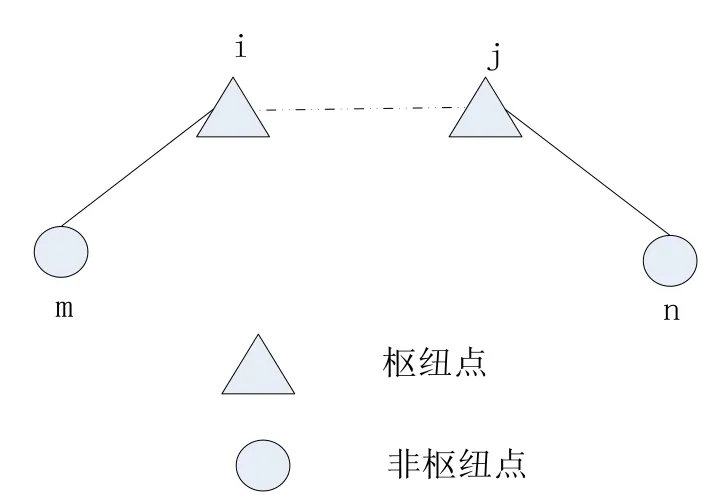
图3 轴辐式网络情景

Om:农户m卖出的农产品的总量Dm:顾客n买到的农产品的总量

2.2 单分配多枢纽中位问题模型

该模型建立的目的是在选取合适的农产品聚集地和发散地的位置，使运输成本最小化，假设下列条件：

(1) 在农产品物流网络中共有n个节点，选取p个枢纽，枢纽即为农产品聚集地和发散地；

(2) 农业聚集地和农业发散地之间能够完全连同，但是农户和顾客之间只能通过农业聚集地和农业发散地进行连接

(3) 农户具有固定的卖家，顾客经常固定去某个地点购买农产品；

(4) 枢纽城市之间的单位运输成本又一个成本折扣α，由于农产品聚集地和农业发散地之间具有大量的农产品流动，所以单位运输成本存在一个折扣系数α，0<α<1；

农户的生产量以及顾客的购买量均没有限制。

在上述条件下，从n个地点中选取p个来监理农产品聚集地和农产品发散地，模型如下；

其中，运输成本包含农户到达农产品聚集地的运输成本、农产品聚集地到农产品发散地的运输成本以及顾客到达农产品发散地的成本，假设农户到达农产品聚集地以及顾客到达农产品发散地具没有折扣，而农产品聚集地到达农产品发散地由于流量大，所有具有折扣α。

式子（1）表示需要建立p个农产品聚集地和发散地；式子（2）表示农户具有固定的卖家，顾客经常固定去某个地点购买农产品；式子（3）、（4）表示农户发出的农产品经过农产品聚集地和发散地到达顾客；式子（5）表示农户具有固定的卖家，顾客经常固定去某个地点购买农产品。

3 农产品物流轴辐式运输网络的算例分析

本章主要应用禁忌搜索算法来对该模型进行求解，并进行实证说明。

3.1 禁忌搜索算法介绍

管理工程的模型求解可以有多种算法， 所有算法的目的都是通过建立一定的计算规则来对模型进行求解。在传统的启发式算法中，由于算法本身的局限，只能求得局部最优解，而现代人人工智能算法能够提高计算过程的深度和广度，从而得到最优解。禁忌搜索算法即为一种人工智能算法，可以高速的处理模型问题。

禁忌搜索算法的基本原则是在找到局部最优解后，通过构建解的评价函数，来跳出局部循环，使得再次进行搜索时候能够避开已经得到的局部最优解，从而找到真正的全局最优解，。算法的基本步骤是（1）找到一个初始可行解；（2）通过交换方法对初始可行解的邻域进行搜索，如果新找到的可行解优于初始可行解，那么将把该局部最优解记录在禁忌表，邻域是指根据交换、插入等移动策略而在现有解的基础上形成的新解的集合；（3）继续进行搜索，并且跳过已经记录在禁忌表中的局部最优解，禁忌表是存放禁忌解的空间，存放于禁忌表中的解在下次搜索时均不会被再搜素到；（4）利用禁忌长度或者其他的停止准则来停止禁忌搜索算法的求解过程，得到真正的全局最优解。

3.2 算例分析

本算例的目的是在农产品物流节点中选取几个枢纽点构建轴辐式运输网络，达到运输成本最小化的目的。本文选择文献[5]中的距离矩阵和流量矩阵作为成本矩阵和流量矩阵，首先对两个矩阵的元素进行相乘处理，得到成本-流量矩阵，然后结合JAVA编程来实现禁忌搜索算法的求解。

设置为禁忌长度为8，成本折扣系数选取0.4、0.6、0.8，当可选的节点个数分别为15和20的时进行枢纽点的选择，枢纽点分别选3和4，停止准则为当最大迭代次数为50次或者连续三次得到相同的最优解时停止搜索运算。

最优解数据如下表1所示：

表1 最优解数据

从表中可以看出，当节点总数为15时，并且选取3个点作为农产品聚集地和发散地，并且折扣系数为0.4时可以得到最优解。

综上所述，禁忌搜索作为一种智能算法，可以有效的应用在农产品物流网络模型的构建中，并且相对于传统的算法，其运算速度更为快捷。同时，还可以不断的调整其中参数的设置，来处理各种不同的情况，所以具有广泛的适用性。

4 结语

首先，本文阐述了在农产品物流中构建轴辐式网络的必要性和可行性，由于降低农产品成本的迫切性以及农产品物流情景和轴辐式网络的匹配性，在农产品物流中构建轴辐式网络是必要的，而且可行的；其次，构建了农产品物流轴辐式网络的单分配多枢纽中位问题模型；最后，用禁忌搜索算法对模型进行了求解，事实证明禁忌搜索算法可以很好的应用在求解单分配多枢纽中位问题的过程中，而且也证明了在农产品物流中构建轴辐式网络的经济性。

[1]李阳.轴辐式网络理论及应用研究[D].上海:复旦大学,2006.

[2]翁克瑞.轴辐式物流网络设计的选址与路线优化研究[D].武汉:华中科技大学,2007.

[3]柏明国.基于禁忌搜索算法的枢纽航线网络优化设计研究[J].经济数学,2008,25(4).

[4]Marcos RobertoSilva＆ClaudioB.Cunha.New simple and efficient heuristics for the uncapacitated single allocation hub location problem[J].Computers & Operations Research,2009(36).

[5]柏明国.航空公司航线网络优化设计问题研究[D].南京:南京航空航天大学,2006.