超声散射CT信号的特征提取
张蕾,宋文爱,杨顺明
(1 中北大学信息与通信工程学院, 山西太原 030051; 2 中北大学软件学院,山西太原 030051)
0 引言
超声散射CT边界信号是一种典型的瞬态信号。采用传统的傅里叶分析方法得到的频谱,无法同时反映出其时域突变位置和对应频率等特征信息,而边界信号的特征提取和选择却是边界分类的前提,因此,特征提取方法的优劣直接影响着边界分类的正确性和可靠性[1]。希尔伯特-黄变换(Hilbert-Huang Transform,简称为HHT)是由美籍华人Norden E.Hang等人于1998年提出的[2]。这一方法是一种全新的信号处理方法,对于处理非线性、非平稳信号有清晰的物理意义,够得到信号的时间-频率-能量分布特征,且是一种自适应性信号处理方法[3]。小波变换由于具有时频分辨率高和多分辨率分析的特点,适用于对瞬态信号的处理,已被广泛用于超声信号的特征提取。本文拟通过对荷兰试块3个不同的检测面使用HHT及小波包进行能量特征提取,采用基于距离的类别可分性判据对两种方法的提取结果进行可分性测度分析,对比实验结果。
1 实验系统及实验数据
图1为所研究的检测对象钛合金CSK-IA型试块。图中标出了试块的尺寸、阵列传感器布置区域及阵元编号。阵列传感器A具有49个阵元,阵元宽度为1 mm。传感器频率为6.25 MHz,在被检试块中的波长近似为1 mm。图中虚线框所标成像区域I对应阵列传感器A的成像区域,界面1-6为可能引起散射的界面。界面1为半径100 mm的圆弧界面,界面2为深度91 mm的水平界面,界面3为高度为6 mm的竖直界面,界面4为深度85 mm,宽度2 mm的水平界面,界面5为高度15 mm的竖直界面,界面6为深度100 mm的水平界面。
本文对界面2、界面4、界面6产生的信号分别进行EMD分解和小波包分解进行能量特征提取。界面2、界面4、界面6的一维压缩图像如图2所示。

图1 超声散射CT的钛合金CSK-IA型试块及探头阵列布设
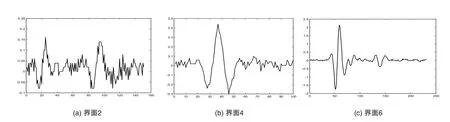
图2 一维压缩图
2 特征提取
2.1 基于HHT的能量特征提取
超声散射CT信号具有非平稳性。基于EMD(empirical mode decomposition)的HHT(Hilbert-Huang transform)是分析非线性、非平稳信号的一种方法[4-6]。它的特点是通过EMD对非线性、非平稳数据进行线性和平稳化处理,得到IMF(intrinsic mode function)分量,并在分解过程中保留数据本身的特性。该方法具有小波变换多分辨的优点,同时又克服了小波变换中小波基选取的困难。它从信号本身的尺度特征出发对信号进行分析,能尽快地分析出信号的特征,具有良好的局部适应性[7]。
本文对界面2、界面4、界面6产生的信号进行基于EMD分解的HHT变换,得到EMD分解结果如图3所示。其中S(t)为原信号,imf表示IMF分量,r表示分解的剩余量。

图3 EMD分解
从图中可以清楚地看到:通过EMD分解可以将界面信号的IMF分量按频率由高到低的顺序依次分离出来,很好地展示了界面信号的频率分量成分。通过比较图3中的(a)(b)(c),可以发现不同界面的信号经EMD分解后得到的IMF分量个数是不固定的,经过大量的实验数据验证得知,信号经EMD分解后的IMF分量为5到7个不等。本文将界面信号定为经EMD分解后得到5个IMF分量加1个r分量,即信号经EMD分解后IMF分量多于5个的都加到r分量上作为1个r分量,然后对上述6个分量作Hilbert变换,提取IMF能量作为特征向量。
对每一个IMF作Hilbert变换后得:

这里省略了残余函数r,Re代表取实部。式(1)称为Hilbert幅值谱。简称Hilbert谱,记为:

以上的EMD以及相应的Hilbert谱信号的分析方法统称为基于EMD的Hilbert变换,亦称为HHT。为了利用HHT方法识别界面,现定义分解后各模态能量为:

最后对能量进行归一化处理。通过数据验证知,选取各IMF能量和r能量也可简单地把界面给区分出来,如图4所示。可以看出界面2信号的r能量远大于其他界面信号的r能量。另外,根据信号的主要分布频带:界面2的能量主要分布在第3、4频带,界面4的能量主要集中在第2频段,界面6的能量主要集中在第1频段,也可初步将界面区别开。

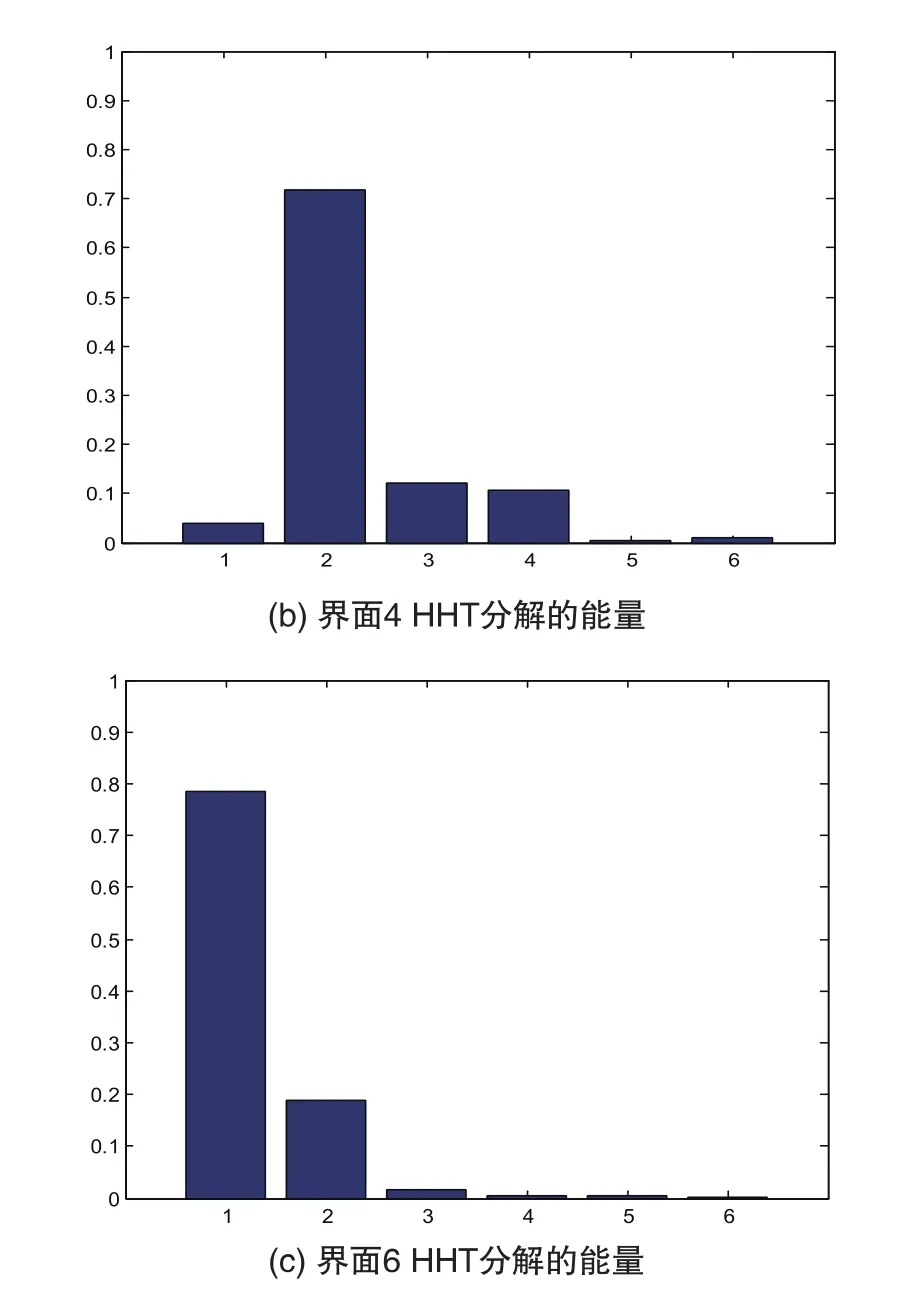
图4 区分后的界面
2.2 基于小波包变换的能量特征提取
在超声检测过程中,如果材料出现缺陷,超声回波信号的幅频特性就会出现不同程度的改变:某一些频段内信号能量增强,另一些频段内信号能量则会减小。因此,在信号的各频率成分能量中,包含着丰富的缺陷信息,某种或几种频率成分能量的改变就代表着一种缺陷情况[8]。所以,可以采用将小波包多分辨率分析与各频段能量相结合的信号特征提取方法,对本实验不同界面的超声散射CT信号进行特征提取。
经实验比较后,选用Daubechies8小波作为小波函数,选取分解层数为3层对采样信号进行小波包分解,得到3层8个频带的小波包分解系数,再对其进行重构。
对界面超声信号S(t)进行3层小波包分解,得到小波包分解序列S3j=(j=0, 1, …, 7),则各频带信号对应的能量E3j为:

总能量E为:

其中, xjk(j =0,1,… ,7;k=1,2, …,n)表示重构信号S3j的离散点的幅值[9]。最后对能量进行归一化处理。界面信号小波包分解的能量如图6所示。
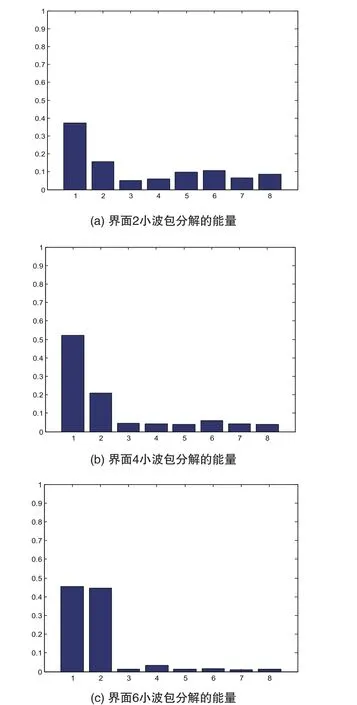
图6 小波包分解的能量
由图6可以看出,不同界面的超声散射CT信号经小波包分解后,其能量在各频带上的分布是不同的,且其能量值也有差别,可以简单将界面区分开来。很显然,界面4在第1和第2频带的能量值都比较大。因此,可将小波包分解的能量看作不同界面的特征值,作为后续缺陷分类的依据。
3 类别可分性判据
超声散射CT信号的特征提取是边界定性识别的前提和关键,选取有效的特征值对提高识别的正确率起着关键作用。特征提取的方法有很多种,因而就需要对信号提取的特征值进行评价。可分性测度可作为衡量不同类间可分性的一个指标,越大表示可分性越好。相对于相同的分类器来说,好的类间可分性能够使分类器的识别率得到显著提高;而较为混杂、互相交叉的特征信息则会使分类器的模式识别变得非常困难[10-11]。
本文选用基于距离的类别可分性判据方法对上文EMD分解和小波包分解提取的能量特征进行可分性测度计算,计算结果如表1和表2 所示。

表1 EMD分解的能量特征进行可分性测度分析

表2 小波包分解的能量特征进行可分性测度分析
从表1和表2可以看出,3种界面的EMD分解和小波包分解的能量特征可分性测度平均值分别为0.4167和0.4375,这表明基于EMD分解的HHT变换虽然具有小波变换多分辨的优点,同时又克服了小波变换中小波基选取的困难,但对于本实验中信号频率成分比较单一的信号,小波包分解提取的能量特征比EMD分解提取的能量特征更为有效。
[1]李功,黄民.基于小波包变换的超声回波信号特征提取[J].合肥工业大学学报:自然科学版,2006,29(2):246-249.
[2]Huang N E,Zheng S,Long S R,et a1.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London,Series A,1998,454:903-995.
[3]黄诚惕.希尔伯特-黄变换及其应用研究[D].成都:西南交通大学,2006.
[4]黄海,黄轶伦.气固流化床压力脉动信号的Hilbert-Huang谱分析[J].化工学报,2004,55(9):1441-1447.
[5]孙斌,张宏建,岳伟挺.HHT与神经网络在油气两相流流型识别中的应用[J].化工学报,2004,55(10):1723-1727.
[6]王晓萍.三固流化豪压力信号的Hilbert-Huang变换与流型识别[J].高校化学工程学报,2005,19(4):474-479.
[7]周云龙,王强,孙斌,等.基于希尔伯特-黄变换与Elman神经网络的气液两相流流型识别方法[J].中国电机工程学报,2007,27(11):50-56.
[8]张冬雨,刘小方,杨剑,等.基于小波包变换的复合材料分层缺陷信号特征分析[J].兵工自动化,2009,28(11):56-58.
[9]师小红,敦怡,徐章遂,等.基于“能量-缺陷”的金属基复合材料缺陷信号特征提取[J].计算机测量与控制,2006,14(1):109-122.
[10]刘旭.超声探伤缺陷分类中信号处理方法及系统的研究[D].北京:中国矿业大学,2000.
[11]刘旭,夏金东,吴淼.超声检测缺陷分类的降噪及特征提取问题研究[J].中国矿业大学学报:自然科学版,2001,30(3):248-251.

