磁悬浮永磁直线电机伺服系统H∞鲁棒控制的研究*
蓝益鹏,韩晓明
(沈阳工业大学电气工程学院,沈阳 110870)
磁悬浮永磁直线电机伺服系统H∞鲁棒控制的研究*
蓝益鹏,韩晓明
(沈阳工业大学电气工程学院,沈阳 110870)
磁悬浮永磁直线电动机具有直接驱动与磁悬浮的特点,它能消除传动链所带来的不良影响以及动子与静止导轨之间的摩擦,提高系统的快速反应能力和精度。针对磁悬浮永磁直线电动机中的不确定性扰动,提出基于黎卡提不等式(Riccati)方法设计进给系统的H∞鲁棒控制器。首先,采用矢量控制方法中的id=0控制策略,把非线性系统解耦成独立的线性电流子系统和速度子系统。其次,在建立系统状态空间模型的基础上,将此系统归结为标准的H∞控制问题,通过求Riccati不等式的对称正定解,进而得到磁悬浮永磁直线电动机系统的状态反馈H∞控制器。最后,在MATLAB环境下搭建系统的仿真模型,对控制系统进行仿真研究,结果表明所设计的H∞控制器满足对不确定性扰动抑制的要求。
磁悬浮永磁直线电动机;鲁棒控制;Riccati不等式
0 引言
现代制造技术正朝着高速化、精密化和模块化方向发展[1]。在传统的工业控制中,皆以“旋转电机+滚珠丝杠”作为驱动机构实现数控机床的直线形式运动。由于这种机构中存在中间环节,因而大大降低了系统的机械刚度,同时使得系统的速度和加速度过分受限于机械因素[2-3]。虽然永磁直线伺服系统具有进给调速范围广、加速度大、速度特性好、行程不受限制、定位精度高等诸多优点,但由于其取消了全部中间环节,负载的变化和外部的扰动将直接作用于伺服系统本身,这严重影响了系统的性能,特别是难以克服摩擦对系统产生的不利影响。
磁悬浮永磁直线同步电动机兼有永磁电动机和直线电动机的双重优点,并具有非接触 、无摩擦、无磨损、环保等特点。总体性能上具有较大优势,在数控机床中具有广阔的应用前景。然而,磁悬浮永磁直线同步电动机控制系统是一个多变量、强耦合的非线性系统[4-5],它不同于直流旋转电动机可以分别控制励磁控制回路和转矩控制回路,这就增加了控制上的难度。
针对控制对象的不确定性,H∞控制作为非常有效的方法,对抑制扰动具有良好的效果。在H∞鲁棒控制器设计中,采用了Riccati不等式的处理方法,通过求Riccati不等式的对称正定解,进而求得控制器,使系统具有较强的鲁棒性。
1 磁悬浮永磁直线同步电动机的状态空间模型
磁悬浮永磁直线电动机的动子上有两套电气上相互独立的绕组,一套绕组是用于产生电磁推力的推力绕组,另一套绕组是用于调节磁悬浮力的悬浮绕组,专门用于对气隙磁场进行调节,从而改变磁拉力的大小,使永磁直线电动机靠自身产生的磁悬浮力来运行。使数控机床进给平台在直接驱动的同时能够从根本上消除摩擦实现无摩擦进给[6]。
推力绕组中通入三相对称的正弦交流电流,采用id=0的控制策略,使推力绕组产生最大推力。在悬浮绕组中通入三相对称的正弦交流电流,采用iq=0的控制策略,以使悬浮绕组产生可控悬浮力。
假定d,q轴电感Ld=Lq=L。此时动子的电磁推力表达式为:

磁悬浮永磁直线电动机的动子处于悬浮状态,与导轨之间无摩擦,其机械运动方程为:
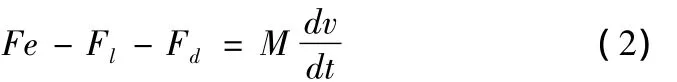
式中Fl负载阻力,M为动子质量,Fd为端部效应力,Kf为电磁推力系数,v为动子线速度。由分析和实验得到端部效应力简化数学模型为:
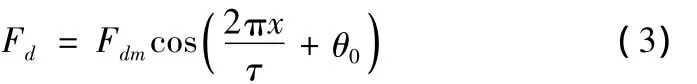
式中Fdm为端部效应力波动的幅值,τ为极距,x为动子的直线位移,θ0为与直线电机、定子电磁结构有关的常数。
在此情况下,磁悬浮永磁直线同步电动机的数学模型可描述为:
其中:uq,iq分别为q轴动子电压和电流,ψf为永磁体基波励磁磁链,Rs为动子电阻,np为极对数。
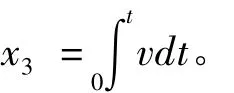
2 H∞鲁棒控制器设计
用H∞控制理论设计控制系统,不论是鲁棒稳定还是干扰抑制问题,都可以归结为求解反馈控制器,使闭环系统稳定,并且从扰动输入w到被调输出z的闭环传递函数阵的H∞范数最小或者小于某一给定值(次优化问题)[7]。
为此,将以上的线性系统控制归结为标准的H∞控制问题,考虑广义被控对象的状态空间实现为:
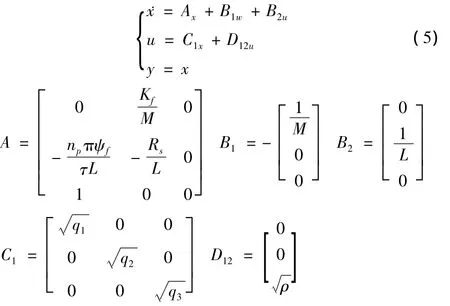
其中 qi≥ 0,i=1,2,3;ρ> 0,为加权系数。D12列满秩,(AB2)可稳定。即:

对系统(5)要求设计反馈状态控制器:

定理1[7]:对于给定的γ>0,存在状态反馈阵K使得闭环系统(6)和(7)内部稳定且:

成立的充分必要条件是存在正定阵X>0,满足Riccati不等式:

若上述不等式有正定解X>0,则使闭环系统稳定且式(8)成立的状态反馈阵由下式给出:
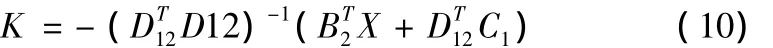
利用MATLAB求解式(9)、(10)即可求得需要的控制器K。
3 仿真研究
在MATLAB的仿真环境下,搭建了采用id=0的矢量控制的系统状态反馈仿真模型。其中ks为位置控制器,k=[k1k2k3]为H∞控制器。如图1所示。
系统的仿真参数如下:
M=50kg,Rs=1.6878Ω,L=25.92mH,τ=33mm,np=3,ψf=0.1754Wb,等效的电流控制器增益ki=300,位置控制器ks=7.5。加权系数:q1=159.2,q2=2005.99,q3=6.4865;ρ=0.0923。

其中状态反馈阵求得为:
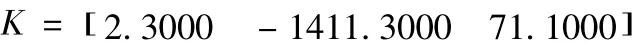

图1 系统状态反馈仿真模型
通过对系统进行仿真,在没有扰动信号和扰动信号为阶跃信号情况下分别对状态变量:电流iq,速度v,位移s进行跟踪,得到研究结果如图2至图4所示。

图2 阶跃扰动下位移信号跟踪响应曲线
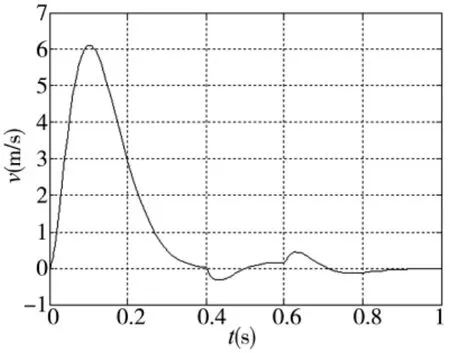
图3 阶跃扰动下速度信号跟踪响应曲线

图4 阶跃扰动下电流信号跟踪响应曲线
在有扰动信号的情况下,在t=0.4s时突加载幅值为F=25N的负载扰动,在t=0.6s卸去扰动,从图中可知系统对扰动信号具有良好的抑制特性。
4 结论
(1)在建立磁悬浮永磁直线电动机状态空间模型的基础上,将此系统归结为标准的H∞控制问题,通过求Riccati不等式的对称正定解,进而得到磁悬浮永磁直线电动机系统的状态反馈H∞控制器。
(2)建立了磁悬浮永磁直线电动机控制系统的仿真模型,对其进行了仿真研究,结果表明基于Riccati不等式设计的磁悬浮永磁直线电动机控制系统具有良好的跟踪性能和对干扰的抑制性能。
[1]王先逵,陈定积,吴丹.机床进给系统用直线电机综述[J].制造技术与机床,2001(8):18-20.
[2]宁建荣,夏加宽,沈丽.PMLSM直接驱动工作台的机电耦合有限元建模[J].沈阳工业大学学报,2011,33(6):618-622.
[3]黄伟忠,宋春华.永磁交流伺服电机国内外市场概况[J]. 微特电机,2009,37(1):59-62.
[4]叶云岳.直线电机原理与应用[M].北京:机械工业出版社,2000.
[5]田录林,张靠社,王德意,等.永磁导轨悬浮和导向磁力研究[J]. 中国电机工程学报,2008,28(21):135-139.
[6]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,1997.
[7]申铁龙.H∞控制理论及应用[M].北京:清华大学出版社,1996.
Robust Control Research for Magnetic Levitation Permanent Magnet Linear Motor Servo System
LAN Yi-peng,HAN Xiao-ming
(School of Electrical Engineering,Shenyang University of Technology,Shenyang 110870,China)
The magnetic levitation permanent magnet linear motor is direct drive and magnetic,it can eliminate some adverse effects caused by the transmission chain and the friction between the mover and the static guide,greatly improve rapid response capability and motion precision.Aiming at the uncertainty disturbance of magnetic levitation permanent magnet linear motor,an H∞robust controller for driving system based on Riccati inequality was proposed.First,the id=0 method which is one of vector control’s methods is used for decoupling the nonlinear system to unattached linear current subsystem and speed subsystem.Second,on the basis of building the system state space model the synthesis of linear servo system is converted into a standard H∞control problem,through solving an algebraic matrix Riccati inequality with symmetrically positive solution,after that state feedback H∞controller for magnetic levitation permanent magnet motor system is acquired.Finally,a simulation model is conducted under the MATLAB condition,study on simulation for the control system is made.The simulation indicated that the H∞controller could achieve the design target and have excellent uncertainty disturbance attenuation performance.
magnetic levitation permanent magnet linear motor;robust control;Riccati inequality
TH122;TM383.4
A
1001-2265(2012)11-0061-03
2012-03-22
国家自然科学基金资助项目(50975181)
蓝益鹏(1962—),男,陕西华县人,沈阳工业大学电气学院副教授,博士,硕士生导师,主要从事数控技术、鲁棒控制的研究等,(E-mail)lanyipengg@163.com。
(编辑 李秀敏)

