高速铣削P20模具钢表面粗糙度预测模型研究

陈锦江，龙 超，王 超

(燕山大学机械工程学院，河北秦皇岛 066004)

高速铣削P20模具钢表面粗糙度预测模型研究

陈锦江，龙 超，王 超

(燕山大学机械工程学院，河北秦皇岛 066004)

正交试验法分析了高速铣削P20模具钢时铣削速度、每齿进给量、铣削深度和行距等参数对表面粗糙度的影响。采用回归分析方法建立表面粗糙度预测模型，用方差分析验证了该模型的显著性和可靠性。

高速铣削;表面粗糙度;预测模型;P20模具钢

0 引言

高速切削是近些年来迅速崛起的一项先进制造技术，如今已经成为提高加工质量和加工效率、降低成本的重要途径［1］。

表面粗糙度是高速精加工中衡量加工表面质量的一个重要技术指标，是切削参数和系统变量对整个切削过程影响的综合反映［2］，其大小直接影响着机器的使用性能。然而高速切削时表面粗糙度的形成机理还不成熟，尚未建立完整的切削参数数据库。许多工艺人员不得不依靠经验公式或查阅手册来确定切削参数，往往因数值保守而达不到精度要求，甚至会破坏机床的安全性，使高速切削的优越性不能得到充分发挥。为此有必要通过试验建立精度和可靠性均较高的表面粗糙度预测模型，在实际加工前对表面粗糙度进行合理预测，以便于确定合理的切削工艺方案。

1 表面粗糙度试验研究

1.1 正交试验方案设计

研究表面粗糙度的试验方法通常有2种:单一因素法和多因素法。单一因素法对第一个因素的起点依赖性很大，多因素组合试验是将多个需要考察的因素通过数理统计原理组合在一起同时试验，而不是一次只变动一个因素，因而有利于揭示各因素间的交互作用，并且多因素正交试验可以减少试验次数。本文采用多因素正交试验法进行研究。

正交试验法(orthogonal experimental)是一种科学地设计与分析多因素试验的高效率的试验设计方法［3］。为了充分考察铣削过程中表面粗糙度与铣削参数的关系，采用正交试验法以铣削速度、每齿进给量、铣削深度、行距为影响因素，以工件表面粗糙度为考察指标。选定的因素水平如表1所示。

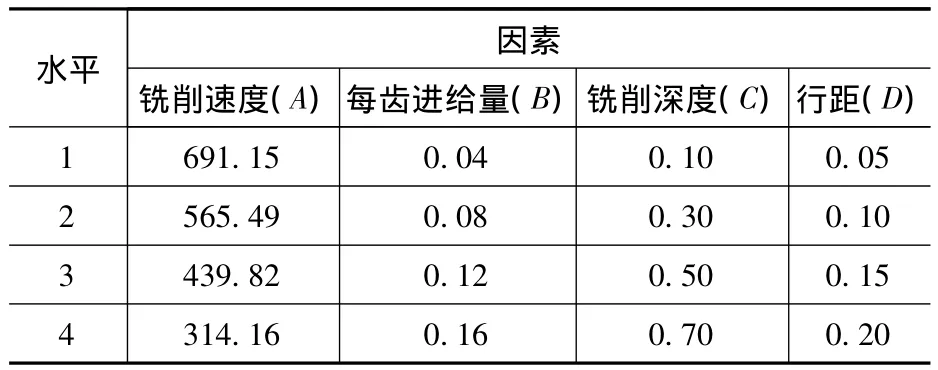
表1 因素水平表

1.2 试验条件

试件材料选用P20模具钢，硬度是36～40HRC，其综合力学性能好、具有良好的抛光性能，能避免热处理时引起的模具变形。机床为DMG公司的五轴数控加工中心，主轴最高转速24000r/min。采用OSK系列整体式硬质合金球头铣刀，铣刀齿数2，刀具直径为10mm。测量仪器选用Taylor Hobson接触式表面粗糙度测量仪。

考虑到试验费用及成本，加工方式为精铣平面表面，每次加工后用接触式表面粗糙度仪重复测量3次。

试验方案选用五因素四水平正交表，试验结果如表2所示。

表2 表面粗糙度试验方案设计及试验结果

1.3 数据处理

极差分析法又称直观分析法。它具有计算简便，直观形象，简单易懂等优点，是正交试验结果分析较常用的方法。通过对试验数据的计算、分析可以得到各因素对考察指标影响的主次顺序，最优方案以及考察指标随因素变化的规律。

极差值越大，说明该因素对试验考察指标就越重要，从而可以依据极差的大小判断因素影响表面粗糙度的主次顺序，极差分析表如表3所示。

表3 极差分析表

1.4 铣削参数对表面粗糙度的影响

分别以铣削速度、每齿进给量、铣削深度和行距为横坐标，加工后零件表面粗糙度的数值为纵坐标，结果如图1。

由图1a可知，随着铣削速度的增大，表面粗糙度随之降低。因为速度增大，被切屑带走的热量增多，传给工件的热量则大幅度减少，因而减小了加工零件的内应力和热变形;同时随着速度的增大，铣削力降低，铣削过程变得平稳。但当铣削速度达到565m/min后，机床振动加剧，表面粗糙度随铣削速度的增大而增大。

图1 表面粗糙度与各铣削参数关系图

由图1b可知，随着刀具每齿进给量的增大，表面粗糙度值总体呈增大趋势，说明进给速度越大，表面质量就越差。主要原因是进给速度增大使得在进给方向的残留高度变大。

由图1c可知，随着铣削深度的增加，表面粗糙度总体成增大的趋势，但增量不大，基本维持在一个相对较小的范围内。究其原因，轴向铣削深度对表面残留高度的影响是通过影响铣削力反应到工件表面上的，本试验铣削深度的取值并不大，所以对铣削力影响很小，则对表面粗糙度的影响就很弱。在进行精密铣削加工中，考虑到加工成本及加工效率，在已加工表面质量能够得到保证的前提下，应尽量选取较大的铣削深度。

由图1d可知，随着行距的增大，表面粗糙度值增大，且变化非常明显。主要原因是行距是工件残留高度的主要影响因素，行距越大，相应的残留高度越大，从而表面粗糙度值越大，加工表面质量就越差。但行距并不是越小越好，过小的行距使加工时间变长，影响加工效率。

2 表面粗糙度预测模型

2.1 表面粗糙度预测模型的建立

在高速铣削过程中，由于铣削速度、每齿进给量、铣削深度、行距等参数之间的尺度效应，目前，还很难得到这四个参数与表面粗糙度之间关系的定量的分析结论。

许多研究结果表明表面粗糙度与切削参数之间存在着复杂的指数关系，其通用形式［4］为:

两边分别取常用对数，将非线性函数转化成线性函数，即:

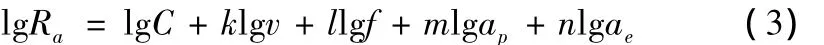
方程中的自变量与函数值之间存在着很好的线性关系，函数值用y表示，自变量用x1、x2、x3、x4表示，则多元线性回归的数学模型的结构形式如下:

式中，β0，β1，…βk为待估计的参数，ε1，ε2，…，εn服从正态分布N(0，σ2)的随机变量。

采用最小二乘法来估计参数 β。设 b0、b1、b2、b3、b4分别是参数 β0、β1、β2、β3、β4的最小二乘估计，则回归方程为:

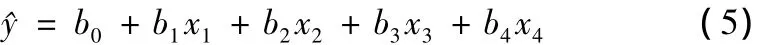
式中，b0、b1、b2、b3、b4为回归系数。

故高速铣削P20模具钢工件表面粗糙度的预测模型为:

2.2 显著性检验

为确保上述所建模型能够真实反映因变量与各自变量之间的变化规律，并应用到后续的参数优化中，在此对该模型进行显著性检验。

把总的偏差平方和分解成两部分，即回归平方和SA和剩余平方和SE。

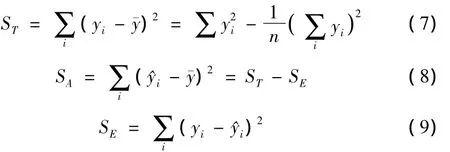
采用F检验法。对于某个因素A来说，FA称为A因素的F比，是一个自由度为(fA，fe)的F分布的随机变量。FA的计算公式为［5］:

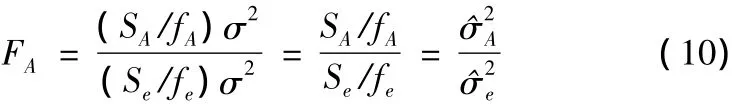
假设H0:β1=0，β2=0，β3=0，β4=0 可构造统计量:

相应的F值可根据公式求出，计算结果列于表4中。

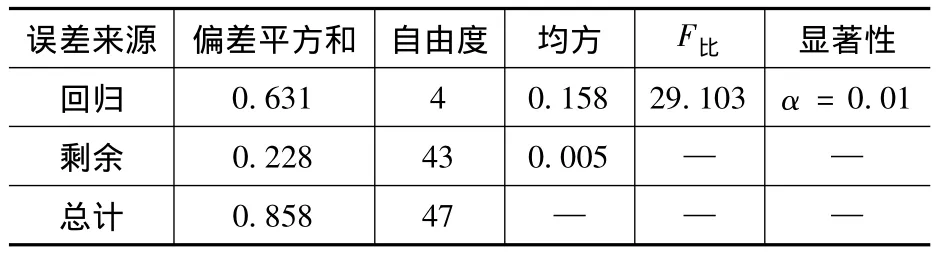
表4 回归方差分析表

查F分布表可知，F比＞F0.01(4，43)，故由F检验法可知高速铣削P20模具钢工件时表面粗糙度的回归方程是高度显著的。

2.3 表面粗糙度预测模型的验证

为验证表面粗糙度预测模型的预测精度，将实测值取平均值，与预测值的对比结果如图2所示。经计算可知Ra的预测误差为0.34% ～18.71%，表明该回归模型有较高的预测精度，可以对加工工件的表面粗糙度进行预测。

图2 表面粗糙度预测值与实测值对比

3 结束语

根据回归方程和回归系数的显著性检验以及试验结果分析，可得如下结论:

(1)通过试验建立了高速铣削P20模具钢的表面粗糙度预测模型，由回归方程及回归系数的显著性检验，证明了模型的高可信度。

(2)通过极差分析法分析试验数据，得到铣削速度(A)、每齿进给量(B)、铣削深度(C)和行距(D)对表面粗糙度影响程度的顺序依次为D＞B＞A＞C。

(3)对于P20模具钢，在试验取值范围内，选取较小的行距和进给量，较高的铣削速度和较小铣削深度，可以得到较好的加工表面质量。

［1］Grzesik W.High speed machining［M］.Advanced Machining Processes of Metallic Materials.Elsevier，2008:213-226.

［2］王素玉，赵军.高速切削表面粗糙度理论研究综述［J］.机械工程师，2004(10):3-6.

［3］《正交试验法》编写组编.正交试验法［M］.北京:国防工业出版社，1976.

［4］刘晓志，陶华，李茂伟.钛合金TC18铣削表面粗糙度预测模型的研究［J］.组合机床自动化加工技术，2010(7):8-11.

［5］李之雁，胡传荣.试验设计与数据处理［M］.北京:化学工业出版社，2005.

Prediction Model of Surface Roughness on P20 Mold Steel by High Speed Milling

CHEN Jin-jiang，LONG Chao，WANG Chao
(College of Mechanical Engineering，Yanshan University，Qinhuangdao Hebei 066004，China)

To improve the machining quality of P20 mold steel，the main variables such as high-speed milling，the influence parameters of milling speed，feed per tooth，milling depth and line spacing on the surface roughness are analyzed based on orthogonal experiment.The surface roughness predictive model is established by multiple linear regression analysis.The results indicate that the model has reliability on surface roughness by variance analysis.

high-speed milling;the surface roughness;prediction model;P20 mold steel

TH161.14

A

1001-2265(2012)12-0060-03

2012-04-04

陈锦江(1962—)，男，河北雄县人，燕山大学副教授，博士，主要从事轴承设计制造、快速设计及高速加工等研究，(E-mail)chenjj@ysu.edu.cn。

(编辑 李秀敏)