以程海为例用支持向量机回归算法预测叶绿素a浓度

许云峰，马春子，霍守亮，席北斗，钱光人*

1.上海大学环境与化学工程学院，上海 200444

2.中国环境科学研究院，北京 100012

以程海为例用支持向量机回归算法预测叶绿素a浓度

许云峰1，马春子1，霍守亮2，席北斗2，钱光人1*

1.上海大学环境与化学工程学院，上海 200444

2.中国环境科学研究院，北京 100012

应用支持向量机回归(SVR)算法预测程海富营养化水体叶绿素 a(Chl-a)的浓度，用留一法交叉验证(LOOCV)优化SVR预测模型的参数，并根据平均相对误差(MRE)，讨论SVR预测模型的准确性。结果表明:用径向基核函数构建的SVR预测模型预测结果最优;SVR预测模型的预测值和实测值具有很好的一致性，相关系数为0.938，MRE为12.30%。SVR预测模型的建模结果优于人工神经网络(BP-ANN)预测模型，说明SVR算法能够准确预测 Chl-a浓度。

支持向量机回归(SVR);叶绿素a;程海;径向基核函数

水体富营养化已经成为我国大多数湖泊水质恶化的主要问题，其主要表现为溶解氧浓度降低、生物多样性减少、水体叶绿素a(Chl-a)浓度升高，爆发水华等［1-3］。氮磷等营养物的过量输入是导致水体富营养化的主要原因。因此，水体富营养化的早期预测很有必要［4］。

近几十年来，三维模型［5］、SALMO 确定性模型［6］等多种模型被用于水体富营养化的预测，其中，人工神经网络(BP-ANN)模型因其方法简单和预测能力相对较好，被广泛应用［7］。但是，BPANN模型在处理小样本和多变量数据时容易产生过拟合现象［8］，即可能产生很好的拟合效果却得不到好的预测结果。

支持向量机回归(SVR)算法［9-10］是以 Vapnik创立的统计学习理论为基础建立的数据处理新算法。该方法从严格的数学理论出发，论证和实现了在小样本情况下最大限度地提高预报的可靠性，实际应用取得了令人满意的研究成果。同时，该方法还能避免BP-ANN模型的过拟合现象，具有很好的泛化能力。目前，SVR算法已应用于化学合成［8］、材料优化［8］、浮游植物种类预测［11］和藻类生长评价［12］等许多领域。

笔者以程海为例，运用SVR算法预测富营养化水体的Chl-a浓度。先对SVR预测模型的参数进行优化，然后用SVR算法建立Chl-a浓度的预测模型，并与BP-ANN预测模型的结果进行比较。

1 数据与方法

1.1 程海数据分析

通过调查分析，确定程海的主要水质指标:Chl-a浓度，μg/L;总氮(TN)浓度，mg/L;总磷(TP)浓度，mg/L;水温(Tw)，℃;透明度(SD)，cm;电导率(γ)，μS/cm;溶解氧(DO)浓度，mg/L;化学需氧量(CODCr)，mg/L;高锰酸盐指数(CODMn)，mg/L。这些指标会对程海藻类的生长产生直接或间接的影响，进而影响水体中的 Chl-a 浓度［13-15］。程海的物理、化学指标数据来自1988—2008年云南省环境监测站的常规监测数据，以及笔者的现场调查。

由于程海缺少1988—2005年的Chl-a浓度监测数据，因此需采用SVR和BP-ANN分别建立定量预测模型进行预测。

以 Chl-a 浓度为目标变量;SD，DO 浓度，CODCr，CODMn，γ，Tw，TN 浓度和 TP浓度等变量为影响因素，以37个样本为训练集，建立了SVR和BPANN预测模型。

1.2 支持向量机回归

SVR通过引入不敏感函数(ε)进行回归分析，可以得到较好的回归分析结果。将实际问题通过非线性映照映射到高维特征空间，并在高维特征空间构造线性回归，从而取得在原始空间的非线性回归效果［16］。

设样本集为:(Y1，X1)，…，(Yi，Xi)，X ∈ Rn，Y∈R。回归函数用下列线性方程表示:

式中，Y为目标函数;Φi(X)为输入向量的非线性映射集;wi和B为系数。各值的大小由最小化正规化风险函数R(C)来确定。R(C)可表示为:

为了确保最优化问题有解，引入松弛变量ζi和，回归预测模型可表示为:

约束于

根据优化条件可以得到支持向量回归机的对偶问题:

在一定约束条件下

最后，得到支持向量机的回归估计公式［17-19］:

式中，K(Xi，Xj)为核函数，其值为特征空间Φ(X)中两个结果向量 Xi和 Xj的乘积，即 K(Xi，Xj)=Φ(Xi)Φ(Xj)。核函数的优势在于能在不知道Φ(X)具体变换形式的情况下，用低维空间数据输入计算高维特征空间中的点积［20］。在实际应用中，常用的核函数有线性核函数、多项式核函数、径向基核函数三种，具体形式如下。

线性核函数:

多项式核函数:

径向基核函数:

2 结果与讨论

2.1 SVR预测模型参数的选择

所有输入模型的数据都进行标准化预处理。由于数据样本较少，故采用留一法交叉验证(LOOCV)［8］选择SVR预测模型的参数。将n个样本分成两个不相关的子集，分别为训练集(n-1个样本)和预测集(1个样本)。n个样本轮留作为预测集，对另外n-1个样本建立的训练模型进行验证，得到预测值与实际值之间的差别。用平均相对误差(MRE)来评价模型预测能力的好坏:

式中，ei为第i个样本的实际值;pi为第i个样本的预测值;n为LOOCV的样本总数。

图1为C=10时，三种核函数的MRE随ε的变化;图2为ε=0.01时，三种核函数的MRE随C的变化。由图1和图2可见，用径向基核函数构建的SVR预测模型得到的平均相对误差最小。说明径向基核函数可以对程海的Chl-a浓度进行更好的定量预测。

图1 C=10不敏感函数(ε)对应的MREFig.1 MRE in LOOCV versus the ε with C=10

图2 ε=0.01平衡因子(C)对应的MREFig.2 MRE in LOOCV versus the C with ε=0.01

SVR预测模型预测能力的强弱与核函数的选择有很大的关系，不同核函数对MRE的影响很大。同时，参数ε和C也非常重要，其不仅权衡最大空白与最小训练误差，也会影响训练和预测结果，因此，参数ε和C应与核函数类型一起进行优化。通常情况下，ε和C值在建模前是不确定的，其值大小取决于数据的类型。ε值过大，算法在拟合数据过程中会出现压力不足现象;ε值过小，训练数据集将会出现过拟合现象。而C的变化与ε基本相反［8］。

用径向基核函数对程海的数据建立SVR预测模型，并采用网格法进行ε和C的参数优化。图3表示径向基核函数MRE随ε(步长为0.01)和C(C=1～10时步长为1;C=10～100，步长为10)的变化趋势。从图3可以看出，选用径向基核函数建立SVR预测模型对应的平均相对误差最低(C=10，ε =0.03，σ =1)。

图3 径向基核函数不同ε和C时对应的MREFig.3 MRE in LOOCV versus C and ε with RBF kernel function

2.2 SVR预测模型的建立

根据2.1节得到的最优核函数及最佳ε和C的组合，使用程海的水质指标(SD，DO浓度，CODCr，CODMn，γ，Tw，TN 浓度和 TP 浓度)建立了 Chl-a 浓度的最佳SVR预测模型。以37个样本点作为训练集对Chl-a浓度建立SVR预测模型，如图4所示。

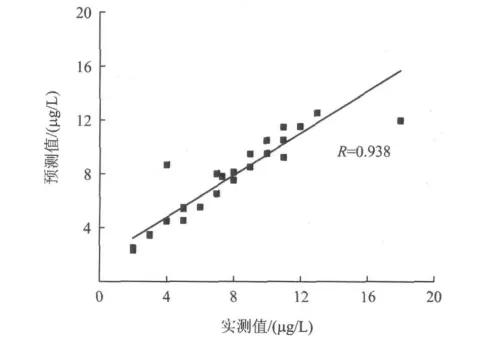
图4 Chl-a浓度SVR建模结果Fig.4 The result of SVR model of Chl-a concentration

Chl-a浓度最佳SVR预测模型的回归方程为:

式中，βi=表示支持向量的拉格朗日系数。根据式(13)可以得到Chl-a浓度的预测值，对预测值和实测值进行比较，相关系数为0.938。这表明SVR预测模型的预测值与实测值具有高度的一致性。

2.3 SVR预测模型与BP-ANN建模结果比较

为了评价SVR预测模型的预测和泛化能力，将其与BP-ANN预测模型进行比较。应用三层(输入层、隐含层和输出层)BP-ANN模型建模，BPANN预测模型经过参数优化，确定隐含层节点数为5。选择Sigmoid函数为转换函数，预测误差用MRE表示。图5为用BP-ANN建立的Chl-a浓度预测模型。

由图4和图5可知，SVR对Chl-a浓度的建模结果与实际结果十分吻合，实测值和预测值的相关系数为0.938，通过公式计算得到MRE为12.30%。BP-ANN预测模型实测值和预测值的相关系数为0.933，通过公式计算得到 MRE为25.72%，高于SVR预测模型。因此得出，SVR预测模型的建模结果明显好于BP-ANN预测模型，所以用SVR预测模型来预测程海的Chl-a浓度更加可靠。

图5 Chl-a浓度BP-ANN建模结果Fig.5 The result of BP-ANN model of Chl-a concentration

3 结论

(1)在参数优化过程中，在合适的ε和C下选择径向基核函数建立SVR预测模型得到的结果平均相对误差最小，说明径向基核函数更适合对程海的复杂富营养化问题进行预测。

(2)用SVR建模的相关性系数为0.938，说明模型的预测值与程海的实测值具有高度的一致性，表明，程海的Chl-a浓度可以用SVR预测模型来定量预测。

(3)SVR预测模型的建模结果明显好于BPANN预测模型，说明对于Chl-a浓度的预测，SVR算法具有更高的可靠性。

(4)根据建立的SVR预测模型，对收集的程海实测数据样本的Chl-a浓度进行定量预测，所预测的Chl-a浓度可以为多元统计方法推测程海营养物基准参照状态提供数据。

［1］PRETTY J N，MASON C F，NEDWELL D B，et al.Environmental costs of freshwater eutrophication in England and Wales［J］.Environ Sci Technol，2002，37(2):201-208.

［2］DODDS W K，BOUSKA W W，EITZMANN J L，etal.Eutrophication of US freshwaters:analysis of potential economic damages［J］.Environ Sci Technol，2008，43(1):12-19.

［3］XUE X，LANDIS A E.Eutrophication potentialoffood consumption patterns［J］.Environ Sci Technol，2010，44(16):6450-6456.

［4］KARUL C，SOYUPAK S，ILESIZ A F，et al.Case studies on the use of neural networks in eutrophication modeling［J］.Ecological Modelling，2000，134(2/3):145-152.

［5］MAO J，CHEN Q，CHEN Y.Three-dimensional eutrophication model and application to Taihu Lake，China［J］.J Environ Sci，2008，20(3):278-284.

［6］WALTER M，RECKNAGEL F，CARPENTER C，et al.Predicting eutrophication effects in the Burrinjuck Reservoir(Australia)by means of the deterministic model SALMO and the recurrent neural network model ANNA［J］.Ecological Modelling，2001，146(1/2/3):97-113.

［7］JIANG Y，XU Z，YIN H.Study on improved BP artificial neural networks in eutrophication assessment of China eastern lakes［J］.J Hydrodynamics:B，2006，18(3，Suppl):528-532.

［8］LIU X，LU W C，JIN S L，et al.Support vector regression applied to materials optimization of sialon ceramics［J］.Chemometrics Intelligent Laboratory Systems，2006，82(1/2):8-14.

［9］VAPNIK V N.A nature of statistical learning theory［M］.New York:Springer Verlag，1995.

［10］VAPNIK V N.Statistical learning theory［M］.USA:A Wiley-Interscience Publication，John Wiley and Sons Inc，1998.

［11］RIBEIRO R，TORGO L.A comparative study on predicting algae blooms in Douro River，Portugal［J］.Ecological Modelling，2008，212(1/2):86-91.

［12］YAN Q，WANG G.Prediction model of alga's growth based on support vector regression［C］//2009 International Conference on Environmental Science and Information Application Technology:2.Wuhan:ESIAT，2009:673-675.

［13］侯延鹏.营养元素及光照、温度对铜绿微囊藻生长、越冬及复苏的影响研究［D］.南昌:南昌大学，2008.

［14］王珂.不同环境条件下铜绿微囊藻和栅藻竞争能力的比较研究［D］.南京:河海大学，2006.

［15］蒙万轮.重庆郊区水库水体富营养化试验研究［D］.重庆:重庆大学，2005.

［16］YANG S，LU W，CHEN N，et al.Support vector regression based QSPR for the prediction of some physicochemical properties of alkyl benzenes［J］.J Molecular Structure:THEOCHEM，2005，719(1/2/3):119-127.

［17］GU T，LU W，BAO X，et al.Using support vector regression for the prediction of the band gap and melting point of binary and ternary compound semiconductors［J］.Solid State Sciences，2006，8(2):129-136.

［18］CHALIMOURDA A， SCHOLKOPF B， SMOLA A J.Experimentally optimal ν in support vector regression for different noise models and parameter settings［J］.Neural Networks，2004，17(1):127-141.

［19］RIAHI S，POURBASHEER E，GANJALI M R，et al.Support vector machine-based quantitative structure-activity relationship study of cholesteryl ester transfer protein inhibitors［J］.Chemical Biology Drug Design，2009，73(5):558-571.

［20］王宏宇，糜仲春，梁晓艳，等.一种基于支持向量机回归的推荐算法［J］.中国科学院研究生院学报，2007，24(6):742-748.

Using Support Vector Regression Algorithm to Predict Chlorophyll-a Concentrations with Chenghai Lake for Example

XU Yun-feng1，MA Chun-zi1，HUO Shou-liang2，XI Bei-dou2，QIAN Guang-ren1
1.School of Environmental and Chemical Engineering，Shanghai University，Shanghai 200444，China
2.Chinese Research Academy of Environmental Sciences，Beijing 100012，China

The support vector regression(SVR)algorithm was used to predict the concentration of chlorophyll-a(Chl-a)of eutrophication water in Chenghai Lake，and the leave-one-out cross-validation(LOOCV)method was used to optimize the model parameters.Then the prediction accuracy of SVR model was discussed on the basis of the mean relative error(MRE).The results demonstrated that the SVR model built by radial basis kernel function(RBF)had the optimal predictive ability.The predicted values of SVR were in good consistency with the measured values of experiment.The correlation coefficient(R)and MRE of SVR model could reach 0.938 and 12.30%，respectively.It was found that the modeling results of SVR were better than that of back propagation artificial neural networks(BP-ANN)，suggesting that SVR was a valuable tool for the prediction of Chl-a.

support vector regression(SVR);chlorophyll-a;Chenghai Lake;radial basis kernel function

X524

A

10.3969/j.issn.1674-991X.2012.03.031

1674-991X(2012)03-0207-05

2011-12-21

国家水体污染控制与治理科技重大专项(2009ZX07106-001)

许云峰(1971—)，女，副教授，博士，主要从事水污染控制工程研究，yfxu@shu.edu.cn

*责任作者:钱光人(1960—)，男，教授，博士，主要从事环境污染控制材料及废弃物资源化的研究，grqian@shu.edu.cn