优化课堂结构提高数学课堂效率

2012-09-08 03:48秦晓丽

中国教育技术装备 2012年1期

秦晓丽

减轻学生负担，提高课堂教学的有效性是新课改的重要目标，而实现这个目标的前提是优化课堂结构，提高课堂效率，使教学效果最大化。而数学课堂结构模式是开放性的，结合教学实践，笔者认为新课改下有效的数学课堂结构，应包括情境创设、探索活动、精讲例题、巩固练习、课堂小结5个部分。

1 情境创设

有人说开始3分钟就能基本看到一节课的效果，说明情境创设在实现有效教学过程中的重要性。所谓教学情境是一种激发学生问题意识为价值取向的刺激性的数据材料和背景信息，是从事教学活动的环境，产生教学行为的条件。好的情境能激发起学生的疑问，从而产生兴趣，进而调动学生学习新知识的积极性和自觉性。如何创设高质量的数学问题情境？首先要关注创设的问题情境能否引起更多学生的兴趣，引起更多的深入思考；其次要关注问题的“障碍性”是否符合学生的认知水平，是否符合学生的最近发展区。

例如，在讲“确定圆的条件”这节课时，教师先给出这样的教学情境：小芳不小心打碎同学心爱的圆形镜子，为了不让同学失望，她拿了其中的一块碎片（图1），到玻璃店准备划新镜子。接着教师提出问题：画玻璃的师傅能否划出一模一样的镜子？确定圆需要哪些条件？（用几何画板演示一动圆。）经过一点可以作无数条直线，经过两点确定一条直线，那么经过几点可以确定一个圆？这样的问题情境贴近学生的实际，能真正引起学生的共鸣，激发学生学习的兴趣。由直线到曲线，由三角形到圆，符合学生的最近发展区。

图1

2 探索活动

学生是学习的主体，教师是学生学习的组织者、引导者和合作者。因此，教师在数学课堂教学中应重视知识的发生和发展，给学生留有充分的时间和空间进行探索。在设计数学教学活动过程中，教师要提供可供学生进行有效活动的问题串，随时观察学生在思考什么，思维上有无障碍，如何引导。数学是一门比较抽象的学科，很多数学概念、数学规律都是借用符号来表达。因此，教师在设计探索活动时必须考虑通过多种途径，采用多种不同的方法分析、讲解，帮助学生透彻地理解概念的内涵和外延。

如某位教师在教学“有理数的加法”时，设计问题串，供学生探索。

1）学生根据生活经验讨论诸如“一个同学在一条东西的跑道上，先向东走了20米，又向东走了30米，能否确定他现在的位置位于出发点的哪个方向？与原来的位置相距多少米”等有关在出发点的东边与西边的4个问题。

2）就其中一个问题讲解怎样用正负数表示，在出发点的东边还是西边，怎样将行走过程与结果数学化。如先向东走20 m，再向东30 m，可以记作(+20)+(+30)=+50。再提出问题：你能把其他3个问题中的行走过程与结果用等式表示出来吗？

3）在讨论4个等式含义的基础上，提问：你能用上面的方法表示出“先向东走10 m，再向西走20 m”“先向西走30 m，再向东走100 m”行走过程与结果的式子吗？学生再次借助于生活经验，得出这几个问题的结论。

4）让学生汇总刚才得到的等式并用表格记录下来，在表格中还出现一些新的等式，要求学生填空，如(-70)+(+30)=，在学生填上答案后，还要用语言叙述这些等式的含义。

5）由学生讨论问题：两个有理数相加，和的符号如何确定？和的绝对值如何确定？

有理数的加法法则是一个规定，如何让学生从生活情镜中感受它的合理性，如何引导学生一步一步理解它的内涵并概括它，这正是教师创设的一串问题串的目的。从这个设计中可以看出，教师把这个探索活动问题化，通过这些问题串，学生解决一个个问题，逐步把学生从生活实际中的行走位置引导到教学内容有理数的加法法则，在学生观察、探索、讨论后，对加法法则的归纳和接受就水到渠成。

3 精讲例题

在课堂教学中，例题能承上启下，能够加深对概念、公式、定理的理解，还能启迪学生的思维，培养学生的能力，发展学生的智力。因此，教师要精选例题，按照例题的难度、结构特征、思维方法等进行全面剖析，不片面追求例题的数量，而要重视例题的质量。笔者认为，例题的选取应以教材中的例题为主，教材中的例题是经过众多的专家严格筛选出来的，具有很强的科学性、典型性、示范性和可操作性。在使用时，教师可根据学生的实际情况，向学生提供适当的帮助或进行一定的拓展延伸。通过例题的讲解，让学生学会规范的说理、书写等。

4 巩固练习

巩固练习可分为基础训练和拓展延伸两个部分。基础训练应以人人能够掌握的目标描述的学习内容入手，体现层次分明的递进特点，防止机械的重复。基础训练以学生掌握基础知识、基本技能为主，以培养能力为辅，通过基础训练，让学生将自主构建的新知进行内化。而拓展延伸是针对学有余力的学生设计的，目的是允许学生认知上的差异，满足多样化的学习需求，让每一位学生都能按需学习。正如新课标所要求的：不同的人在数学上获得不同的发展。拓展延伸在选题时要切合本节课内容，让学生跳一跳能够着果子。如某位教师在教师“勾股定理”时，给出问题：如图2，两个边长不同的正方形连在一起，请你剪两刀，再把所得的图形拼成一个正方形。

通过本节课的学习，学生能够解决这个问题，感觉成功的喜悦。本题的实质是陈杰证明勾股定理的方法，为下节课勾股定理的证明做了铺垫。

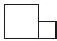
图2

5 课堂小结

课堂小结是整个课堂教学过程中不可忽视的一部分，学生动脑、动手，发自内心的课堂小结，既能巩固学生的记忆，又能活跃课堂气氛，还能激发学生进一步探究的欲望，起到画龙点睛的作用。而许多数学教师在常态课中往往因为时间关系而草草收场或代为包办，唯恐学生讲的不清楚，归纳不全面，分析不透彻，留给学生的只有机械的听、记、写，忽视学生的主体作用。结果，学生对知识的掌握往往不系统。

一个好的课堂小结，必须建立在民主和谐的教学氛围上，留有充足的时间让学生“议”，放开手脚让学生“说”。教师要紧扣教学重、难点，引导学生对学习过程、方法、结果及体验进行反思，抛出有价值的问题，引发学生进一步的思考，为下一节课的教学内容作一个铺垫。