基于稀疏存储Elman神经网络的直线伺服控制

左健民 潘 超 汪木兰

1.江苏大学，镇江，212013 2.江苏技术师范学院，常州，213001

3.上海铁路局，上海，200071 4.南京工程学院，南京，211167

0 引言

电动机直接带动负载实现“零传动”是理想高效的传递方式，永磁直线同步电动机（permanent magnet linear synchronous motor，PMLSM）取消了电机到负载之间的机械传动环节，由电动机直接驱动工作部件运动［1］，力能指标高，体积小，重量轻，具有响应速度快、灵敏度高、随动性好、容易获得高速度和高加速度的优点，是高性能数控机床进给系统的理想部件。但从控制角度分析，直线交流伺服系统是一个非线性、强耦合和时变性的复杂系统；从数控机床的工作状态分析，进给系统又是重复运动的非线性动态系统，工作过程中受到切削力变化、负载变化等各种外部扰动的影响。因此要想实现对数控机床直线进给伺服系统的控制，既要对控制对象的结构和参数有清楚的认识，又要考虑其存在的模型摄动、端部效应及负载扰动等不确定因素［2］。

神经网络具有自组织、自学习和分布式存储等特点，能以任意精度逼近任意连续复杂的非线性函数，具有很好的鲁棒性。其中，动态递归神经网络通过存储内部状态，具有映射动态特性的功能和适应时变特性的能力，适合于高性能数控机床直线伺服系统的控制［3－4］。

本文提出具有稀疏存储功能的改进Elman神经网络，利用前一次或前几次的控制信息来提高进给系统的动态性能［5］，并对网络存储的历史控制信息进行稀疏存储、选择利用，以提高网络的收敛速度和泛化能力，该网络具有局部逼近的快速性和递归神经网络的动态性能，在保证动态性能的同时减小了伺服控制器的计算量和存储空间，满足了直线伺服系统实时性的要求。

1 稀疏存储Elman神经网络设计

1.1 标准Elman神经网络

Elman网络是一种典型的动态递归神经网络，因其“部分递归、全局前馈”的结构兼备多层前馈神经网络的优点，在直线伺服系统的控制中得到良好的应用［6－7］。

标准Elman神经网络结构如图1所示。它具有输入层、隐层、链接层和输出层四层神经元［8］。链接层主要用来记忆网络的“内部状态”，通过动态递归过程反映出所有历史信息对当前系统的影响，直接反应系统动态过程，具有适应时变特性的能力。

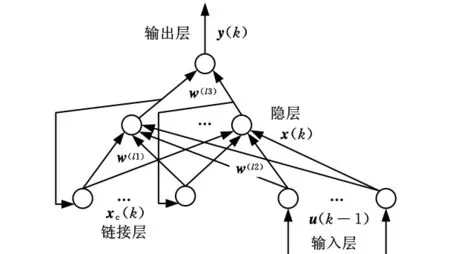
图1 标准Elman神经网络结构图

设网络输入为u（k－1），输出为y（k），隐层输出为x（k），链接层的输出为xc（k），则该神经网络的数学模型为

设网络的输入层、隐层和链接层、输出层的节点数分别为q、n、n和m，则连接权w（l1）为n×n矩阵，w（l2）为n×q矩阵，w（l3）为m×n矩阵，f（x）取sigmoid函数，即

1.2 稀疏存储Elman网络

Elman网络作为一个局部循环网络，隐层和链接层需要较多的神经元和较长的训练时间。Elman神经网络链接层存储的信息反映了全部的历史信息，未对存储的信息进行筛选利用，一般仅能实现对给定函数的逼近，因此网络泛化能力不足。

为提高网络的泛化能力和快速性，结合小脑对外部信号具有不假思索迅速联想的特点，在标准Elman网络的隐层和链接层之间引入具有迅速联想功能的查表方式，网络结构如图2所示。以隐层信息作为激励信息，利用小脑工作原理的迅速联想功能找寻到和输入状态相关的历史控制信息并反馈给隐层神经元，经过输出计算提高控制器的动态响应性能。在此过程中只有少量的连接权值需要进行调整，是一种稀疏连接方式，相比全局逼近网络具有学习速度快的优点，更适合于复杂动态环境下非线性实时控制［9－10］。

图2 稀疏存储Elman神经网络结构图

隐层和链接层之间的稀疏连接主要通过概念映射和物理映射两个阶段来实现。

（1）概念映射。概念映射是从隐层神经元到虚拟存储器Ac的映射，映射原则为：在输入空间相近的两个点，在Ac中有部分的重叠单元被激励，距离越近，重叠越多，距离越远，重叠越少，这种映射称为局部泛化，泛化能力提高了神经网络对未知模式的逼近或分类能力。图2中，α＝（α1，α2，…，αm）T是m维相联空间Ac中的向量，αi只取1或0两个值。对于确定的x（k），只有其中少数元素为1，大部分元素为0，其中值为1的元素的个数c为泛化参数。

（2）物理映射。物理映射是由虚拟存储器Ac中的c个单元，用稀疏编码技术映射到实际物理存储器Ap的c个单元，c个单元存放着相应权值。

稀疏存储是一种对学习数据出现的次序不敏感的非线性逼近器，因此可以把n维输入的概念映射降阶为n个一维输入，同时把c×n权值矩阵w（l1）降阶为n个c×1稀疏连接矩阵，则具有稀疏存储功能的Elman神经网络的数学模型为

1.3 权值调整

稀疏存储Elman神经网络的学习过程根据网络期望输出与实际输出的误差em来更新各层权值。学习算法采用动态BP算法，对w（l3）和w（l2）有：

稀疏存储Elman网络中，隐层的每个神经元都对链接层中的c个权值进行如下的调整：

式中，η1、η2、η3分别为链接层、输入层和输出层的学习速率；β为动量因子。

2 稀疏存储Elman神经网络直线伺服系统设计

2.1 矢量控制PMLSM直线伺服系统设计

直线伺服系统的任务是控制和调节直线电动机的位置、速度和推力，采用矢量控制，令电流Id＝0，电磁推力就随着电流Iq的变化而变化，在控制系统中只要控制Iq大小就能控制推力和速度。对于PMLSM，次级磁通位置与次级的机械位置相同，这样就可以通过光栅尺等检测设备得到次级的机械位置和磁通位置。图3为PMLSM的矢量控制原理图，速度环采用本文所设计的稀疏存储Elman神经网络进行控制。

图3 PMLSM矢量控制原理框图

2.2 稀疏存储Elman神经网络速度控制器设计

在本项目设计的直线伺服控制系统中，使用科尔摩根公司型号为IC22－050A2P1的永磁直线同步电动机，其峰值推力为1250N，额定推力为548N，推力系数为63.0N／A，电气时间常数为10.1ms，电阻为1.3Ω，电感为0.0134H，反电势常数为51.4V／（m·s－1），动子质量为6.9kg，极距τ＝0.032m，根据PMLSM数学模型可以推导其传递函数为

稀疏存储Elman神经网络速度控制器的输入为u（k－1）＝（e（k），e（k－1），e（k－2）），其中e（k）、e（k－1）、e（k－2）分别为k、k－1、k－2时刻的速度偏差。

对隐层神经元进行概念映射方法如下：隐层空间x在区间［Xmin，Xmax］上分成N＋2C个量化间隔，即

实际映射的方法为

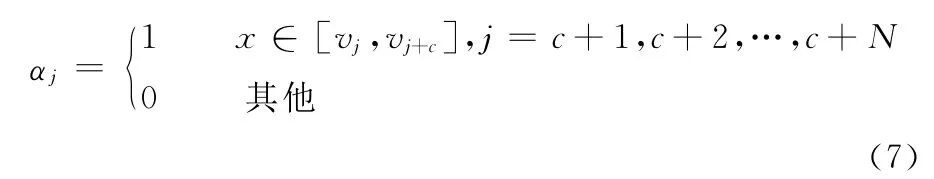
控制的最终目的是使控制对象更好地跟踪给定信号，因此以速度偏差值作为网络的辨识误差来训练网络，使网络调整向减小误差的方向进行。因此取辨识指标为

稀疏存储Elman神经网络速度控制器的具体参数为：输入层节点数为3，隐层节点数为10，链接层物理存储空间节点数为100，输出层节点数为1，Xmin＝0，Xmax＝1，N ＝100，c＝5，η1＝η2＝η3＝0.02，β＝0.4。

3 仿真研究

根据上述分析，在MATLAB软件中建立了直线伺服系统仿真模型，首先验证了速度控制器的动态跟踪能力，图4和图5所示分别为跟踪正弦速度指令和梯形重复运动速度指令的仿真结果。从图中可以看出，稀疏存储神经网络速度控制器能使直线进给系统具有良好的跟踪能力。图6和图7分别为在直线电动机平稳运行中受到正弦干扰（FL＝（50sin5t＋50）N）和突加外力（FL＝150N）时的速度响应曲线，从结果可以看出，改进后的Elman网络速度控制器具有良好的抗干扰能力，特别是对具有周期特性的正弦干扰具有明显的抑制效果。

图4 正弦速度信号跟踪曲线

图5 重复运动速度跟踪曲线

图6 正弦力干扰下的速度跟踪曲线

图7 突加负载情况下的速度跟踪曲线

4 结束语

为满足数控机床直线进给系统高速高精的要求，本文在Elman神经网络隐层与链接层之间引入迅速联想的查表方式，对网络控制信息进行分类存储，提高了网络的学习速度和泛化能力，使改进后的稀疏存储Elman神经网络具有局部逼近的快速性和反馈神经网络的动态性能，同时使控制器计算量和存储空间减少，实现计算的快速性。在数控机床直线伺服系统上的仿真结果验证了稀疏存储Elman神经网络直线伺服控制器有良好的跟踪性能和抗干扰能力。

［1]王国彪，赖一楠，范大鹏，等.新型精密传动机构设计与制造综述［J］.中国机械工程，2010，21（16）：1891－1897.

［2]郭庆鼎，赵希梅.数控机床直线伺服驱动控制的若干问题与展望［J］.沈阳工业大学学报，2006，28（3）：273－277.

［3]Lin Faa－Jeng，Wai Rong－Jong，Chou Wen－Der，et al.Adaptive Backstepping Control Using Recurrent Neural Network for Linear Induction Motor Drive［J］.IEEE Transactions on Industrial Electronics，2002，49（1）：134－146.

［4]Yildirim S.Design of Adaptive Robot Control System Using Recurrent Neural Network［J］.Journal of Intelligent and Robotic Systems，2005，44（3）：247－261.

［5]侯忠生，许建新.数据驱动控制理论及方法的回顾和展望［J］.自动化学报，2009，35（6）：650－667.

［6]Zuo Jianmin，Pan Chao，Wang Mulan，et al.Elman Dynamic Neural Network Control for Direct－Drive Feed System in Advanced CNC Machine Tools［C］／／2010International Conference on Computer，Mechatronics，Control and Electronic Engineering.Changchun，2010：307－310.

［7]潘超，左健民，汪木兰.基于前馈及反馈补偿的高性能直线伺服系统［J］.系统仿真学报，2010，22（12）：3025－3029.

［8]迟军，陈廉清，杨超珍.基于小波包分析和Elman网络切削表面粗糙度预测方法［J］.中国机械工程，2010，21（7）：822－826.

［9]Peng Ya－Fu，Lin Chih－Min.Adaptive Recurrent Cerebellar Model Articulation Controller for Linear Ultrasonic Motor with Optimal Learning Rates［J］.Neurocomputing，2007，70（16／18）：2626－2637.

［10]汪木兰.神经网络硬化实现的共性技术在电力传动中应用研究［D］.合肥：合肥工业大学，2010.