调和映照的Landau定理

李东征，陈行堤

（华侨大学数学科学学院，福建泉州362021）

调和映照的Landau定理

李东征，陈行堤

（华侨大学数学科学学院，福建泉州362021）

研究调和映照的Landau定理和单叶性半径估计问题，结合有界单叶函数的Koebe定理和调和映照的Schwarz引理，得到Landau常数的渐进精确表示，改进了陈怀惠等近期的研究结果.

调和映照；Landau定理；Bloch常数；单叶函数

1 预备知识

单连通区域Ω⊂C内的C2复值函数f（z）被称为调和的，当且仅当它满足由文献［1］可知，存在Ω上两个解析函数h（z）与g（z），使得f＝h＋g¯.

记Λf（z）＝max｜fz（z）＋e－2iθfz¯（z）｜＝｜fz（z）｜＋｜fz¯（z）｜＝｜h′｜＋｜g′｜和λf（z）＝min｜fz（z）＋

0≤θ≤2π0≤θ≤2πe－2iθfz¯（z）｜＝｜｜fz（z）｜－｜fz¯（z）｜｜＝｜｜h′｜｜g′｜｜.根据Schwarz引理［2］，如果单位圆盘D＝｛z｜｜z｜＜1｝上的解析函数f（z）满足f（0）＝0，｜f（z）｜＜1，则有｜f′（0）｜≤1，且等号成立当且仅当f（z）＝eiαz，其中α为实常数.即如果｜f′（0）｜＝1，则f（z）在单位圆盘上都单叶且其单叶像圆盘半径为1.Landau［3］对｜f′（0）｜＝α，0＜α＜1的情形进行了研究，得到如下定理.

定理A［3］若f（z）为单位圆盘D上的解析函数，满足f（0）＝0，｜f（z）｜＜1，z∈D，｜f′（0）｜＝α＞0，则f（z）在圆盘Dr0上单叶，且f（Dr0）包含一个圆盘

文献［1，4－6］在有界像域和有界偏导数的两种规范条件下，展开了Landau定理在调和映照类中的推广研究；而在其他类中的推广研究也有不少成果［7－11］.

定理B［4］如果f（z）为单位圆盘D上的保向调和映照，且满足fz（0）＝α＞0，f（0）＝0，f¯z（0）＝0，｜f（z）｜＜1，z∈D，那么f（z）在某一包含原点的区域上单叶，其像区域包含一个以原点为圆心，R0为半径的圆盘.其中

在定理B中，未给出f（z）的单叶圆盘半径的估计.针对调和映照的单叶圆盘和单叶像圆盘的半径估计的两个问题，借助有界单叶函数的Koebe定理和调和映照的Schwarz引理［12－13］，可得到

定理1 如果D上的保向调和映照f（z）满足f（0）＝0，fz（0）＝α＞0，g（z）＝bmzm＋bm＋1zm＋1＋…（bm≠0，m≥2），｜f（z）｜＜1，则f（z）在圆盘Dr上单叶，且f（z）的单叶像区域包含一个以原点为中心，R1为半径的圆盘，R1＝（1－r0m－1）R″.

当2≤m≤3时，有

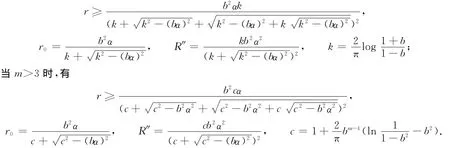
其中：b为小于1的正常数.

将定理1中的条件｜f（z）｜＜1换为其解析部分h（z），满足｜h（z）｜＜1，得到

定理2 若D上保向有界调和映照f（z）满足f（0）＝0，fz（0）＝α＞0，g（z）＝bmzm＋bm＋1zm＋1＋…（m≥2），｜h（z）｜＜1，则f（z）存在单叶圆盘Dr，且f（z）的单叶像区域包含DR.其中：r≥

要实现掘进机定向掘进，需要实时修正掘进机机身位姿，即需要建立掘进机机身空间位姿计算模型。假设巷道理想测量坐标系为OcXcYcZc，OcXc轴与巷道设计中线重合，指向巷道断面，OcZc轴指向巷道顶板，巷道底板平面由XcOcYc平面构成。掘进机机身坐标系位姿变化时，机身坐标系O0X0Y0Z0由测量坐标系OcXcYcZc经过3个旋转和1个平移变换得到。设掘进机的机身航向角为δ、机身俯仰角为φ和机身横滚角为γ，机身沿着X、Y和Z方向平移分别为PX、PY和PZ，则掘进机相对于测量坐标系的机身位姿T计算模型见式(4)。

近年来，对于局部单叶调和映照的单叶性问题（比如Landau定理、Bloch常数）的研究已有很多.在h（z）为单叶的条件下，对于f（z）的单叶性问题也开始被研究［14－15］.本文给出了一个在h（z）为单叶的条件下，f（z）的单叶圆盘及像区域单叶圆盘的半径估计.

定理3中的估计R渐近精确于经典Koebe定理的结果.

2 引理及其证明

引理A［7］设f（z）为单位圆盘到自身的调和映照，则sup（1－｜z｜2）（｜h′（z）｜＋｜g′（z）｜）≤.

z∈D

引理B［16］设f（z）∈S且｜f（z）｜＜M，z∈D，则有dist

文献［11］中估计了f（z）的解析部分为z时的单叶半径，得到

引理C［11］设f（z）＝z＋g（z），g（z）＝bmzm＋bm＋1zm＋1＋…，（bm≠0，m≥2）.f为Dr＝｛z∶｜z｜≤r｝上的K－拟正则调和映照，则f在Dr上单叶，且f（Dr）包含一个半径为Rm的单叶圆盘，Rm＝r（1－

引理1 若f为单位圆盘D上的保向调和映照且满足f（0）＝0，fz（0）＝α＞0，g（z）＝bmzm＋bm＋1× zm＋1＋…（bm≠0，m∈N，m≥2），｜f（z）｜＜1，则｜z｜≤b＜1，其中b是正常数.

当2≤m≤3时，有

当m＞3时，有

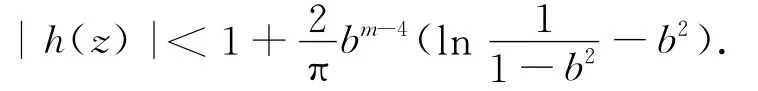
证明 记fz（z）的所有零点的集合为E，则在D＼E上，函数μ（z）＝f¯z／fz为全纯函数.由于f为D上的保向调和映照，知｜μ（z）｜≤1，故E是可去的，且μ（0）＝0.由Schwarz引理有｜μ（z）｜＜｜z｜m－1，即｜f¯z｜≤｜z｜m－1｜fz｜.

对于｜z｜≤b＜1，当2≤m≤3时，由引理A有

3 主要结果的证明

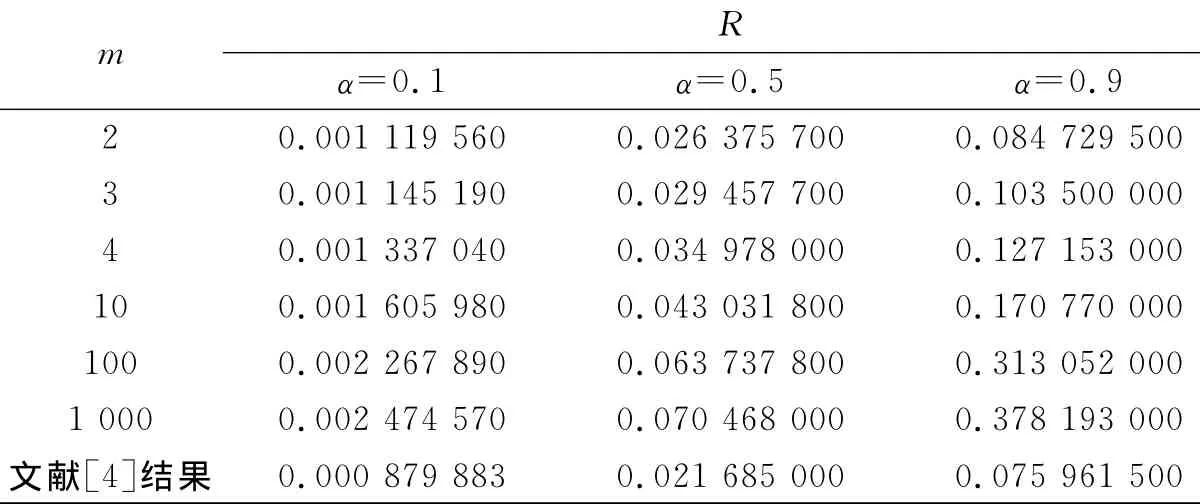
表1 圆盘半径R的比较Tab.1 Camparison of the disc radius R

注3 此定理给出调和映照具体的单叶区域Dr，是文献［4］没有指出的.

f（z）单叶像圆盘半径R与文献［4］比较，如表1所示.表1中：对于给定的α与m，关于b取极值，得到R的极大值.

注4 当m＝2，b＝1／2时，便与文献［4］中的R值是一样的.由此可知本定理的结果包含文献［4］的结果.

参考文献：

［1］ CHEN Huai－hui，GAUTHIER P M，HENGARTNER W.Bloch constants for planar harmonic mappings［J］.Proc Amer Math Soc，2000，128（11）：3231－3240.

［2］ AHLFORS L V.复分析［M］.北京：机械工业出版社，2005.

［3］ LANDAU E.Der picard－schottysche satz und die blochsche konstanten［M］.Berlin：Sitzungsber Press Akad Wiss，1926：467－474.

［4］ CHEN Huai－hui，GAUTHIER P M.The Landau theorem and Bloch theorem for planar harmonic and pluriharmonic mappings［J］.Proc Amer Math Soc，2011，139（2）：583－595.

［5］ GRIGORYAN A.Landau and Bloch theorems for harmonic mappings［J］.Complex Variable Theory Appl，2006，51（1）：81－87.

［6］ HUANG Xing－zhong.Estimates on Bloch constants for planar harmonic mappings［J］.J Math Anal Appl，2008，337（2）：880－887.

［7］ COLONNA F.The Bloch constant of bounded harmonic mappings［J］.Indiana Univ Math J，1989，38：829－840.

［8］ DORFF M，NOWAK M.Landau′s theorem for planar harmonic mappings［J］.Comput Meth Funct Theory，2004，4：151－158.

［9］ LIU Ming－sheng.Landau′s theorems for biharmonic mappings［J］.Complex Variables and Elliptic Equations，2008，53（9）：843－855.

［10］ LIU Ming Sheng.Landau′s theorem for planar harmonic mappings［J］.Computers and Mathematics with Applications，2009，57（7）：1142－1146.

［11］ 李东征，陈行堤.调和映照的Bloch常数［J］.华侨大学学报：自然科学版，2012，33（1）：103－106.

［12］ DUREN P.Harmonic mappings in the plane［M］.Cambridge：Cambridge Univ Press，2004.

［13］ 李忠.复分析导引［M］.北京：北京大学出版社，2004.

［14］ CHUAQUI M.HERNANDEZ R.Univalent harmonic mappings and linearly connected domains［J］.J Math Anal Appl，2007，332（2）：1189－1194.

［15］ 黄心中.具有线性连结像域的局部单叶调和映照［J］.数学年刊，2010，31A（5）：625－630.

［16］ PICK G.Über die konforme Abbildung eines Kreises auf ein schlichtes und zugleich beschränktes Gebiet［J］.S－B Kaiserl Akad Wiss Wien Math Natur Kl AbtⅡa，1917，126：247－263.

Landau Theorem for Planar Harmonic Mappings

LI Dong－zheng，CHEN Xing－di
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

In this paper，we study Landau theorem and the univalence radius for harmonic mappings in the plane.Combining Koebe theorem of bounded univalent functions and Schwarz lemma of harmonic mappings，we obtain an asymptotically sharp estimate of Landau constant for a harmonic mapping.Our results improve the ones recently gotten by H.H.Chen and P.M.Gauthier.

Harmonic mapping；Landau theorem；Bloch constant；univalent function

O 174.55

A

（责任编辑：陈志贤 英文审校：张金顺，黄心中）

1000－5013（2012）05－0584－06

2011－10－22

陈行堤（1976－），男，副教授，主要从事函数论的研究.E－mail：chxtt＠hqu.edu.cn.

国家自然科学基金资助项目（11101165）；福建省自然科学基金资助项目（2011J01011）；中央高校基本科研业务费专项基金资助项目，华侨大学基本科研专项基金资助项目（JB－ZR1136）