单位圆上调和映照的单叶半径

朱剑峰，王朝祥，黄心中

（华侨大学数学科学学院，福建泉州362021）

单位圆上调和映照的单叶半径

设f（z）＝h（z）＋为定义在单位圆盘U上的调和映照，满足条件证明当0＜p≤1时，f（z）在圆盘｜z｜＜r0＝1／（21－p）内单叶；当1＜p≤2时，f（z）在圆盘｜z｜＜R0＝1／（22－p）内为凸像函数.所得结果推广了M.Jahangiri等和M.Öztürk等的结论.

调和映照；单叶半径；星像函数；凸像函数

1 预备知识

h（z）和g（z）为D上的解析函数，称h（z）为f（z）的解析部分，g（z）为f（z）的共轭解析部分.由文献［1］可知：f（z）为D上的局部单叶保向映照的充要条件是｜h′（z）｜＞｜g′（z）｜，对于任意的z∈D.

记U＝｛z∶｜z｜＜1｝为单位圆盘，如果式（1）中的f（z）满足f（0）＝fz（0）－1＝0，则有

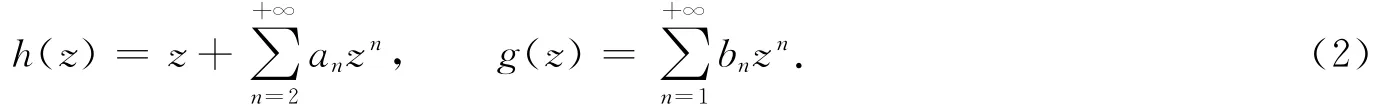
设f（z）＝u（x，y）＋i v（x，y）为定义在区域D上的连续函数，如果u（x，y），v（x，y）皆为实调和函数，则称f（z）为D上的复调和函数.又若D为单连通区域，则f（z）可写成

定义SH类函数为一族定义在单位圆盘U上的单叶保向调和映照且满足条件（2）.对于任意的f∈SH，若其像域f（U）为星像，则称f（z）为星像调和函数，记为f∈S＊H.类似地若其像域f（U）为凸像，则称f（z）为凸像调和函数，记为f∈KH.关于星像调和与凸像调和函数的特征，有如下充要条件［2］，即

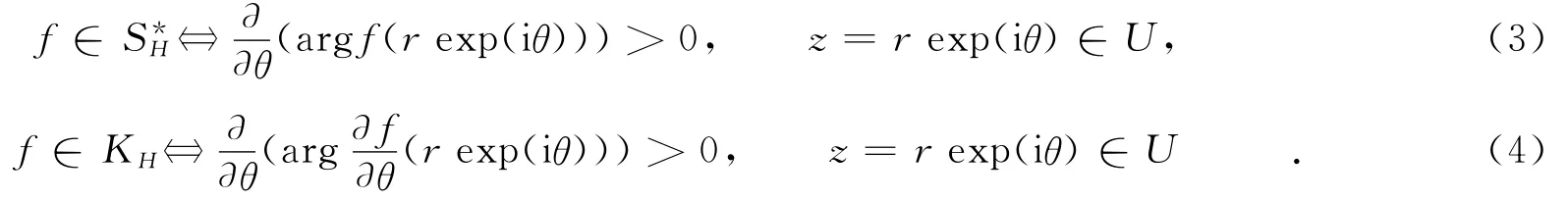
M.Jahangiri等［3－4］利用系数不等式证明了下列的定理.

定理A 设f＝h＋¯g为定义在单位圆盘U上的调和映照，其中h和g的定义如式（2），满足

则f（z）为U上的单叶、保向近于凸映照.式（5）的上限是精确的，因为对于任意的δ＞0，f（z）＝z＋内已不在单叶.进一步地，若有则f∈KH为U上的凸像函数.这里的上限同样是精确的，因为函数f（z）＝z＋，δ＞0表明式（6）的上界已无法再改进.

M.Öztürk等［5］进一步研究了上述问题.设f＝h＋g¯为单位圆盘U上的调和函数，其中h，g由式（2）定义，若其系数满足

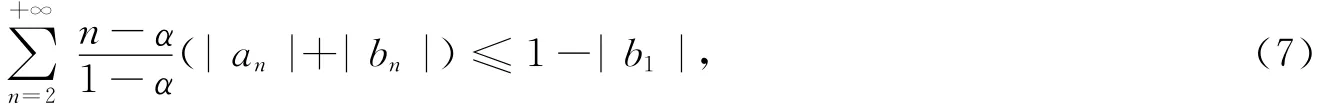
则f（z）为凸像函数.

2 主要结论及其证明

定理1 设f＝h＋¯g为定义在单位圆盘U上的调和映照，h和g如式（2）定义，对于任意的0＜p≤1，若f（z）满足

［1］ LEWY H.On the non－vanishing of the Jocobian in certain one－to－one mappings［J］.Bull Am Math Soc，1936，42（10）：689－692.

［2］ AHUJA P.Planar harmonic univalent and related mappings［J］.Journal of Inequalitities in Pure and Applied Mathematics，2005，6（4）：1－18.

［3］ JAHANGIRI M，SILVERMAN H.Harmonic close－to－convex mappings［J］.Journal of Applied Mathematics and Stochastic Analysis，2002，15（1）：23－28.

［4］ JAHANGIRI M，SILVERMAN H.Meromorphic univalent harmonic functions with negative coefficients［J］.Bull Korean Math Soc，1999，36（4）：763－770.

［5］ ÖZTÜRK M，YALCIN S.On univalent harmonic functions［J］.Journal of Inequalities in Pure and Applies Mathematics，2002，3（4）：1－8.

［6］ WIDOMAKI J，GREGORCZYK M.Harmonic mappings in the exterior of the unit disk［J］.Annales UMCS，Mathematica，2010，64（1）：63－73.

Univalent Radius of Harmonic Mapping in the Unit Disk

ZHU Jian－feng，WANG Chao－xiang，HUANG Xin－zhong
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

（｜an｜＋｜bn｜）≤1－｜b1｜.In this paper we prove that：if 0＜p≤1，then f（z）is univalent in the diskif 1＜p≤2，then f（z）is convex in the disk｜z｜＜R＝.These improve the corresponding results made by M.Jahan－0giri and M.Öztürk.

harmonic mapping；univalent radius；starlike mapping；convexity mapping

1000－5013（2012）05－0581－03

朱剑峰，王朝祥，黄心中

（华侨大学数学科学学院，福建泉州362021）

O 174.2

A

（责任编辑：黄晓楠 英文审校：黄心中）

2011－10－12

朱剑峰（1980－），男，讲师，主要从事函数论的研究.E－mail：flandy＠hqu.edu.cn.

国家自然科学基金资助项目（11101165）；国务院侨办科研基金资助项目（10QZR22）