一种改进的一维搜索指数优化算法

张志彬，金福江，汤仪平

（1.华侨大学信息科学与工程学院，福建厦门361021；2.华侨大学机电及自动化学院，福建厦门361021；3.福建凤竹纺织科技股份有限公司，福建泉州362200）

一种改进的一维搜索指数优化算法

张志彬1，金福江1，汤仪平2，3

（1.华侨大学信息科学与工程学院，福建厦门361021；2.华侨大学机电及自动化学院，福建厦门361021；3.福建凤竹纺织科技股份有限公司，福建泉州362200）

在分析黄金分割法基本原理的基础上，通过改变以指数收敛的区间长度缩短比率得到一种新的一维搜索指数优化算法.实例结果表明：该算法的收敛速度要比黄金分割法的收敛速度要快，同时最优解的区间精度也比黄金分割法的要精确；然而，该算法只适用于单峰函数局部最优解的求取.

一维搜索；黄金分割法；加速收敛；指数优化算法

一维搜索中的黄金分割法［1－4］是在一元单峰函数所定义的区间上，按黄金分割率对称取得一系列黄金分割点，然后对分割点所对应的函数值进行计算和比较，利用区间缩小的序列消去原理，最终确定函数的最优解和对应的最优值.最后，稳定地收敛到一个局部极小点.然而，由于区间的长度缩短比率为常数，故其收敛速度较慢.本文根据黄金分割法的基本原理，提出一种改进的一维搜索指数优化算法.

1 指数优化算法

指数优化算法与黄金分割法同样也只适用于单峰函数.在计算过程中，第1次迭代需要计算2个试探点，以后每次迭代只需新算一点，另一点取自上次迭代［1］.其与黄金分割法的主要区别在于区间的长度缩短比率不是以常数进行收敛，而是以计算两次区间差值的指数值进行收敛，由于指数函数的引用，因此构造出一个具有更加光滑的收敛趋势并且更快收敛速度的指数优化算法.

指数优化算法有如下5个主要步骤.

步骤1 给定初始区间［a1，b1］及精度要求ε＞0，计算试探点λ1，μ1，有

然后，计算函数值f（λ1），f（μ1），置y1＝b1－a1，e1＝0，并令k＝1.

步骤2 若bk－ak＜ε，停止计算；否则当f（λ1）＞f（μ1）时，转步骤3，当f（λ1）≤f（μ1）时，转步骤4.

步骤3 置ak＋1＝λk，bk＋1＝bk，λk＋1＝μk，yk＋1＝bk＋1－ak＋1，ek＋1＝yk＋1－yk，并判断ek＋1大小.如果ek＋1＜0.694，有

否则，有

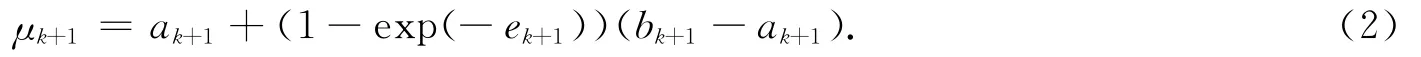
计算函数值f（μk＋1），转步骤5.否则，有λk＋1＝ak＋1＋exp（－ek＋1）（bk＋1－ak＋1）.然后，计算函数值f（μk＋1），转步骤5.

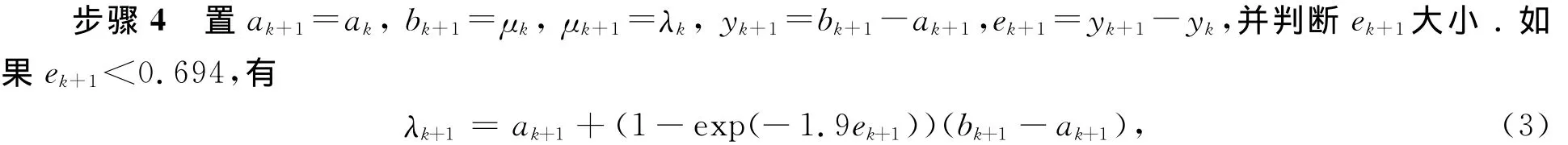
步骤5 置k＝k＋1，返回步骤2.

2 指数系数确定及灵敏度分析

由式（1），（3）可知：指数系数的确定相直接关系到区间收敛的速度.为了确定exp（－Kek＋1）中系数K的大小，可通过MATLAB画出K在区间［0.1，4］，递增量为0.1的一簇负指数曲线.单峰函数的性质区间差呈递减趋势，且当接近最优值的迭代ek基本取于［0，1］区间内，故为了加快收敛速度，取在区间［0，1］值变化比较大的曲线，通过对指数曲线簇进行观察，最终将系数K的取值确定在区间［1，3］之间.对于实例min f（x）＝2x2－x－1，初始区间［a1，b1］＝［－1，1］，精度要求ε≤0.16，对系数K的收敛速度及最优区间的灵敏度进行分析，结果如表1所示.

表1依次计算了K取不同值情况下最优区间和最优解，并最终确定当K＝1.9时为最优，此时最优区间为［0.203 138 02，0.299 143 52］，最优解为0.250 11.据此确定算法中指数系数，并通过以下实例验证，该方法对其他目标函数也是同样适用的.

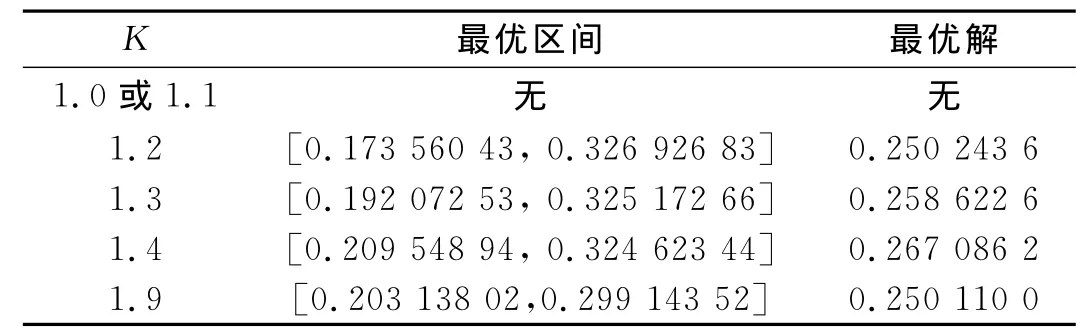
表1 系数的灵敏度分析Tab.1 Sensitivity analysis of Index coefficient

3 算法收敛性证明

定理1［1］设f是区间［a，b］上的单峰函数，x（1），x（2）∈［a，b］且x（1）＜x（2）.如果f（x（1））≤f（x（2）），则对每个x∈［x（2），b］，有f（x）＞f（x（1））；如果f（x（1））＞f（x（2）），则对每个x∈［a，x（1）］，有f（x）≥f（x（2））.

证明 若f（x（1））≤f（x（2）），设极小点为¯x.若x（1），x（2）在¯x的同一侧，根据单峰函数的定义，只有在¯x的右侧，而由于x（1）＜x（2），x∈［x（2），b］，有x（1）＜x（2）≤x，故根据单峰函数定义有f（x）≥f（x（1））；若x（1），x（2）在¯x两侧，因为x∈［x（2），b］，则x与x（2）同侧，故根据单峰函数定义可知f（x）＞f（x（1）），由于f（x（1））≤f（x（2）），则可以推出对每一个x∈［x（2），b］，有f（x）＞f（x（1））.

对于f（x（1））＞f（x（2））情况，同理可证明对每一个x∈［a，x（1）］，有f（x）＞f（x（1））.

定理2 设目标函数f（x）为单峰函数，x∈［a，b］⊂R1，区间缩小的相对精度为ε（ε＞0），经过第k次计算所得到的新的搜索区间为［ak，bk］，记Δk＝bk－ak，则有limΔk＝lim bk－ak≤ε，并且极小点x0在区间［ak，bk］内.

4 实例验证

为了验证指数优化算法的可行性、精度及运算速率，将指数优化法与黄金分割法转化成MATLAB程序加以验证，结果如表2所示.表2中：目标函数为f（x）；实例1为min f（x）＝2x2－x－1，初始区间［a1，b1］＝［－1，1］，精度要求ε≤0.16；实例2为min f（x）＝e－x＋x2，初始区间［a1，b1］＝［－1，1］，精度要求ε≤0.2；程序的运算时间为运行30次的平均值.

表2 指数优化算法和黄金分割法的比较Tab.2 Comparison between exponential optimization method and golden section method

由表2可知：对于实例1，指数优化算法的收敛速度要比黄金分割法的收敛速度要快，同时最优解的区间精度也比黄金分割法的要精确；对于实例2，在最优解区间相近的情况下，指数收敛法的收敛速度依然比黄金分割法的要快.

5 结束语

以黄金分割法的基本原理为基础，提出了一种用于一维搜索的改进的算法——指数优化算法.该方法结合黄金分割法并对其改进，继承了黄金分割法的计算简单的优点，并改善了其收敛速度慢的不足，从而取得了较好的效果.但本算法依然只适用于单峰函数局部最优解的求取，下一步的工作是克服此算法的缺陷，并将算法推广到全局的最优化领域中.

［1］ 陈宝林.最优化理论与算法［M］.北京：清华大学出版社，2005：256－263.

［2］ 徐望宝，陈雪波，李小华，等.快速稳定收敛的一维搜索算法——水平割线法［J］.鞍山科技大学学报，2006，30（2）：356－359.

［3］ 马昌凤.最优化方法及其Matlab程序设计［M］.北京：科学出版社，2008：18－21.

［4］ 王晓陵，陆军.最优化方法与最优控制［M］.哈尔滨：哈尔滨工程大学出版社，2006：10－16.

An Improved Exponential Optimization Algorithm of One－Dimensional Search

ZHANG Zhi－bin1，JIN Fu－jiang1，TANG Yi－ping2，3
（1.College of Information Science and Engineering，Huaqiao University，Xiamen 361021，China；2.College of Mechanical Engineering and Automation，Huaqiao University，Xiamen 361021，China；3.Fujian Fengzhu Textile Science ＆Technology Co.，Ltd.，Quanzhou 362200，China）

Based on the analysis of the basic principle of the golden section method，a new method called exponential optimization algorithm for one－dimensional search was presented by changing the interval length ratio of the exponential convergence.The results show that the method has faster convergence rate than that of the golden section method and the precision interval of the optimal solutions are also better than that of the golden section method.However，this algorithm applies only to calculate the local optimal solution of one－humped function.

one dimension search；golden section method；convergence acceleration；exponential optimization algorithm

O 232

A

（责任编辑：黄晓楠 英文审校：吴逢铁）

1000－5013（2012）05－0503－03

2011－11－22

金福江（1965－），男，教授，主要从事复杂系统建模、仿真与控制的研究.E－mail：jinfujiang＠163.com.

福建省产学研重大科研基金资助项目（2011H6019）