含裂纹故障多自由度齿轮系统的动力学分析
马 锐,陈予恕
(哈尔滨工业大学航天学院,黑龙江哈尔滨 150001)
含裂纹故障多自由度齿轮系统的动力学分析
马 锐,陈予恕
(哈尔滨工业大学航天学院,黑龙江哈尔滨 150001)
为探讨齿轮系统裂纹故障的非线性动力学机理,研究含裂纹故障的四自由度齿轮系统的动力学特性,考虑时变啮合刚度及非线性间隙的影响,建立含裂纹故障的齿轮四自由度啮合耦合动力学模型,分析裂纹故障对系统啮合刚度的影响;采用谐波平衡法给出系统的解析解,分析裂纹故障及齿轮系统参数对齿轮传动系统的动力学行为的影响.结果表明,裂纹故障能够引起齿轮系统的幅值跳跃、分岔现象和系统共振,从而为齿轮箱的设计及裂纹故障的诊断提供依据.
齿轮传动系统;裂纹故障;时变啮合刚度;非线性间隙;谐波平衡法
0 引言
对齿轮箱故障的研究较多,但多数研究的重点在实测信号的故障识别与检测[3-8],而对故障机理的研究较少.另外,对齿轮动力学机理的研究较多,一般在齿轮系统无故障情况下对系统的稳定性、混沌和分岔等机理[9-11]进行研究.文献[12-13]通过有限元法分析裂纹扩展,研究裂纹对系统模态的影响等动力学行为.Wu Shiyan等[14]分析齿轮裂纹程度对啮合刚度的影响,并通过刚度的变化分析裂纹演化的故障机理.Fakher C等[15]考虑裂纹对齿轮啮合刚度的影响.马锐等[16]建立含裂纹故障的齿轮副扭转振动模型,分析齿轮裂纹故障引起的动力学特征.
齿轮裂纹故障主要影响系统的啮合刚度,因此笔者将只考虑刚度的变化,不考虑传动轴等振动的影响,建立含裂纹故障的齿轮—转子—轴承模型,利用谐波平衡法获得系统的各谐波解,分析裂纹故障演化、传动误差及非线性间隙对系统动力学行为的影响.
1 裂纹齿轮系统
1.1 啮合刚度
当轮齿出现裂纹时,势必影响齿轮的啮合刚度,以齿轮裂纹扩展(见图1)为例,采用文献[15]的啮合刚度计算方法得到裂纹对轮齿刚度(见图2)的影响,以裂纹轮齿进入啮合时为初始.依据图1定义裂纹程度h=pc/(2L)×100%,其中pc为裂纹深度,L为裂纹初始点到中心位置的长度.由图2可以看出,裂纹故障的存在对啮合刚度的影响很大,这里对裂纹故障仅考虑刚度变化,并为计算方便,将啮合刚度kg进行傅里叶展开:
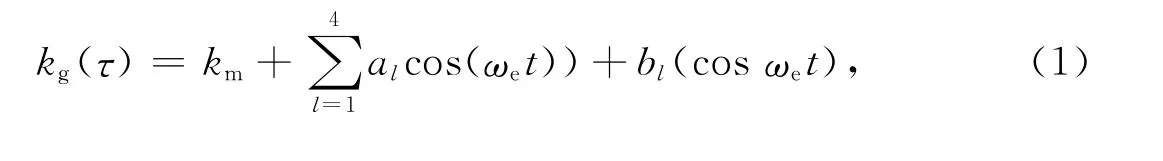
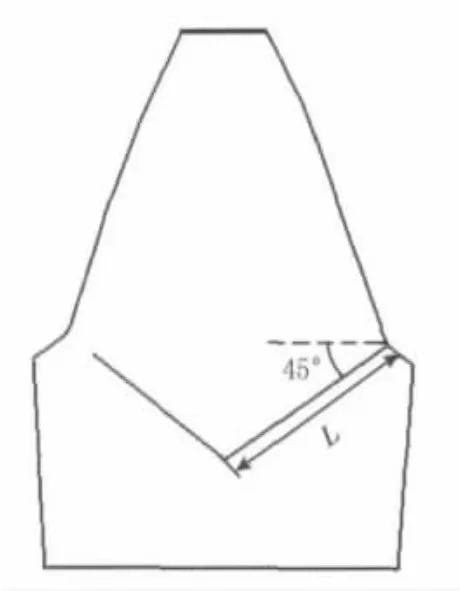
图1 轮齿裂纹的扩展路径
式中:ωe为啮合频率,ωe=z1ω1=z2ω2,z1,z2为齿数,ω1,ω2为恒定角速度;al,bl为谐波系数.

图2 齿轮啮合刚度随裂纹的变化
1.2 裂纹齿轮模型
齿轮—转子—轴承模型简图见图3,轴承及轴可以等效为阻尼和刚度,其中线性阻尼系数为c1及c2,刚度为k1及k2,F1与F2为作用在轴承上的外力.模型考虑静传动误差,将静传动误差e(τ)假设为以啮合频率为周期的周期函数:
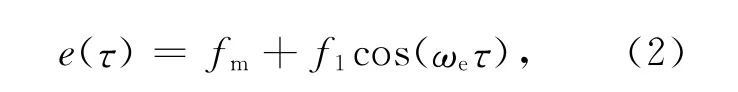
式中:fm为平均静传动误差;f1为静传动误差谐波系数.
基于假设,非线性齿轮—转子—轴承系统的啮合耦合动力学模型表示为
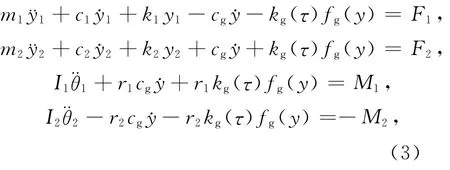
其中传递误差定义为
一是鼓励并引导矿山企业做大做强,以成品化、产业化、基地化为目标,大力延伸矿产开发产业链,重点加强砂石矿产开发与水泥、混凝土等建筑工业的深度融合,推动石料原矿向建筑构件、混凝土等成品化方向延伸发展。
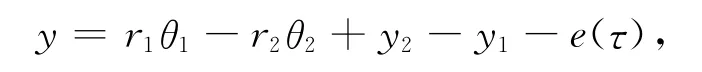
式中:cg为啮合阻尼系数;kg(τ)为轮齿啮合的时变刚度;M1,M2为齿轮的扭矩;F1,F2为作用在轴承上的力;m1,m2为齿轮质量;I1,I2为齿轮转动惯量;r1,r2为齿轮基圆半径;k1,k2为轴承刚度;c1,c2为轴承阻尼;fg(y)为齿侧间隙非线性描述函数,可以拟合为fg(y)=y+ny3[17],其中n为非线性间隙系数.
对方程(3)进行化简得
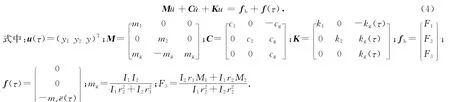
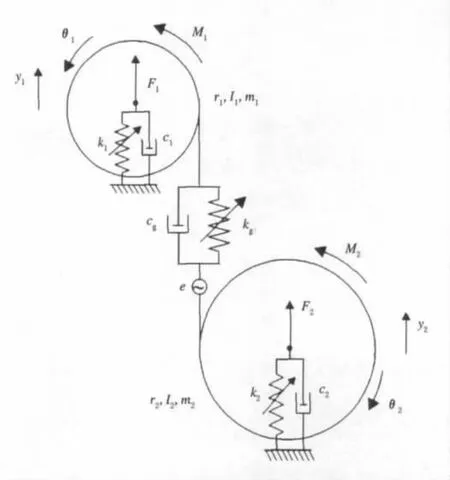
图3 弹性支撑齿轮系统的动力学模型
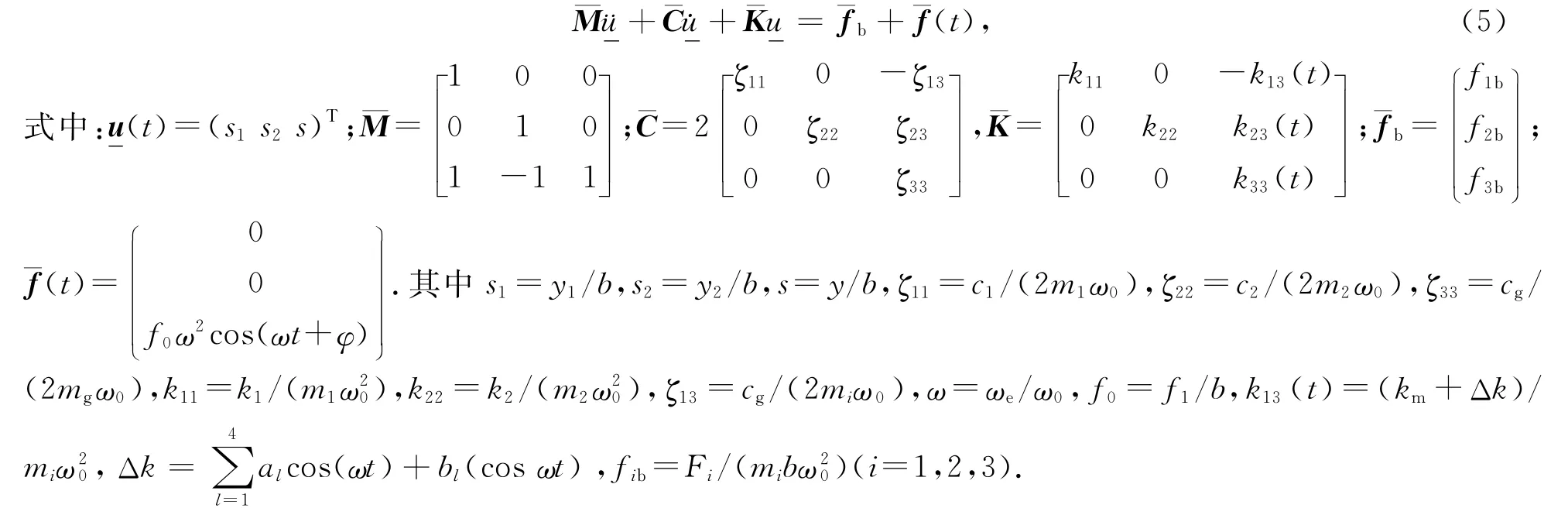
通过线性变换将方程(5)进行变换:
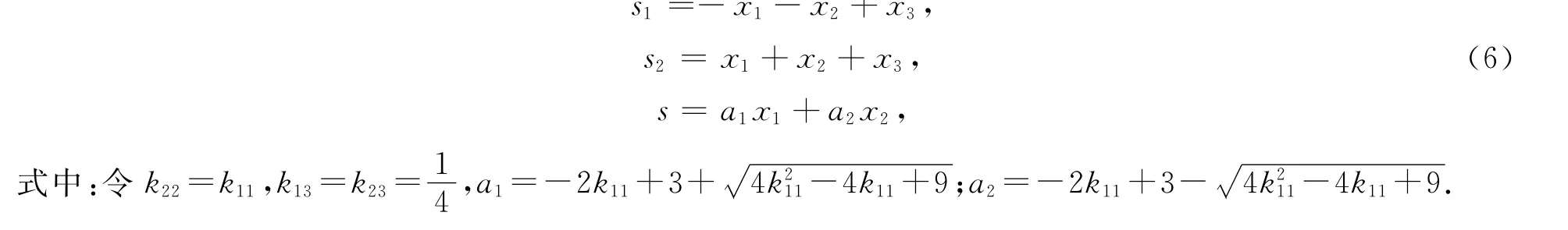
得到2个耦合及1个非耦合方程:
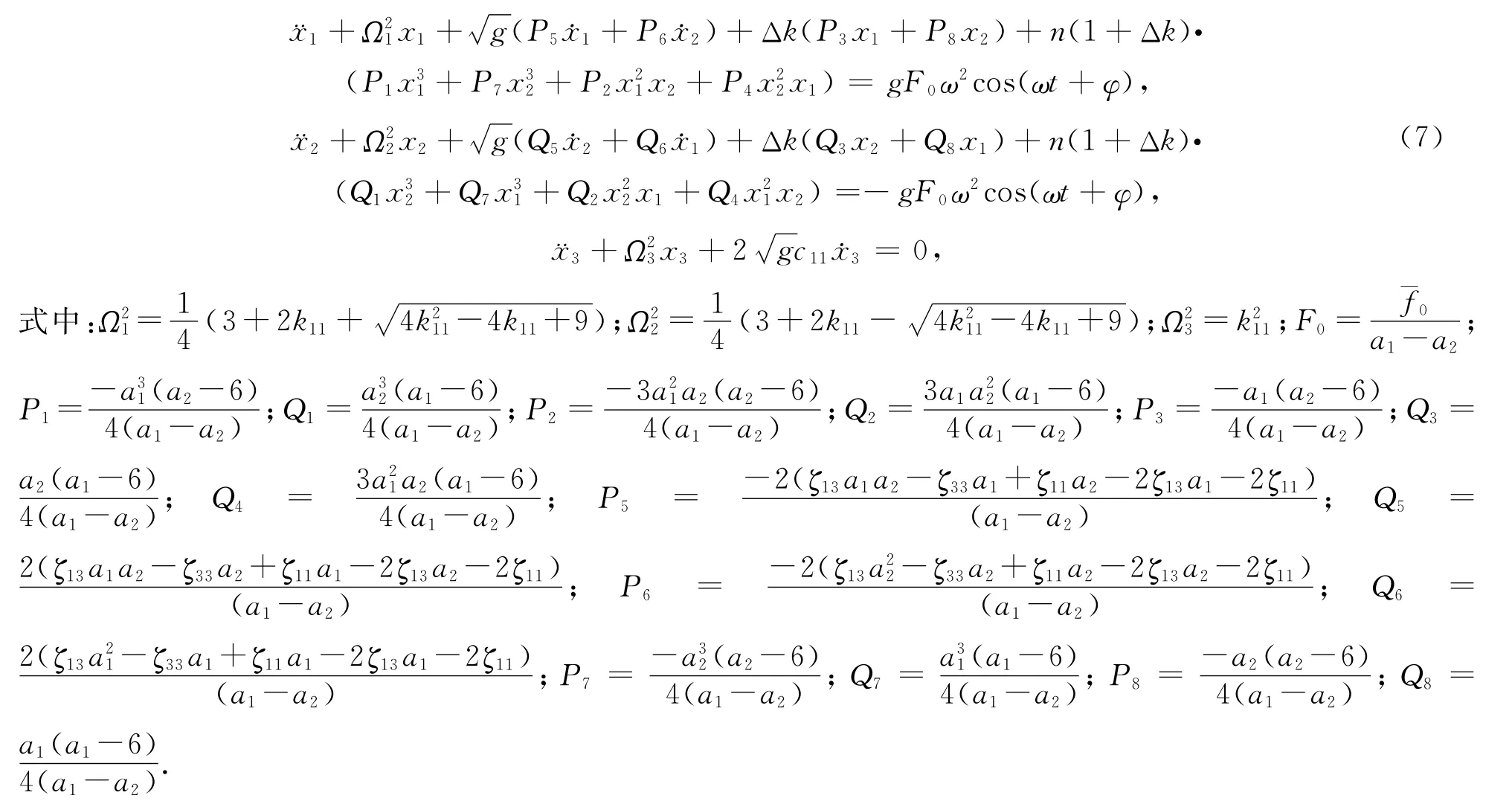
2 动力学分析
由于裂纹动力学方程中的谐波项较多,因此应用谐波平衡法分析多自由度裂纹齿轮系统的动力学行为比较简便.由于高阶谐波的能量较一阶谐波的小,因此仅考虑一阶谐波的情况.由式(7)可以发现第3个方程对系统动力学的分析无影响,因此只讨论前2个方程的解.
设式(7)前2个方程的解是以频率ω周期变化,展开成傅里叶级数:

将式(8)及式(9)代入式(7),令等式左右两边各阶谐波系数相等,得到包含已知和未知系数的6阶代数方程组.通过Newton-Raphson解未知数u=[A0,A1,A2,B0,B1,B2].
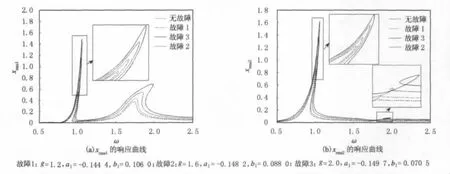
图4 无故障及故障响应曲线
讨论系统参数对齿轮传动系统动力响应的影响,不同F0对系统动力响应的影响见图5,即齿轮系统传动误差的影响.由图5可以看出,F0较小时,xrms1在Ω2处的幅值较Ω1处的小很多,系统非线性不明显;当F0增大时,Ω2处的幅值增加较快,逐渐超过Ω1处的幅值,并出现明显的幅值跳跃,Ω1处仅在较大F0的作用下非线性特性明显.xrms2在Ω2处的幅值始终比Ω1处的大很多.另外,F0也会引起系统的内共振现象.系统的F0较大,即系统的传动误差较大,对系统产生幅值跳跃、内共振等现象,因此在加工及安装齿轮系统时,要减小传动误差的影响.

图5 F0对系统动力响应影响
非线性间隙系数对齿轮系统的影响见图6.由图6可以看出,间隙影响系统的稳定性,也会造成幅值跳跃及内共振现象,因此对齿侧间隙要做适当的调整,控制非线性的发生.
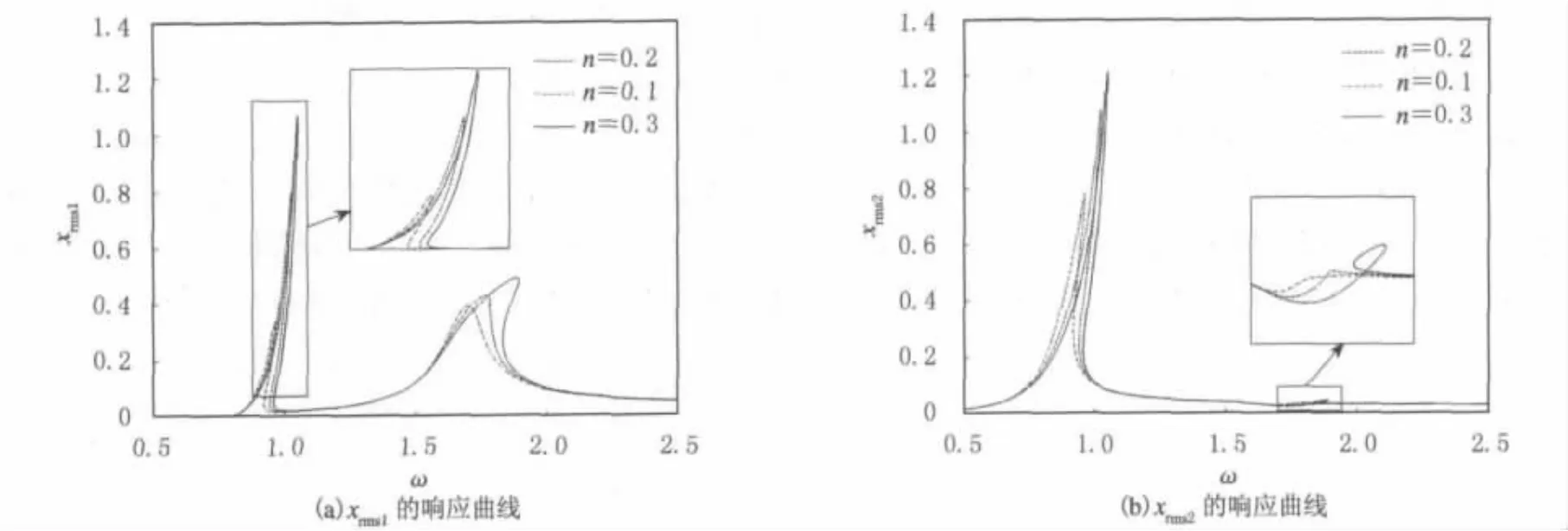
图6 n对系统动力响应的影响
3 结论
(1)考虑裂纹故障对齿轮系统刚度变化引起的内部激励的影响,建立含裂纹故障的齿轮—转子—轴承模型,将模型简化后得到2个耦合及1个非耦合的方程,为解析计算带来方便.
(2)提出由谐波平衡法获得齿轮系统的各谐波解,分析裂纹故障的演化对系统动力行为的影响,以及裂纹故障引起系统的不稳定、幅值跳跃及分岔线性,并且随着裂纹程度的加深,其共振区的幅值增大明显,引起系统的内共振.
(3)分析传动误差及非线性间隙对齿轮系统动力行为的影响,发现非线性间隙及传动误差引起系统的非线性.对于部件较多的多自由度系统,设计不合理时将引起系统的内共振现象,在工程中应尽量避免.
(4)对齿轮进行合理设计,控制加工精度,及时发现故障,为齿轮系统裂纹故障的诊断提供依据.
[1] 陈予恕.机械故障诊断的非线性动力学原理[J].机械工程学报,2007,43(1):25-34.
[2] 丁康,李巍花,朱小勇.齿轮及齿轮箱故障诊断实用技术[M].北京:机械工业出版社,2005.
[3] 赵击文,冯志华,孔凡让.基于混沌理论的设备状态监测应用研究[J].振动工程学报,2004,17(1):78-81.
[4] 王洪刚,郑海起,马吉胜,等.变速箱故障声压信号的小波包分解与诊断[J].振动与冲击,2001,20(2):61-63.
[5] 何田,林意洲,郜普刚,等.局部均值分解在齿轮故障诊断中的应用研究[J].振动与冲击,2011,30(6):196-201.
[6] 刘树林,赵海峰,齐波,等.基于经验模态分解及自相关分析的微弱信号提取方法[J].大庆石油学院学报,2007,31(5):80-84.
[7] 丛蕊,高学良,刘树林,等.EMD和关联维数在往复压缩机故障诊断中的应用[J].大庆石油学院学报,2008,32(2):86-89.
[8] 吕凤霞,别锋锋,曾文,等.基于振动可视化的机械系统级故障诊断方法[J].大庆石油学院学报,2011,35(4):77-82.
[9] Liu Haixia,Wang Sanmin,Guo Jiashun.Solution domain boundary analysis method and its application in parameter spaces of nonlinear gear system[J].Chinese Journal of Mechanical Engineering,2011,24(3):507-513.
[10] 郜志英,沈允文.间隙非线性齿轮系统周期解结构及其稳定性研究[J].机械工程学报,2004,40(5):17-22.
[11] 李润方,王建军.齿轮系统动力学——振动、冲击、噪声[M].北京:科学出版社,1997.
[12] Urala,Heber G.Three-dimensional,parallel,finite elementsimulation of fatigue crack growth in a spiral bevel pinion gear[J].Engineering Fracture Mechanics,2005(72):1148-1170.
[13] Li C J,LEE H.Gear fatigue crack prognosis using embedded model,gear dynamic model and fracture mechanics[J].Mechanical Systems and Signal Processing,2005(19):836-846.
[14] Wu Shiyan,Zuo M J,Anand P.Simulation of spur gear dynamics and estimation of faultgrowth[J].Journal of sound and vibration,2008,317:608-624.
[15] Fakher C,Tahar F.Analytical modeling of spur gear tooth crack and influence on gear mesh stiffness[J].European Journal of Mechanics A/Solids,2009,28:461-468.
[16] 马锐,陈予恕.含裂纹故障齿轮系统的非线性动力学研究[J].机械工程学报,2011,47(21):84-90.
[17] Theodossiades S,Natsiavas S.Non-linear dynamics of gear-pair systems with periodic stiffness and backlash[J].Journal of Sound and Vibration,2000,229(2):287-310.
Dynamic analysis of multi-freedom gear system with cracked failure/2012,36(3):110-114
MA Rui,CHEN Yu-shu
(School of Astronautics,Harbin Institute of Technology,Harbin,Heilongjiang150001,China)
This study focuses on the dynamic characteristics of the four-freedom gear system with local crack defectto explore the crack nonlinear dynamic mechanism.The dynamic model of the gear system with crack defect,time-variantmesh stiffness and nonlinear clearance are established to investigate the effectof crack defecton mesh stiffness.The dynamic characteristics with the evolvementof crack and other system parameters are studied by employing harmonic balance method,which reveals the amplitude jump,bifurcation phenomenon and internal resonance.The results obtained herein can provide a theoretical basis for the design and crack faultdiagnosis of gearbox.
gear system;cracked failure;time-variantmesh stiffness;nonlinear clearance;harmonic balance method
book=3,ebook=48
TH132.4
A
1000-1891(2012)03-0110-05
2012-03-20;编辑:任志平
国家自然科学基金重点项目(10632040)
马 锐(1982-),女,博士研究生,主要从事非线性动力学、机械设备故障诊断方面的研究.

