基于FFT的扩频通信系统抗干扰技术研究
张银蒲,孙茂松,窦桂华
(唐山学院信息工程系,河北唐山063000)
基于FFT的扩频通信系统抗干扰技术研究
张银蒲,孙茂松,窦桂华
(唐山学院信息工程系,河北唐山063000)
针对无线信道中的高斯白噪声、窄带干扰问题,采用重叠变换的FFT频域陷波算法对相关干扰进行削弱或消除,并将其在扩频通信系统中进行了仿真分析。结果表明,这项技术可使受干扰后的频谱泄露大大降低,从而减少了信号的损伤,提高了信息传输的准确性、可靠性。
抗干扰技术;重叠变换的FFT频域陷波算法;扩频通信
扩频通信用扩展频谱的方法换取较高信噪比,具有较传统无线通信方式无可比拟的优势。无线通信系统中信息的传输要受到移动无线信道的制约,而信道中不可避免的会存在一些干扰,如果干扰太强,当超出系统的干扰容限时,系统将无法正常工作。扩频通信系统本身有一定的抗干扰能力,但在有较强干扰的情况下,尤其是在有意的敌对干扰环境下,干扰强度很容易超出其干扰容限[1],这就需要采取相关技术来增强系统的抗干扰能力,而干扰抑制技术是一种很有效的措施。
1 基于FFT的扩频通信的信道抗干扰技术
扩频通信系统中的无线信道是极其复杂的,路径损失、信号的多径传输以及移动引起的接收信号频移等都会使信号产生衰落。当然,信道中也会存在一些人为和非人为的干扰。高斯白噪声就是一种不可避免的噪声,只能削弱而不能完全消除;窄带干扰是一种人为加入信道的干扰,它的功率可以特别大,足以淹没干扰频段的信号信息,是无线通信的巨大障碍,对此必须进行削弱或消除。
干扰抑制技术通常是利用信号和干扰在时域和频域的特性差别来检测和消除干扰。一般来说,在干扰抑制技术中,可利用的信号和干扰信息越多,则获得的干扰抑制技术性能就越好。[2]
目前常用的干扰抑制技术主要分为基于预测的干扰抑制技术和变换域的干扰抑制技术。其中,变换域干扰抑制技术主要指在变换域进行的干扰信号的检测和消除,包括基于FFT、基于重叠变换LT、基于时频域变换的干扰抑制技术。基于FFT的干扰抑制技术具有能有效地对付多音干扰,随干扰的变化调整迅速,且易于工程实现的优势,因此,对基于FFT的干扰抑制技术的研究具有重要意义。
1.1 变换域的干扰抑制算法原理
变换域的干扰抑制技术主要是利用窄带干扰的功率谱集中在很窄的频带中,通过傅里叶变换,将干扰映射到很窄的变换域子带,通过设置阈值和门限检测出干扰的位置,控制开关将相应的子带分量置零,从而达到减轻或抑制干扰的目的。其原理图如图1所示。

图1 变换域窄带干扰抑制原理图
在变换域抗干扰技术方面,尽管基于取舍的体制从根本上说是自适应的,但典型的处理方法是在判断出干扰的位置后,对各个变换域系数乘以权0或权1,即去除含干扰的变换域系数,保留不含干扰的变换域系数。因此,采用连续变换的权值并使用某种优化算法来调节权值,可以最大程度地改善系统性能。
由于变换域抗干扰方法具有很多优点,因此被认为是一种极具潜力的抗干扰策略,在时域很复杂的滤波过程中可以通过频域简单的相乘来完成,而且时域无法实现的理想滤波器传递函数,如矩形滤波器等,也可以很方便地在频域实现。在扩频通信领域,变换域处理技术可以有效地抑制干扰并改善系统性能。
1.2 FFT重叠变换干扰抑制算法
快速傅立叶变换(FFT)方法有:时间抽选基2FFT算法(库里-图基算法)、频率抽选基2FFT算法。
时间抽选基2FFT算法(库里-图基算法):
设N=2M,M为正整数,把离散时间序列按时间进行奇偶分解
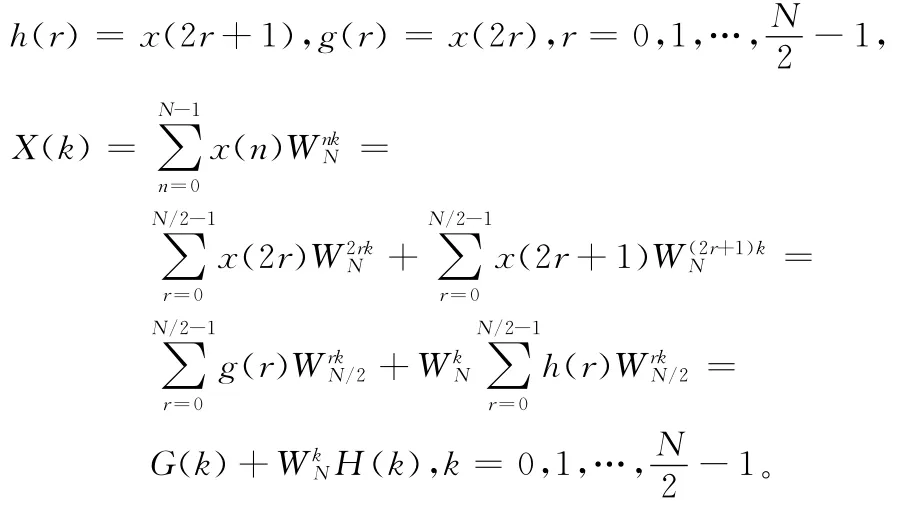
由上式可求出N/2个点的离散傅立叶变换。
后N/2个点的离散傅立叶变换为
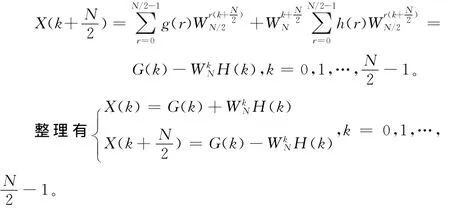
信号流图如下:
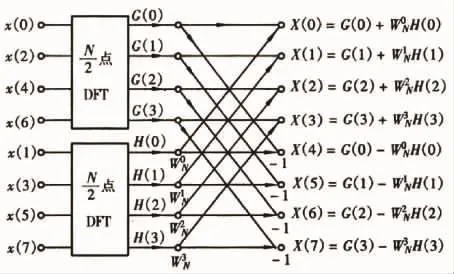
对G(k)和H(k)采用上述同样的奇偶分解方式,可分别得

对M(k),N(k),P(k)和Q(k)均采用上述同样的奇偶分解方式,可分别得N/8,N/16个点等等的离散傅立叶变换,依次类推,最后到2个点的离散傅立叶变换。
最后两点的离散傅立叶变换

FFT具有M级、N/2个碟形运算。
频率抽选基2FFT算法原理与时间抽选基2FFT算法原理相似,不同之处在于它是把输出序列X(k)按其顺序的奇偶分解为越来越短的序列。
FFT重叠变换干扰抑制算法的原理是窄带干扰相对于扩频信号能量集中在很窄的频带内,在频域上就表现为很窄的尖峰,所以可先将混合信号变换到频域,检测出干扰的频谱位置,将这些谱线去掉或进行衰减,最后反变换还原成时域信号进行解扩。[4]其原理框图如图2所示。
FFT重叠变换干扰抑制算法不需要自适应算法,且其处理速度远远超过时域滤波的算法。

图2 频域陷波技术实现框图
FFT重叠变换干扰抑制技术实现的数学模型如图3所示。

图3 频域陷波技术实现的数学模型
图3中,W(n)是窗函数,abs(u)和angle(u)两个函数分别求离散傅里叶变换后幅度和角度(相位)值,Thre(u)函数确定谱线的门限值,p(u)函数是对谱线进行处理。
2 抗干扰技术仿真与分析
仿真结果的各个波形图如图4所示。
由图4(a)和4(b)可以看出,窄带干扰基本被抑制了,图4(b)已经可以比较清晰地看到信号的相位翻转情况,但是由于噪声存在(干扰抑制算法无法抑制噪声影响),干扰抑制后的信号波形还有一定的起伏;图4(c)是1/4重叠复用频域陷波模块各支路抗窄带干扰后的波形及4路对齐叠加之后的信号波形,该波形图横坐标单位为“s”,纵坐标单位是“V”。由图可见其帧信号两端的衰减在对齐合并之后消失了;图4(d)为含窄带干扰信号经过重叠变换频域陷波之后的信号频谱图。频域陷波算法进行了加窗处理和1/4重叠变换,该措施使干扰的频谱泄露大为降低,也使信号的损伤大为减少,这些因素促成了该算法良好的抗窄带干扰性能。
在变换域干扰抑制技术中,基于FFT的干扰抑制技术优点是能够处理多个干扰,并且可以快速跟踪干扰的变化。它在设计干扰抑制算法时更自由,能提供更大的动态范围,抑制干扰的数目仅与FFT变换长度有关。通过合理选择窗函数和抑制算法,陷波深度可以非常大。由于FFT对接收数据的每一个记录进行变换,因此实时FFT算法有能力对变化的干扰环境快速自适应。

图4 抗干扰技术仿真波形图
3 结论
扩频通信以其较强的抗干扰、抗衰落、抗多径性能而成为第三代通信的核心技术。[5]将基于FFT的干扰抑制技术用于扩频通信系统,可使干扰的频谱泄露大大降低,减少信号的损伤,由此提高了信息传输的准确性、可靠性。
参考文献:
[1] 杜思深,唐书娟.抗干扰通信与电子攻击的发展[J].中国新通信,2009(15):68-70.
[2] 于江,王春岭,沈刘平,等.扩频通信技术原理及其应用[J].中国无线电,2010(03):44-47.
[3] 程佩青.数字信号处理教程[M].北京:清华大学出版社,2001.
[4] 赵刚.扩频通信系统实用仿真技术[M].北京:国防工业出版社,2009.
[5] 靳丽平,韩慧莲.直接序列扩频通信系统研究及仿真[J].电子测试,2011(1):78-72.
(责任编校:夏玉玲)
Research on Anti-Jamming Technology in Spread Spectrum Communication System
ZHANG Yin-pu,SUN Mao-song,DOU Gui-hua
(Department of information Engineering,Tangshan College,Tangshan 063000,China)
For interference of Gaussian white noise and narrowband in wireless channel,overlap conversion FFT frequency domain notch filter algorithms can be adopted to reduce or eliminate relevant interference.Simulation analysis can be conducted in upon it in spread spectrum communication system.Results show that the technology can greatly reduced the interference spectrum leak and the signal damage and it improves the accuracy and reliability of information transmission.
anti-jamming technology;overlap conversion FFT frequency domain notch filter algorithms;spread spectrum communication
book=17,ebook=17
TN914.42
A
1672-349X(2012)03-0097-03
2012-03-16;
:2012-03-29
张银蒲(1978-),女,河北保定人,讲师,硕士,主要从事信号处理、控制工程研究。

