裂缝型HTI介质中的弹性阻抗
窦喜英,韩立国,刘春成,杨小椿
1.吉林大学地球探测科学与技术学院,长春 130026 2.中国海洋石油研究总院,北京 100027
裂缝型HTI介质中的弹性阻抗
窦喜英1,韩立国1,刘春成2,杨小椿2
1.吉林大学地球探测科学与技术学院,长春 130026 2.中国海洋石油研究总院,北京 100027
在回顾封闭平行硬币状裂缝模型的基础上,将裂缝填充物性质、分布密度与背景介质的横纵波速度比,引入裂缝型水平横向各向同性介质纵波、转换横波弹性阻抗公式,并进行归一化弹性阻抗响应特征模拟。分析表明:裂缝介质弹性阻抗呈现方位各向异性,且随裂缝密度加大而增强;纵波、转换横波弹性阻抗在值域分布规律上具有较大区别;在典型砂岩介质的前提下,弹性阻抗差可以作为裂缝含气、含水指示因子定性地识别裂缝填充物性质。
弹性阻抗;裂缝;填充物;裂缝密度;横纵波速度比
0 引言
基于AVO理论,弹性阻抗属于叠前反演的范畴。自1999年Connolly[1]提出各向同性介质纵波弹性阻抗的概念以来,弹性阻抗理论得到迅速发展,一系列具有明显物理意义的概念被相继推出,如Landro等[2]、Kenneth等[3]先后提出的横波弹性阻抗,Whitcombe等[4-5]提出的归一化弹性阻抗、扩容性弹性阻抗,马劲风[6]提出的广义弹性阻抗,Martins[7]提出的各向异性弹性阻抗等。在上述概念的基础上,Ma等[8]基于Zoeppritz方程推导了转换横波弹性阻抗的精确表达形式,苑书金等[9]推导了垂直横向各向同性(vertical transversely isotopic,VTI)介质的纵波弹性阻抗公式,陈天胜等[10]对水平横向各向同性(horizontal transversely isotopic,HTI)介质的纵波弹性阻抗进行了研究,Jilek[11-12]基于弱各向异性的转换横波反射系数公式推导出复杂的P-SV波、P-SH波弹性阻抗公式,崔杰等[13]基于简化的Jilek反射系数公式重新推导了新的各向异性转换波弹性阻抗公式。
在应用领域,相比声波阻抗,弹性阻抗在一定程度上克服了零炮检距的限制,在描述地质体的分布特征,提取纵横波阻抗、速度、速度比、密度、泊松比等多种属性,以及预测岩性和流体等方面的能力和精度得以较大提高,因此受到广泛关注[14-17]。但对各向异性较强的裂缝型油气藏而言,检测裂缝密度、裂缝方位角以及裂缝填充物性质是其主要工作。目前,严格意义上基于各向异性理论的裂缝检测技术有P波振幅、速度、旅行时、S波以及多波多分量技术[18],而基于弹性阻抗的裂缝检测技术限于公式参数较多,且物理意义不直观,难以形成技术服务于生产需要。
笔者在回顾Hudson裂缝模型的基础上,根据裂缝弹性参数与广义Thomsen各向异性参数的关系[19],对HTI介质P波弹性阻抗公式、P-SV波弹性阻抗公式进行裂缝参数化改造,建立起裂缝介质参数与弹性阻抗的显式关系,通过数值模拟分析气饱和与水饱和填充的2种条件下,裂缝密度对弹性阻抗的影响规律。
1 Hudson裂缝理论
Hudson[20-21]提出封闭平行硬币状裂缝模型,认为实际裂缝介质可以用如下模型等效,即各向同性背景中发育着一组或者多组互相平行的垂直裂隙。该模型涉及的主要参数为围岩的横、纵波速度与密度,裂缝分布密度与排布方位角,裂缝填充物的横、纵波速度与密度。作为该类模型的核心参数,裂缝分布密度e=Nr3/V,其中V是介质基质的体积,r是裂隙圆片的半径,N为总体积内裂隙圆片的总个数。这种宏观背景参数结合微观裂缝参数的描述方式,使Hudson模型比其他等效模型,如线性滑动模型[22-24]、部分流体饱和裂缝模型[25-27],能够更直观地、量化地刻画裂缝型介质及其波场[28]。作为Hudson模型的特例——单组裂缝的HTI模型,因其相对简单且有代表性,被学术界广泛地运用于方位各向异性理论以及裂缝型油气藏的研究中。
在广义Thomsen系数[29]基础上,Bakulin等[19]建立了HTI模型中裂缝弹性参数与广义Thomsen系数的函数关系,如表1所示。其中vP2、vS2分别为下层HTI介质的垂直纵、横波速度。分析可知,广义Thomsen系数是裂缝密度e和横、纵波速度平方比g的简单函数,除γ(V)外,各参数对裂缝填充物性质敏感。

表1 裂缝弹性参数与广义Thomsen系数的函数关系Table 1 Relations between crack parameters and generalized Thomsen’s coefficients
由此推论,裂缝填充物、裂缝密度、围岩的横、纵波速度比作为裂缝型油气藏检测的重要参数,控制了弹性波场的各向异性性质,且有可能对弹性阻抗造成影响。为探索可能的规律,笔者将上述关系引入纵波、转换横波弹性阻抗公式,并进行数值模拟。
2 HTI介质弹性阻抗
2.1 HTI介质的纵波弹性阻抗
陈天胜等[10]沿用Connolly推导弹性阻抗公式的方法,从Rüger[29-30]给出的弱各向异性反射系数近似公式出发,推导出以广义Thomsen系数为基础的HTI介质纵波弹性阻抗公式:
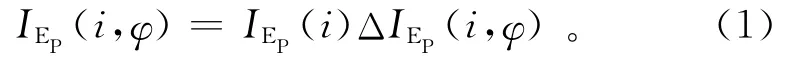
其中:IEP(i,φ)为各向异性纵波弹性阻抗;IEP(i)为各向同性背景项;ΔIEP(i,φ)为各向异性扰动项(各向异性因子);i为入射角;φ为方位角。
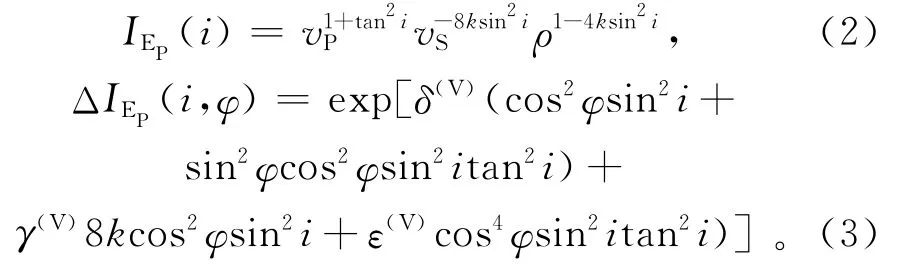
其中:ρ=(ρ2+ρ1)/2;vP=(vP1+vP2)/2;vS=(vS1+vS2)/2;k=[(vS1/vP1)2+(vS2+vP2)2]/2;ρ1,ρ2,vP1,vP2,vS1,vS2分别为上、下层介质的密度,纵波速度和横波速度。
将表1中各式分别代入式(1)-(3),最终得到相应的气饱和裂缝、水饱和裂缝条件下HTI介质纵波弹性阻抗公式,由此建立起弹性阻抗与裂缝参数的显示关系:
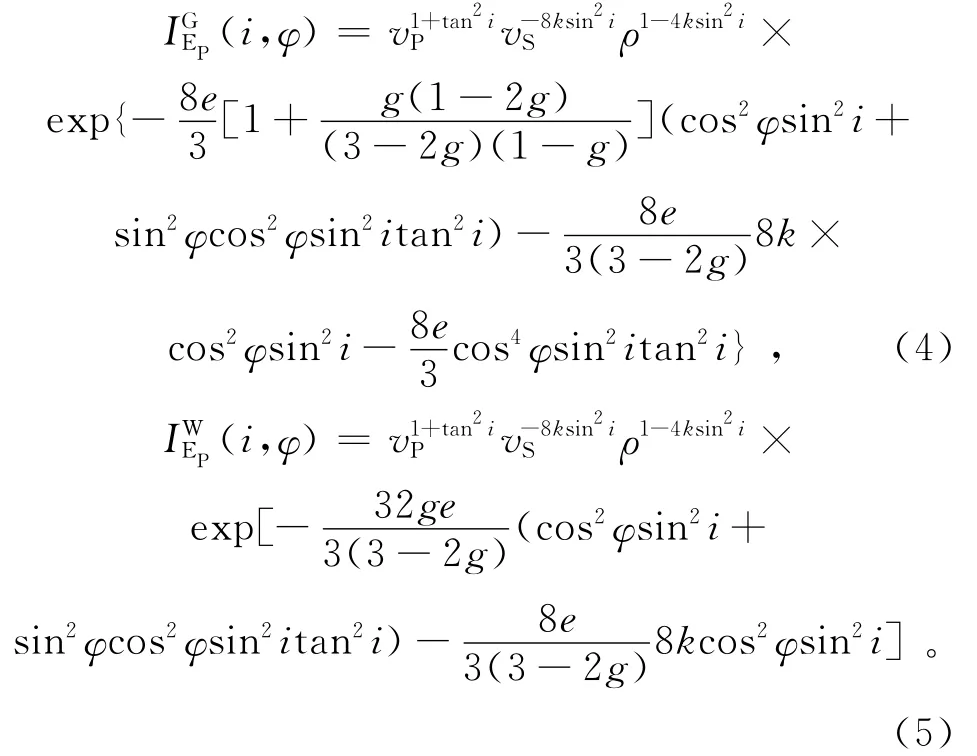
2.2 HTI介质的转换横波弹性阻抗
Petr Jilek[11-12]从一阶摄动理论出发,根据推导弱各向异性介质中PP反射-透射系数的方法推导出弱各向异性介质中PS波反射系数公式;崔杰等[13]在保证精度的基础上对正交各向异性介质中P-SV波反射系数公式进行了简化,保留sini的三次幂,并对各向异性参数进行了转换,得到HTI介质中P-SV波弹性阻抗的近似公式:
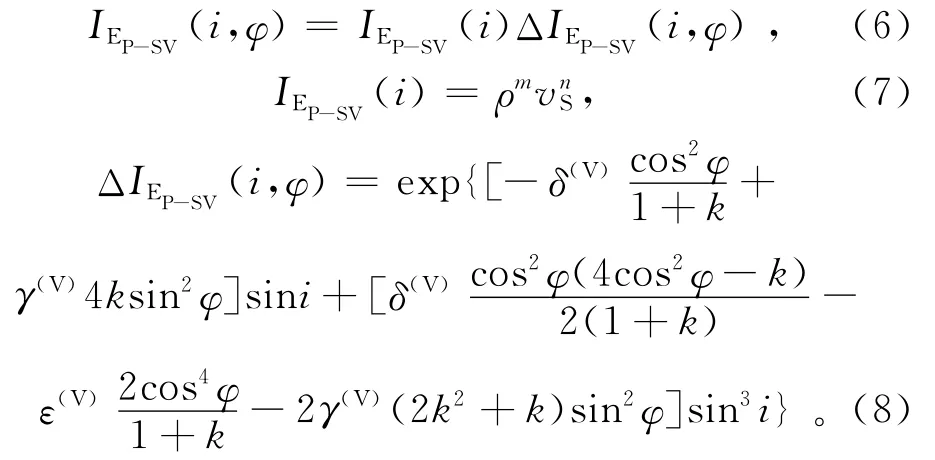
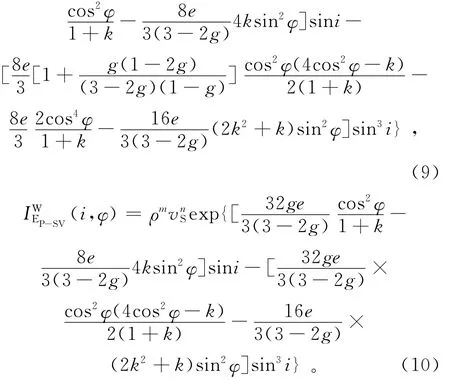
3 数值模拟
Hudson理论认为,裂缝密度是裂缝介质中波场各向异性性质的主控因素,而裂缝填充物性质对纵波、转换横波的影响程度各不相同[27]。为了评估(i,φ)平面内e和g对弹性阻抗的影响,分3步进行数值试验:
1)改造了Barnola等[31]使用的第一类AVO模型,即上覆各向同性盖层为页岩,下层裂缝介质为含水、含气2类砂岩,模型示意图参见图1。
其中:IEP-SV(i,φ)为HTI介质的各向异性转换横波弹性阻抗;IEP-SV(i)为各向同性转换横波弹性阻抗;ΔIEP-SV(i,φ)为HTI介质各向异性扰动因子;m=
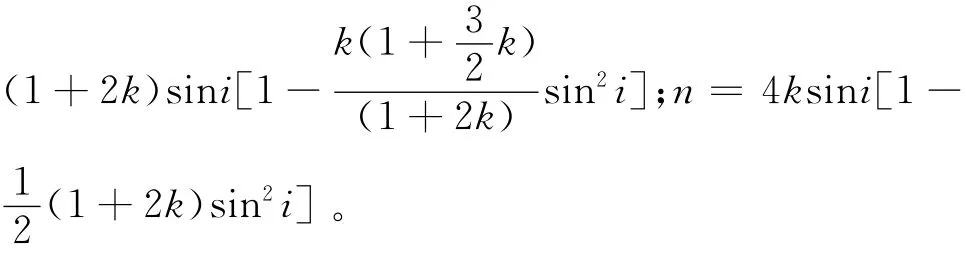
将表1中各式分别代入式(6)-(8),即可得到含气和含水裂缝条件下转换横波弹性阻抗公式:
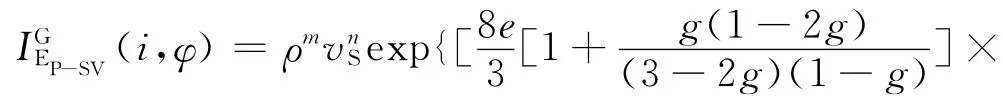
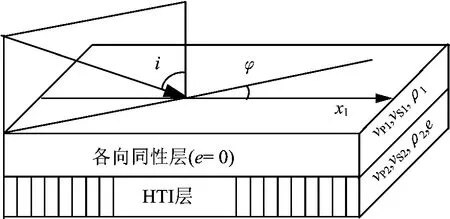
图1 模型示意图Fig.1 Sketch of model
2)设计试验流程如图2所示:①以下层介质为基准(e取0),计算各向同性归一化弹性阻抗;②修改下层介质为HTI介质(e取0.1,0.15,0.20),计算各向异性归一化弹性阻抗;③将第②步所得阻抗与第①步所得阻抗相减得到弹性阻抗差。模型参数参见表2。
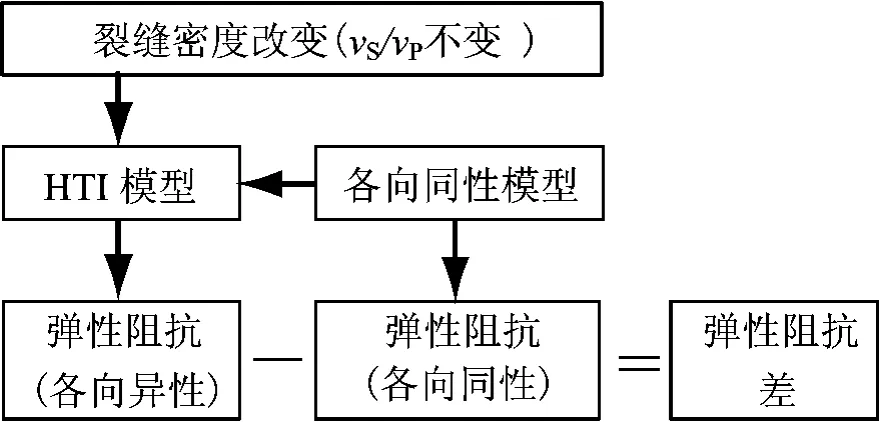
图2 数值模拟分析流程示意图Fig.2 Flow of model
3)将上述模型参数与计算步骤分别应用于纵波、转换横波弹性阻抗公式,得到i∈(0,30°)、φ∈(0,90°)区域内水饱和、气饱和裂缝介质的弹性阻抗差展布图,其中:纵波弹性阻抗差如图3a1、a2所示,转换横波弹性阻抗差见图3a3、a4;为了进一步说明弹性阻抗的方位性与周期性,进一步抽取相应模型在i=30°、φ∈(0,360°)时的弹性阻抗差,取其绝对值后显示在极坐标系下,结果如图3b1、b2、b3和b4所示。
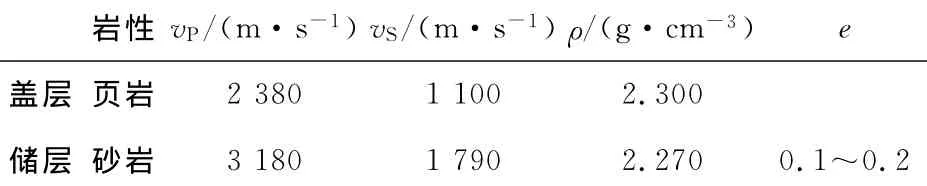
表2 第一类AVO类型的岩性参数(据文献[31]模型修改)Table 2 Parameters for AVO 1st(modified from reference[31])
图3a1、a2中,纵波弹性阻抗差随着方位角、入射角与裂缝密度、裂缝填充物性质的变化而变化。在方位角方面,弹性阻抗差以360°为周期呈现方位变化。当φ由0°向90°变化时,弹性阻抗差的绝对值单调递减,即方位各向异性特征减弱。其中:φ=0°时,对应的弹性阻抗差最大,即阻抗各向异性最强;φ=90°时的弹性阻抗差为0,即阻抗为各向同性。在入射角方面,临界角范围内,弹性阻抗差的绝对值随着入射角增大而单调增大。其中:当i=0°时,弹性阻抗差为0,即零偏移距时无AVO特征显示;当i=30°时,弹性阻抗差最大,即偏移距最大时AVO特征最明显。在裂缝密度方面,弹性阻抗差随着裂缝密度增大而负向增大。在填充物性质方面,含水裂缝的弹性阻抗差数值最高约为500,约占相应各向同性弹性阻抗值的8%;而含气裂缝的对应值分别为750与12%。该特性可以作为砂岩裂缝中气、水识别的初步依据。
由图3a3、b3、a4、b4可知,与纵波弹性阻抗差相比,转换横波的弹性阻抗差保持了方位各向异性特征,随入射角增大而增大和各向异性随裂缝密度增大而增强等性质。区别在于:在变化趋势上,转换横波的弹性阻抗差随裂缝密度的增大,其增大趋势呈现正向,并非纵波弹性阻抗差的负向;弹性阻抗差随入射角、方位角的变化会出现符号反转现象,并非纵波弹性阻抗差单调负向增加。在数值上,转换横波弹性阻抗差小于纵波,水填充裂缝介质的弹性阻抗差最高约为130,约占相应各向同性弹性阻抗值的4%,而气填充裂缝的对应值分别为330与10%。由此推论,利用转换横波弹性阻抗差识别裂缝中气与水,预测结果将比纵波弹性阻抗更准确。
由上述分析可知,裂缝型储层的纵波、转换横波弹性阻抗呈现明显的方位各向异性特征,属于方位各向异性理论范畴。在实际应用中,叠前超道集抽取对资料的基本要求是全方位、高覆盖次数、高信噪比,而主流的采集技术最高只能做到宽方位角、工区中心区域高密度采集。为保证信噪比,在储层反演过程中,往往采用部分方位角叠加的方式,这进一步加重方位信息的损失,降低方位预测结果的可信度。上述原因导致弹性阻抗在提取弹性属性、识别流体方面的特性得不到充分发挥。值得一提的是,全方位、高密度的资料采集技术迅速兴起,并在生产实践中取得良好效果,这对推动利用方位弹性阻抗进行裂缝检测与流体预测具有积极意义[32]。
4 结论
综上所述,裂缝介质弹性参数与广义Thomsen各向异性系数之间存在函数关系,用裂缝介质参数重新描述的HTI介质纵波、转换横波弹性阻抗公式,在理论上验证了裂缝型储层中弹性阻抗方位各向异性的存在,并对其进行量化。通过水平层状模型数值模拟与分析认为,在裂缝型油气藏中,裂缝分布密度控制了弹性阻抗的各向异性性质:裂缝分布密度越大,各向异性越强;填充物性质对弹性阻抗影响的幅度有较大区别,其中含气裂缝要远大于含水裂缝。另外,由于转换横波弹性阻抗差比纵波更加显著,在横波资料准确的前提下,利用转换横波识别裂缝流体类型,将会比纵波更可靠。
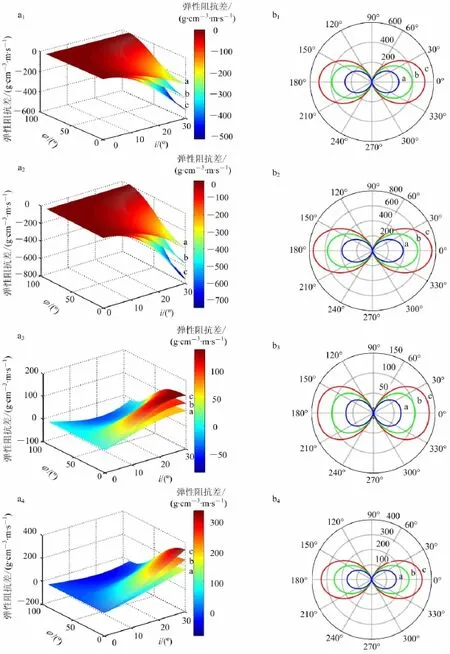
图3 裂缝HTI介质的弹性阻抗差Fig.3 Elastic impedance differences for cracked HTI media
参考文献(References):
[1] Connoly P.Elastic Impedance[J].The Leading Eage,1999,18(4):438-452.
[2] Landro M,Duffaut K,Rogno H.Well Calibration of Seabed Seismic Data[C]//69th Annual Internet SEG Mtg.Denver:[s.n.],1999:860-863.
[3] Duffaut K,Landro M,Rogno H.Shear Wave Elastic Impedance[J].The leading Edge,2000,19:1223-1229.
[4] Whitcombe D N.Elastic Impedance Normalization[J].Geophysics,2002,67(1):60-62.
[5] Whitcombe D N,Connolly P,Reagan R L.Extended Elastic Impedance for Fluid and Lithology Prediction[J].Geophysics,2002,67(1):63-67.
[6] 马劲风.地震勘探中广义弹性阻抗的正反演[J].地球物理学报,2003,46(1):118-124.
Ma Jin-feng.Forward Modeling and Inversion Method of Generalized Elastic Impedance in Seismic Exploration[J].Chinese Journal of Geophysics,2003,46(1):118-124.
[7] Martins J L.An Approach for Elastic Impedance in Weakly Anisotropic Media[C]//72th Annual Internet SEG Mtg.Salt Lake:[s.n.],2002:185-188.
[8] Ma Jin-feng,Morozov Igor B.The Exact Elastic Impedance for P-SV Wave[C]//77th Annual Internet SEG Mtg.San Antonio:[s.n.],2007:288-292.
[9] 苑书金,于长青.各向异性介质中的弹性阻抗及其反演[J].地球物理学进展,2006,21(2):520-523.
Yuan Shu-jin,Yu Chang-qing.Elastic Impedance and Seismic Inversion in Anisotropic Media[J].Progress in Geophysics,2006,21(2):520-523.
[10] 陈天胜,魏修成,刘洋.一种新的各向异性弹性阻抗近似公式[J].石油物探,2006,45(6):563-569.
Chen Tian-sheng,Wei Xiu-cheng,Liu Yang.New Approximation Formula for Calculation of Elastic Impedance in Anisotropic Media[J].Geophysical Prospecting for Petroleum,2006,45(6):563-569.
[11] Jilek P.Converted PS-Wave Reflection Coefficients in Weakly Anisotropic Media[J].Pure and Applied Geophysics,2002,159:1527-1562.
[12] Jilek P.Modeling and Inversion of Converted-Wave Reflection Coefficients in Anisotropic Media:A Tool for Quantitative AVO Analysis[D].Denver City:Colorado School of Mines,2002.
[13] Cui Jie,Han Li-guo,Liu Qian-kun,et al.P-SV Wave Elastic Impedance and Fluid Identification Factor in Weakly Anisotropic Media[J].Applied Geophysics,2010,7(2):135-142.
[14] 甘利灯,赵邦六,杜文辉,等.弹性阻抗在岩性与流体预测中的潜力分析[J].石油物探,2005,44(5):504-508.
Gan Li-deng,Zhao Bang-liu,Du Wen-hui,et al.The Potential Analysis of Elastic Impedance in the Lithology and Fluid Prediction[J].Geophysical Prospecting for Petroleum,2005,44(5):504-508.
[15] 李录明,罗省贤,王明春,等.各向异性介质三维纵横波联合叠前反演方法及应用[J].石油地球物理勘探,2010,11(1):164-170.
Li Lu-ming,Luo Sheng-xian,Wang Ming-chun,et al.3DPP-PS Joint Inversion Method and Application in Anisotropic Medium[J].Oil Geophysical Prospecting,2010,11(1):164-170.
[16] 王保丽,印兴耀,张繁昌,等.基于Fatti近似的弹性阻抗方程及反演[J].地球物理学进展,2008,23(1):192-197.
Wang Bao-li,Yin Xing-yao,Zhang Fan-chang,et al.Elastic Impedance Equation Based on Fatti Approximation and Inversion[J].Progress in Geophysics,2008,23(1):192-197.
[17] 喻岳钰,杨长春,王彦飞,等.叠前弹性阻抗反演及其在含气储层预测中的应用[J].地球物理学进展,2009,24(2):574-580.
Yu Yue-yu,Yang Chang-chun,Wang Yan-fei,et al.Application of Pre-Stack Seismic Elastic Impedance Inversion to Gas Reservoir[J].Progress in Geophysics,2009,24(2):574-580.
[18] 杨晓,王真理,喻岳钰.裂缝型储层地震检测方法综述[J].地球物理学进展,2010,25(5):1785-1794.
Yang Xiao,Wang Zhen-li,Yu Yue-yu.The Overview of Seismic Techniques in Prediction of Fracture Reservoir[J].Progress in Geophysics,2010,25(5):1785-1794.
[19] Bakulin A,Grechkaz V,Tsvankin I.Estimation of Fracture Parameters from Reflection Seismic Data:Part I:HTI Model due to a Single Fracture Set[J].Geophysics,2000,65(6):1788-1802.
[20] Hudson J A.Overall Properties of a Cracked Solid[J].Math Proc Camb Phil Soc,1980,88:371-384.
[21] Hudson J A.Wave Speeds and Attenuation of Elastic Waves in Material Containing Cracks[J].Geophy J Roy Astr Soc,1981,64:133-150.
[22] Schoenberg M.Elastic Wave Behavior Across Linear Slip Interfaces[J].J Acoust Soc Am,1980,68:1516-1521.
[23] Schoenberg M.Reflection of Elastic Waves from Periodically Stratified Media with Interfacial Slip[J].Geophysics Prosp,1983,31:265-292.
[24] Schoenberg M,Douma J.Elastic Wave Propagation in Media with Parallel Fractures and Aligned Cracks[J].Geophys Prosp,1988,36:571-590.
[25] Hudson J A.Seismic Wave Propagation Through Material Containing Partially Saturated Cracks[J].Geophy J,1988,92:33-37.
[26] Thomsen L.Elastic Anisotropy due to Aligned Cracks in Porous Rock[J].Geophysics Prospecting,1995,43:805-830.
[27] Hudson J A,Liu E,Crampin S.The Mechanical Properties of Materials with Interconnected Cracks and Pores[J].Geophys J Internat,1996,124:105-112.
[28] 王德利,何樵登,韩立国.裂隙型单斜介质中多方位地面三分量记录模拟[J].地球物理学报,2005,48(2):386-393.
Wang De-li,He Qiao-deng,Han Li-guo.Multi-Azimuth Three-Component Surface Seismic Modeling for Cracked Monoclinic Media[J].Chinese Journal of Geophysics,2005,48(2):386-393.
[29] Rüger A.P-Wave Reflection Coefficients for Transversely Isotropic Models with Vertical and Horizontal Axis of Symmetry[J].Geophysics,1997,62(3):713-722.
[30] Rüger A.Variation of P-Wave Reflectivity with Offset and Azimuth in Anisotropic Media[J].Geophysics,1998,63(3):935-947.
[31] Barnola A S,White R E.Gardner’s Relations and AVO Inversion[J].First Break,2001,19(11):607-611.
[32] Buia M,Flores Pablo E,Hill D,et al.Shooting Seismic Surveys in Circles[J].Oilfield Review,2008,20(3):18-31.
Elastic Impedance in Fractured HTI Media
Dou Xi-ying1,Han Li-guo1,Liu Chun-cheng2,Yang Xiao-chun2
1.College of GeoExploration Science &Technology,Jilin University,Changchun 130026,China 2.China Offshore Oil Corporation Research Institute,Beijing 100027,China
The fillings property and distribution density of cracks and vs/vpof wall rocks are introduced into P-wave and converted SV-wave elastic impedance equations in cracked horizontal transversely isotropic media,and normalization response characteristic of elastic impedance is simulated.The subsequent numerical simulation results show that elastic impedances in fractured media are azimuthally anisotropic and increase with the crack distribution densities;the range of elastic impedance for P-wave and converted SV-wave are in great differences;the elastic impedance differences may be considered as an identification of gas or water of crack fillings for the typical sandstones.
elastic impedance;cracks;fillings;crack density;vS/vP
book=2012,ebook=507
P631.4
A
1671-5888(2012) 04-1192-07
2011-11-14
国家科技重大专项项目(2011ZX05025-001-07)
窦喜英(1980-),女,博士研究生,主要从事储层预测与流体识别研究,E-mail:xiyingdou@163.com。

