可变模糊理论与模糊粗糙集在地下水污染评估中的应用
马 荣,石建省,刘继朝
中国地质科学院水文地质环境地质研究所,石家庄 050061
可变模糊理论与模糊粗糙集在地下水污染评估中的应用
马 荣,石建省,刘继朝
中国地质科学院水文地质环境地质研究所,石家庄 050061
传统的地下水污染评估方法需检测多项地下水化学变量,成本较高且无法考虑水质指标区间量值的影响。为此,笔者利用可变模糊理论对地下水污染进行综合评估,在此基础上通过模糊粗糙集理论挖掘关键变量,并利用生成的最小决策规则库对样品点的污染综合指数进行预测。将该方法应用于洛阳盆地,对其有效性进行验证,计算结果表明:As、Hg、Se、I、NH3-N对研究区地下水污染分类起控制作用。通过与实测的13种化学变量所计算的地下水污染综合指数相比,测试数据中7组样品的相对误差为0.104 0~0.172 5;剩余15组样品的相对误差为0.001 5~0.093 7,基本满足地下水污染评估的要求。可变模糊集与模糊粗糙集理论能够通过较少的化学变量对污染综合指数进行预测,从而降低地下水污染评估成本,为后续的地下水污染控制与修复提供可靠的数据来源。
地下水;化学变量;污染;模糊;误差
0 引言
近年来,地下水污染问题已引起人们的普遍关注,国内外许多学者对污染物在地下水中的运移[1-3]、控制和修复[4-8]等进行了大量研究。但上述研究均是建立在研究人员对地下水污染状况有着深刻认识基础之上的,如果没有大量实测的地下水化学变量数据,关于地下水污染研究的成果也难以令人满意[9];故在理论上应该对地下水体的所有化学组分进行检测,综合评定地下水的总体污染效果。但对某一地区而言,污染物往往集中在一项或几项指标上,如果对所有元素进行系统的测试与分析,不但浪费不必要的人力和物力,且使研究人员在后续的地下水污染防治中面临众多化学变量,从而增加计算量,有时甚至会使一些经典数值计算方法(如遗传算法和模拟退火算法等)的解在局部无法收敛[10-12]。
通过模糊粗糙集来挖掘对地下水污染分类起关键作用的化学变量,删除冗余属性,降低污染监测和计算成本,对地下水污染评估研究有重要意义。Dubois等[13]的研究表明,决策属性对于模糊粗糙集属性约简效率有重要影响,在本次研究中决策属性即为地下水污染综合指数。在地下水污染评估时,《地下水质量标准》[14]是重要的评估依据,但其对于各个化学变量的水质标准为区间形式的量值;而在传统的模糊综合评价中,模糊子集的隶属函数形式由研究人员选择确定,一般采用较简单的对称线性分布,如梯形、三角形和专家打分等,其分布函数所表示的隶属度都是论域中的变量隶属于某一化学变量标准点的隶属度[15],无法考虑水质指标区间形式的量值。因此应用现有的模糊子集分布函数来进行模糊综合评价是不合适的,需要研究一种基于标准区间值模糊子集分布函数的模糊评价方法。
基于以上原因,利用可变模糊理论对地下水污染进行综合评价,作为模糊粗糙集的决策属性。可变模糊理论的引入能够在地下水污染评估中充分利用地下水分类指标区间形式的量值来对地下水污染进行分类,建立关于各个不同区间相对隶属度的概念;该理论克服了传统隶属度在确定过程中基于某一标准点所建立的缺陷,在考虑多个水质标准区间的基础上对地下水污染进行综合评估。模糊粗糙集能够分析隐藏在数据中的事实而不需要关于数据的任何附加信息,具有较好的客观性和实用性等特点[16],故在建立相对隶属度矩阵的基础上可利用其在地下水化学变量和污染综合指数间建立最小决策规则库,挖掘出对地下水污染综合指数起控制作用的关键因子。地下水化学变量中关键因子的挖掘不仅可以显著减少地下水污染评估成本,且能够降低后续地下水污染控制与修复的计算成本。
1 理论方法
1.1 可变模糊理论
可变模糊集理论是建立在工程模糊集理论基础之上的,是一个比较系统的可变模糊集体系[17]。设论域U为研究区所有地下水样品的集合,模糊概念表示《地下水质量标准》[14]中某一水质分类等级。对U中的任意地下水样u,其在相对隶属函数的连续数轴任意点上对表示吸引性质A的相对隶属度为对表示排斥性质的槇相对隶属度为
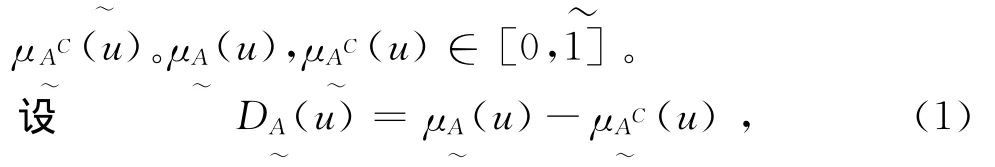
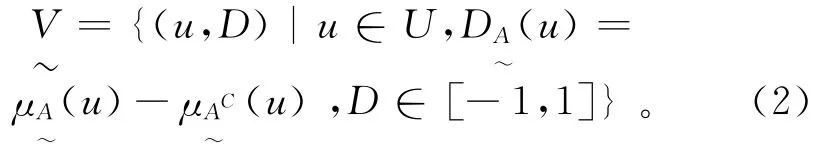
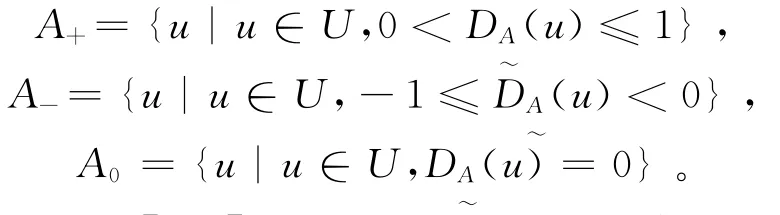
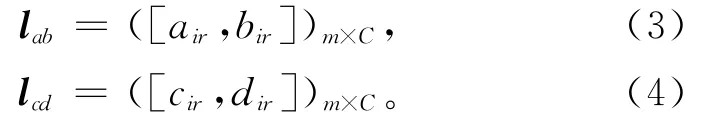
式中:i=1,2,…,m,m为地下水水质评价指标数;r=1,2,…,C;C为地下水水质的分类等级。点值矩阵Mir选取在区间[air,bir]中样品点相对于第r分类其隶属度等于1的值。
x为X区间内任意采样点评价指标的浓度值,则x落入M点左侧时的相对差异函数模型为x落入M点右侧时的相对差异函数模型为
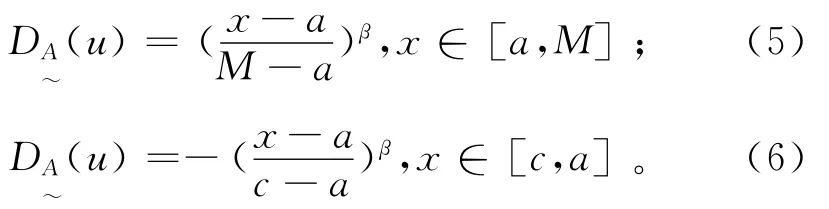
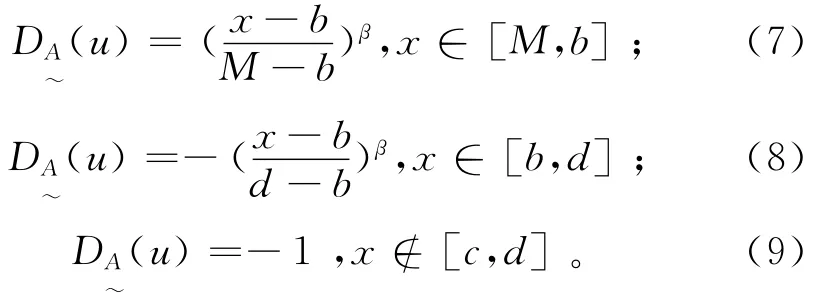
公式(5)-(7)中,β为非负指数。为了得到各指标的综合相对隶属度,应用如下公式构建可变模糊评价模型:
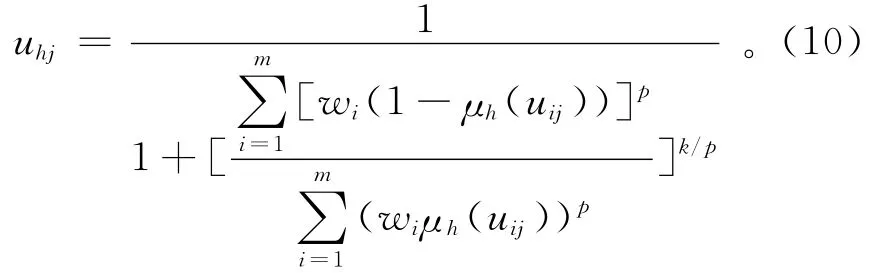
式中:uhj为综合隶属度;wi为指标权重;p为聚类参数;k为模型优化准则参数,k=1时优化准则为加权最小一乘方准则,k=2时优化准则为最小二乘方准则。公式中参数k和p可有4种组合:(k,p)={(1,1),(1,2),(2,1),(2,2)},在计算过程中,可以通过改变参数k和p进行模糊综合评判,以获得稳定的评价结果。
1.2 模糊粗糙集
在模糊粗糙集中,由于引入了模糊集合理论,条件属性和决策属性都可以是模糊的,属性对应的是相似关系,连续值属性的离散化过程被属性模糊化过程所代替,也就是将实数转化为相应的隶属度,因此能更客观地表达现实世界的模糊性和随机性[18]。模糊粗糙集属性约简方法在于把对象抽象成为一个模糊信息系统,表示为FIS=(U,T,E,V,f)。其中:U={x1,x2,x3,…,xn},是n个对象的非空有限集合,称为论域,xi=(hi1,hi2,…,hiq);T={T1,T2,…,Tq},是一组模糊条件属性,q为条件属性个数,属性Ti可表示为g个模糊语言项的集合FLTi={ti1,ti2,…,tij,…,tig}(1≤i≤q;1≤j≤g);E是一组模糊决策属性,可表示为s个模糊语言项的集合FLE={e1,e2,…,es};T和E均是U上的模糊划分[19],如公式(11)、(12)所示;,其中VTi(1≤i≤q)为属性集合的值域;f:U×T→为信息函数
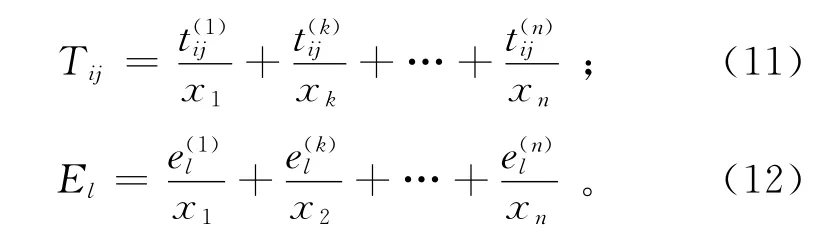
其中:tkij(1≤i≤q;1≤j≤g;1≤k≤n)为条件属性隶属度;e(k)l(1≤l≤s;1≤k≤n)为决策属性隶属度[20]。
设属性集T下的模糊等价关系为RT,属性集Q下的模糊等价关系为RQ,则属性集Q相对属性集T的条件熵定义为
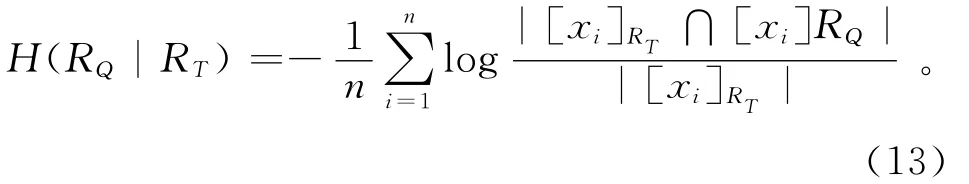
2 实例分析
在利用可变模糊理论耦合模糊粗糙集挖掘对地下水污染起控制作用的化学变量过程中,主要包括以下3个步骤:1)利用可变模糊理论对收集到的302组地下水化学样品进行模糊综合评价,并根据其综合指数进行污染等级分类,即模糊粗糙集的决策属性离散化;2)利用模糊粗糙集理论中的信息熵约简算法挖掘对地下水污染分类起控制作用的化学变量,从而在地下水化学变量与污染综合指数间建立决策规则库;3)根据训练好的决策规则库对测试数据的地下水污染综合指数进行预测,并对其进行误差分析,来验证本文所提出的新方法的有效性。
2.1 研究区概况
洛阳盆地总面积达5 360km2,地势西高东低,南北高中间低,由中心至周边,地形逐次升高,且整体由西向东倾斜。伊洛河冲积平原区浅层地下水埋藏浅,水量丰富,洛阳及郑州市生活及工农业用水多以开采盆地内浅层地下水为主。研究区共采集了浅层地下水样品302组(图1),检测了28项地下水化学变量,其中包括Mn、Fe、Cu、Zn、Ba、K、Ni、Be、Co、Cd、Pb、As、Hg、Se、NO3、F、Mo、Cl、NO2、CN、Cr、PO4、I、NH3-N、化学需氧量(chemical oxygen demand,COD)、溶解性总固体(total dissolved solids,TDS)的质量浓度,总硬度(total hardness,TH)和pH。所有样品均由中国地质科学院水文地质测试中心完成。在本次研究中,样品的采集与测试是进行分析研究的关键,根据研究区的实际情况,依据《地下水污染调查评价规范》[22]和美国环境保护局的《地下水水样采集要求》[23]制定了污染物分析水样的采集、保存和送检技术要求。其中电导率(electrical conductivity,EC)、温度和pH均在现场测试完成,原水样均用2.5L聚乙烯塑料瓶装样,体积达到容器的99%,不加保护剂。为保证最终检测结果的准确性与有效性,在所有的采样点每次均取2个样品进行测试研究。
2.2 数据准备
本次研究共采集302组浅层地下水化学样品,检测28项化学变量,但由于Mn、Cu和K等离子的质量浓度远低于《地下水质量标准》[14]中的二类水水质标准,且其在整个研究区的质量浓度分布较为均一,对地下水污染分类无明显影响,故在本文中只选取Ba、As、Hg、Se、NO3、F、COD、I、TH、TDS、NH3-N、pH和Fe离子13种化学变量作为模糊粗糙集的条件属性集;通过可变模糊理论对302组水化学样品进行综合评价,并根据其污染综合指数进行分类,作为模糊粗糙集的决策属性。在此基础上,将收集到的地下水化学样品分为2组:选取其中的280组样品为训练数据,构建决策规则库;将剩余的22组样品作为测试数据,利用其对决策规则库进行检测,来验证该方法的有效性。
2.3 地下水污染综合评价
对研究区302组地下水化学样品进行统计分析,并结合《地下水质量标准》[14],利用可变模糊理论对样品点进行综合评价,详细计算过程如下:
1)根据式(1)-(3)建立地下水污染评价可变集合的吸引域矩阵lab、范围域矩阵lcd(表1,2)以及点
2)利用lab、lcd和Mir判断样本特征值xij在M点的左侧还是右侧,据此选择公式(5)、(6)或公式(7)、(8)计算水质样本对每个指标的相对差异度和相对隶属度,并利用熵权法[25]求得上述13个化学变量的权值:
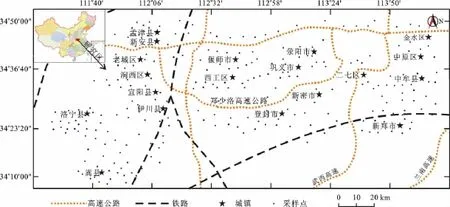
图1 研究区及采样分布图Fig.1 Study area and sample location
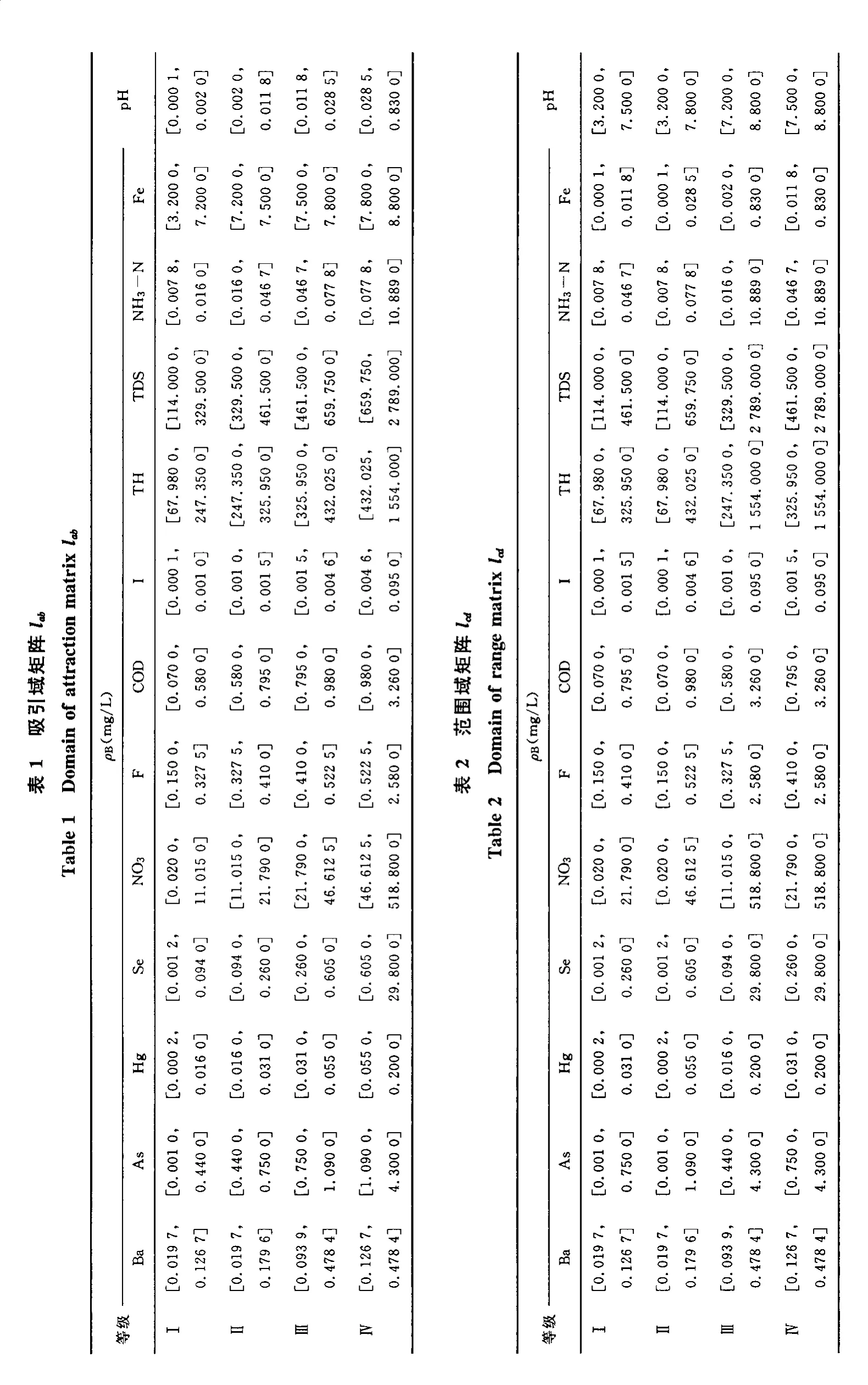
wi={0.070 0,0.070 7,0.071 1,0.084 1,0.075 7,0.070 9,0.069 8,0.090 0,0.069 8,0.070 6,0.103 2,0.068 2,0.085 9},由公式(10),分别采用{k=1,p=1;k=1,p=2;k=2,p=1;k=2,p=2}4种参数变换模型计算各个样品的地下水污染综合指数,结合洛阳盆地水文地质条件与水化学背景对综合指数进行分类,为模糊粗糙集提供决策属性(表3)。
2.4 建立决策规则库
在本文所构建的模糊信息系统决策表中,条件属性集为ρ(Ba)、ρ(As)和ρ(Hg)等13种化学变量;决策属性集E为地下水污染综合指数。其中条件属性为模糊值,取值{μ11,μ12}表示达到第Ⅲ类水质标准的隶属度为μ11,未达到第Ⅲ类水质标准的隶属度为μ12,依次建立13种地下水化学变量的模糊值。
在建立模糊信息系统决策表的基础上,利用信息熵求取该决策表的最小属性约简,挖掘对研究区地下水污染分类起控制作用的化学变量,具体的计算过程如下。
1)对每条属性利用Extended Jaccarad量度计算对象间的模糊相似度,从而建立模糊相似矩阵[26],在此基础上利用传递闭包法计算出各个条件属性的模糊等价矩阵。
2)令y=T,根据公式(13)计算条件属性集y相对决策属性集E的信息熵:H(RE|Ry)=1.994 4。
3)对条件属性集中每一条属性Ti(i=1,2,…,13),计算其相对决策属性E的条件信息熵:
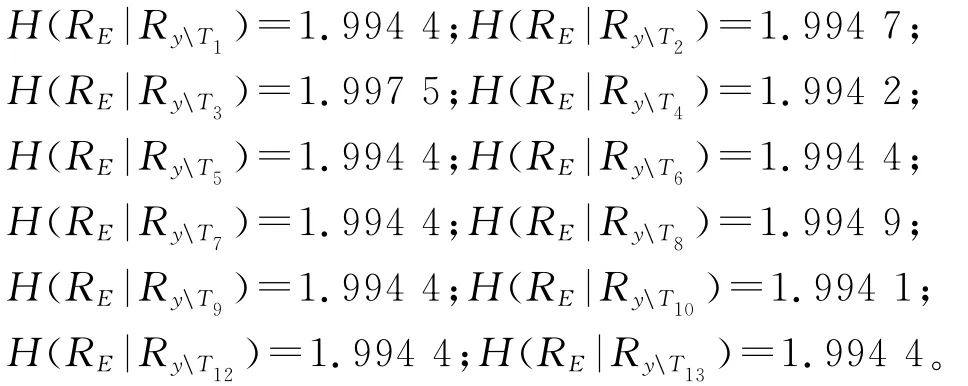
4)若H(RE|Ry)=H(RE|Ry\Ti),说明属性Ti相对决策属性E是不必要的,删除属性Ti所在的列,并将重复的行进行合并,且令y=y\Ti。
5)重复步骤3),直到条件属性集合不再发生变化为止,求得本次研究的模糊信息系统决策表的最小约简为{ρ(As),ρ(Hg),ρ(Se),ρ(I),ρ(NH3-N)},由上述5种化学变量归纳出的规则即为地下水污染分类的决策规则库(表4)。
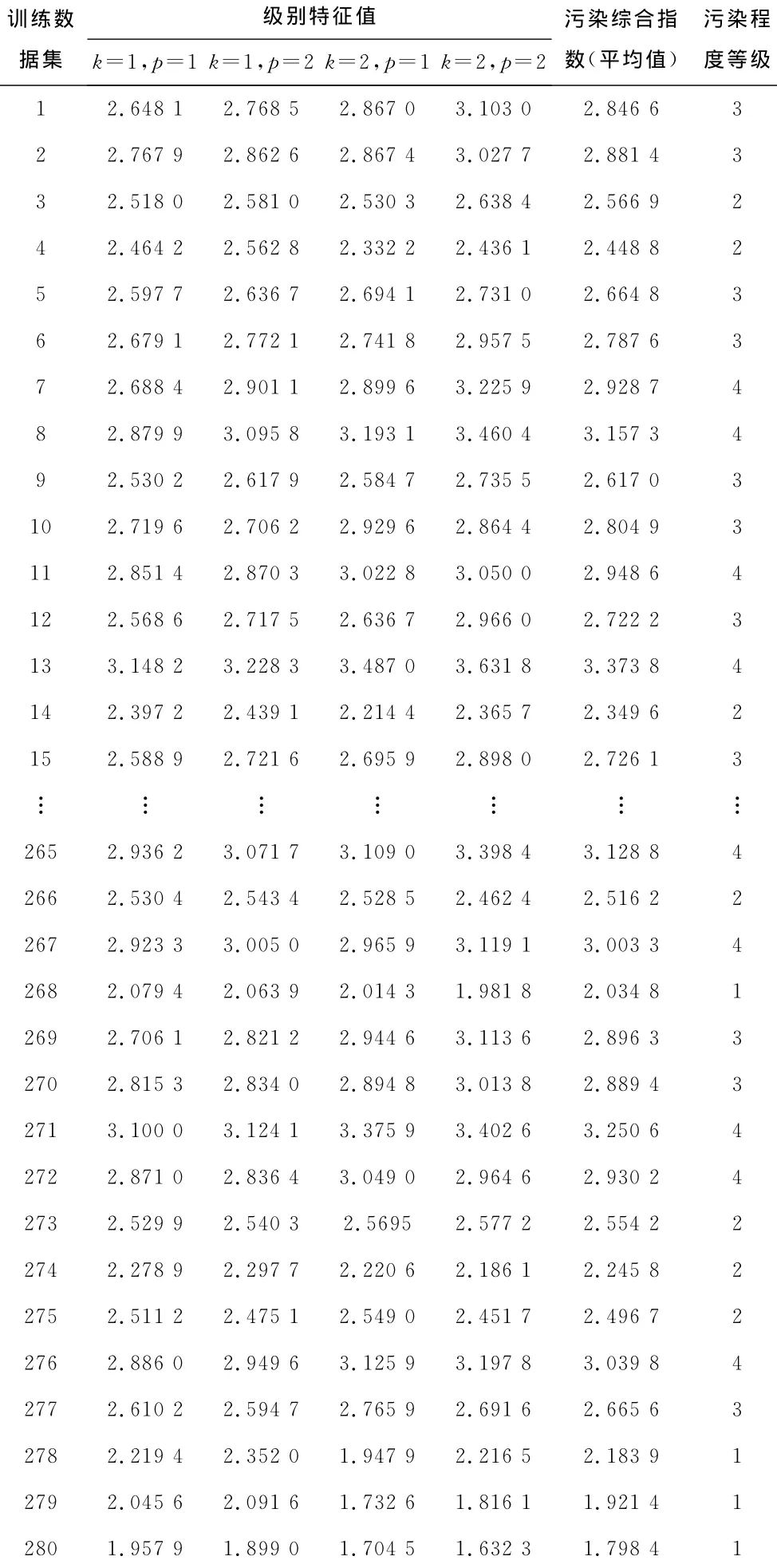
表3 地下水污染综合评价结果Table 3 Comprehensive evaluation results of groundwater pollution
2.5 规则测试
将测试数据中的22组水质分析样品带入上述的决策规则集中预测其相对应的污染综合指数。在本次计算中,共获取265条决策规则,为了能够在预测过程中充分应用所有的决策规则,利用模糊推理技术对测试数据进行预测[27]。以测试数据集中1号样品为例,其具体的计算过程如下。
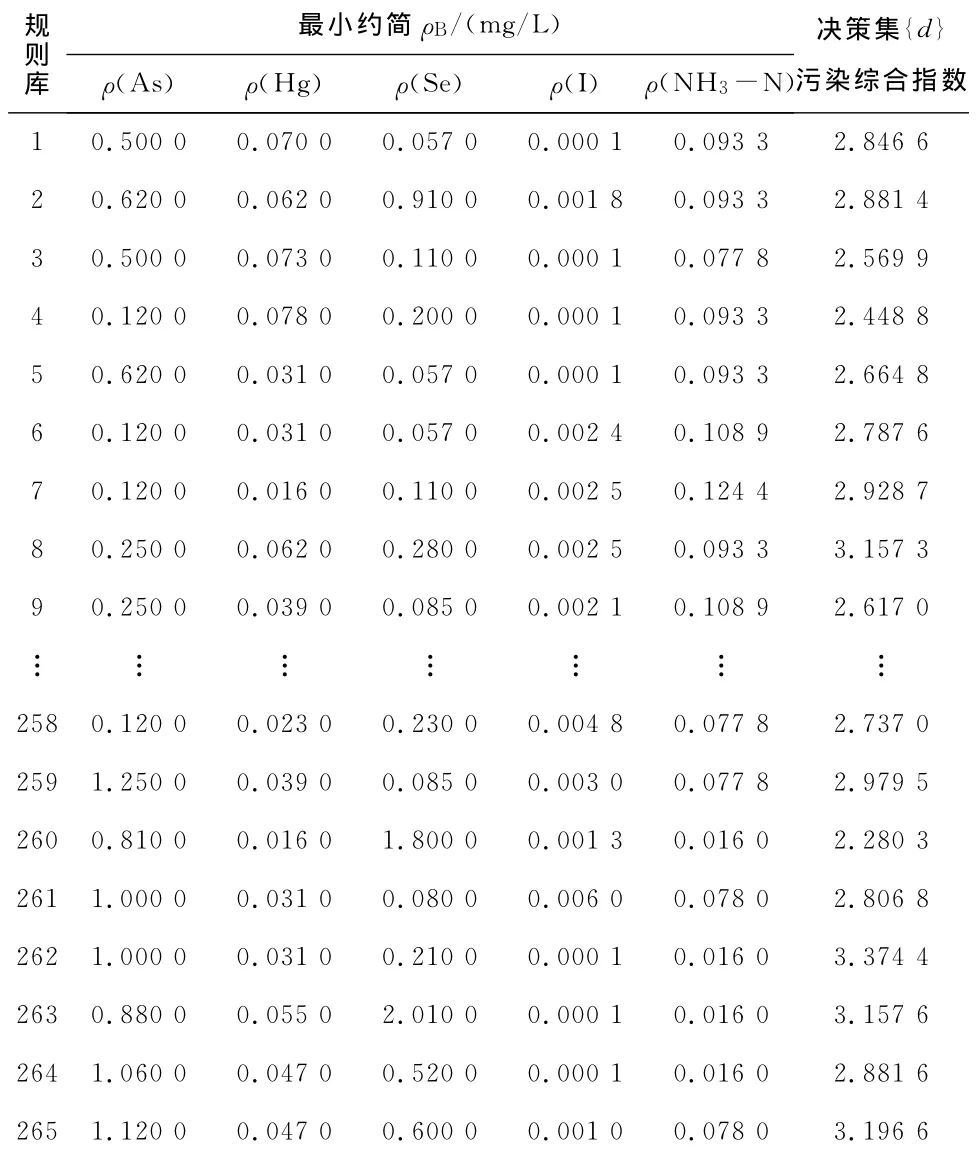
表4 地下水污染决策规则库Table 4 Decision rule database of groundwater pollution
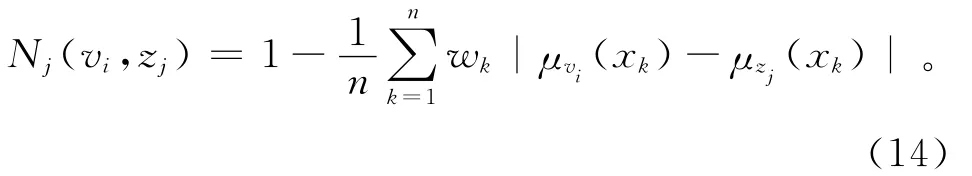
式中:vi(i=1,2,…,22)为测试数据;zj(j=1,2,…,265)为模糊粗糙集的决策规则;n为参与计算的5个化学变量;wk为各化学变量的权重,在本文中,主要根据其在模糊粗糙集中相对于决策属性E的信息熵计算而得。
2)在求得1号样品点与各决策规则贴近度的基础上,将其作为权系数,带入公式(15)即可求得样品点处的地下水污染综合指数:1)利用公式(14)计算出1号样品与上述最小决策规则库中各规则的海明贴近度:

式中:i=1,2,…,22为测试样品号;Ej(j=1,2,…,265)为各决策规则所对应的污染综合指数。
根据此方法即可求出测试数据中22组地下水样品的污染综合指数(表5)。

表5 测试数据中地下水污染综合指数Table 5 Prediction value of groundwater pollution synthetic index in testing data
通过可变模糊理论对洛阳盆地地下水污染进行综合评价,污染综合指数为1.521 7~3.606 7(表3中省略了部分数据),其中洛阳市涧西区地下水污染综合指数较高,这主要是由于该区集中了洛阳市主要的工矿企业,污染较为严重;这表明可变模糊理论能够真实刻画地下水污染状况。在此基础上利用模糊粗糙集理论,挖掘对研究区地下水污染分类起控制作用的5个化学变量(ρ(As)、ρ(Hg)、ρ(Se)、ρ(I)、ρ(NH3-N)),并构建出265条决策规则,通过上述的最小决策规则对测试数据集中地下水化学样品的综合指数进行预测,预测值为1.557 9~3.916 6;通过与实测的13种化学变量所计算的地下水污染综合指数相比,其中7组样品(1、2、5、7、8、11、15、22)的相对误差为0.104 0~0.183 9,剩余15组样品的相对误差为0.001 5~0.093 7(表5),计算结果基本令人满意。故基于可变模糊集与模糊粗糙集理论可以应用于实际的地下水污染评估。
3 结论
1)将可变模糊理论应用于洛阳盆地地下水污染综合评估中,通过相对隶属度函数的引入,在评估过程中充分考虑不同水质标准区间量值的影响,从而使得地下水污染评估更加科学与准确,为后续的模糊粗糙集理论提供良好的决策属性,在一定程度上保证了本次研究具有较高的计算精度。
2)地下水污染综合评估是后续地下水污染运移、控制与修复研究的基础,通过模糊粗糙集理论,只需检测洛阳盆地地下水中5种化学变量即可求得任意点处的污染综合指数;这极大地降低了地下水污染评估成本,使研究人员能够在有限的时间与资金内获取更多的监测数据,从而为后续的污染研究提供可靠的数据支撑。
(References):
[1] 姜桂华,王文科,乔小英,等.关中盆地地下水特殊脆弱性及其评价[J].吉林大学学报:地球科学版,2009,39(6):1107-1110.
Jiang Gui-hua,Wang Wen-ke,Qiao Xiao-ying,et al.Groundwater Special Vulnerability and Its Assessment in Guanzhong Basin[J].Journal of Jilin University:Earth Science Edition,2009,39(6):1107-1110.
[2] 马荣,石建省.模糊因子分析在地下水污染评估中的应用:以河南省洛阳市为例[J].地球学报,2011,32(5):611-622.
Ma Rong,Shi Jian-sheng.Assessing Groundwater Pollution Using Fuzzy Factor Analysis Method:A Case Study of Luoyang City in Henan Province[J].Acta Geoscientica Sinica,2011,32(5):611-622.
[3] Ma R,Zheng C,Tonkin M J,et al.Importance of Considering Intraborehole Flow in Solute Transport Modeling Under Highly Dynamic Flow Conditions[J].Journal of Contaminant Hydrology,2011,123(1/2):11-19.
[4] 梁博,王晓燕.我国水环所污染物总量控制研究的现状与展望[J].首都师范大学学报:自然科学版,2005,26(1):93-98.
Liang Bo,Wang Xiao-yan.The Current Situation and Expectation of Our Country Water Environment Contamination Gross Control[J].Journal of Capital Normal University:Natural Science Edition,2005,26(1):93-98.
[5] 张维理,徐爱国,冀宏杰,等.中国农业面源污染形式估计及控制对策:Ⅲ:中国农业面源污染控制中存在问题分析[J].中国农业科学,2004,37(7):1026-1033.
Zhang Wei-li,Xu Ai-guo,Ji Hong-jie,et al.Estimation of Agricultural Non-Point Source Pollution in China and the Alleviating Strategies:Ⅲ:A Review of Policies and Practices for Agricultural Non-Point Source Pollution Control in China[J].Scientia Agricultura Sinica,2004,37(7):1026-1033.
[6] 曹泉,王兴润.铬渣污染场地污染状况研究与修复技术[J].环境工程学报,2009,3(8):1493-1497.
Cao Quan,Wang Xing-run.Study on Pollution Characteristics of Contaminated Sites with Chrome and Discussion on Common Remediation Technologies[J].Chinese Journal of Environmental Engineering,2009,3(8):1493-1497.
[7] 赵勇胜.地下水污染场地污染的控制与修复[J].吉林大学学报:地球科学版,2007,37(2):303-310.
Zhao Yong-sheng.Groundwater Pollution Control and Remediation[J].Journal of Jilin University:Earth Science Edition,2007,37(2):303-310.
[8] 崔俊芳,郑西来,林国庆.地下水有机污染处理的渗透性反应墙技术[J].水科学进展,2003,14(3):363-367.
Cui Jun-fang,Zheng Xi-lai,Lin Guo-qing.Permeable Reactive Wall for Remediation of Organic-Contaminated Groundwater[J].Advances in Water Sciences,2003,14(3):363-367.
[9] Stamatis G,Parpodis K,Filintas A,et al.Groundwater Quality,Nitrate Pollution and Irrigation Environmental Management in the Neogene Sediments of an Agricultural Region in Central Thessaly(Greece)[J].Environ Earth Sci,2011,64(4):1081-1105.
[10] Botalova O,Schwarzbauer J.Geochemical Characterization of Organic Pollutants in Effluents Discharged from Various Industrial Sources to Riverine Systems[J].Water,Air,&Soil Pollution,2011,217(1/2/3/4):1-22.
[11] 姚磊华,李竞生.综合改进的遗传算法反演三维地下水流模型参数[J].岩石力学与工程学报,2004,23(4):625-630.
Yao Lei-hua,Li Jing-sheng.Parameter Identification of 3DGroundwater Flow Model with Improved Genetic Alorithm[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(4):625-630.
[12] 邵立南,刘志斌.模拟退火神经网络模型在地下水质评价中应用[J].辽宁工程技术大学学报,2005,24(增刊1):152-158.
Shao Li-nan,Liu Zhi-bin.Application of SA-BP Model in Appraising Groundwater Quality[J].Jour-nal of Liaoning Technical University,2005,24(Sup.1):152-158.
[13] Dubois D,Prade H.Rough Fuzzy Sets and Fuzzy Rough Sets[J].Int J Gen Syst,1990,17(2/3):191-209.
[14] GB/T 14848-93地下水质量标准[S].北京:中国地质调查局,1994.
GB/T 14848-93Quality Standard for Ground Water[S].Beijing:China Geological Survey,1994.
[15] Tutmez B,Tercan A E,Kaymak U.Fuzzy Modeling for Reserve Estimation Based on Spatial Variability[J].Mathematical Geology,2007,39(1):97-111.
[16] Shang C,Barnes D,Shen Q.Fuzzy-Rough Set Feature Selection for Mars Terrain Image Classification[J].Intelligent Systems Design and Applications,2009,9(3):1419-1424.
[17] 陈守煜.工程可变模糊集理论与模型:模糊水文水资源学数学基础[J].大连理工大学学报,2005,42(2):308-312.
Chen Shou-yu.Theory and Model of Engineering Variable Fuzzy Set:Mathematical Basis for Fuzzy Hydrology and Water Resource[J].Journal of Dalian University of Technology,2005,42(2):308-312.
[18] Pawlak Z.Rough Set[J].Int J Comput Inform Sci,1982,11(5):341-356.
[19] Chen S M,Tsai F M.Generating Fuzzy Rules from Training Instances for Fuzzy Classification Systems[J].Expert Syst Appl,2008,35(3):611-621.
[20] Jensen R,Shen Q.Semantics-Preserving Dimensionality Reduction:Rough and Fuzzy-Rough-Based Approaches[J].IEEE Transactions on Knowledge and Data Engineering,2004,16(12):1457-1471.
[21] Hu Qing-hua,Yu Da-ren,Xie Zong-xia,et al.Fuzzy Probabilistic Approximation Spaces and Their Information Measures[J].IEEE Transaction on Fuzzy System,2006,14(2):191-201.
[22] DD2008-01地下水污染调查评价规范(1∶50 000-1∶250 000)[S].北京:中国地质调查局,2008.DD2008-01Groundwater Pollution Investigation Evaluation Norm(1∶50 000-1∶250 000)[S].Beijing:China Geological Survey,2008.
[23] 540/S-95/504-1996Low-Flow(Minimal Drawdown)Groundwater Sampling Procedures[S].Washington:United States Environmental Protection Agency,1996.
[24] 陈守煜,李敏.基于可变模糊集理论的水资源可再生能力评价模型[J].水利学报,2006,37(4):431-435.
Chen Shou-yu,Li Min.Assessment Model of Water Resources Reproducible Ability Based on Variable Fuzzy Set Theory[J].Journal of Hydraulic Engineering,2006,37(4):431-435.
[25] Sharma L P,Nilanchal P,Ghose M K,et al.Influences of Shannon’s Entropy on Landslide-Causing Parameters for Vulnerability Study and Zonation:A Case Study in Sikkim,India[J].Arba J Geosci,2010,3(3):1-11.
[26] Kwang H L,Song Y S,Lee K M.Similarity Measure Between Fuzzy Sets and Between Elements[J].Fuzzy Sets and System,1994,62(3):291-293.
[27] Kholghi M,Hosseini S M.Comparison of Groundwater Level Estimation Using Neuro-Fuzzy and Ordinary Kriging[J].Environ Model Assess,2009,14(6):729-737.
Application of Variable Fuzzy Set Theory and Fuzzy-Rough Set to Groundwater Pollution Assessment
Ma Rong,Shi Jian-sheng,Liu Ji-chao
The Institute of Hydrogeology and Environmental Geology,Shijiazhuang 050061,China
Many hydrochemical variables were required to test in tradition methods in order to assess groundwater pollution,the cost was higher.More importantly,these methods could not consider the effect of interval water quality target limit on synthesis assessment.A new method was introduced in this paper:first the variable fuzzy set theory was employed to assess groundwater pollution;and then application of fuzzy rough set to evacuate critical variable,the min-decision rules were used to forecast groundwater pollution synthesis index,which was yield by fuzzy-rough set.This method was applied in Luoyang basin to evaluate its validity,the result indicated:there were five hydrochemical variables(As,Hg,Se,I,NH3-N)played a controlled role in groundwater pollution classification.In testing data,7 groups of samples'relative error was 0.104 0-0.172 5;the surplus 15groups samples’relative error was 0.001 5-0.093 7.Therefore,the groundwater pollution synthesis index could be predicted by variable fuzzy sets and fuzzy-rough set theory according to the above five hydrochemical variables,which could make the monitoring cost decrease and provide reliable data source for groundwater pollution control andremediation.
groundwater;hydrochemical variable;pollution;fuzzy;errors
book=2012,ebook=541
P641
A
1671-5888(2012) 04-1130-09
2011-10-25
国家“973”计划项目(2010CB428800)
马荣(1982-),男,博士,主要从事地下水污染方面的研究,E-mail:margroundwater@gmail.com
石建省(1962-),男,研究员,主要从事水文地质评价方面的研究,E-mail:tiger7886@263.net。

